вопросы по метре. Основные понятия метрологии. Классификация измерений и средств измерений. Принципы и методы измерений
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
Распределение Коши. 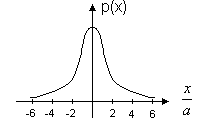 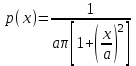 Это распределение близко к предельному пологому, т.е. для него выполняется условие 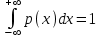 . .Распределение Лапласа (двустороннее экспоненциальное). 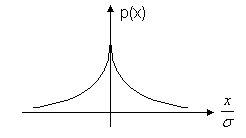 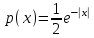 Наиболее часто используемое на практике и в теории вероятностей – нормальное распределение (распределение Гаусса). 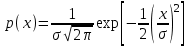 Т.е. по мере удаления от х=0 функция спадает быстрее, чем распределение Лапласа. 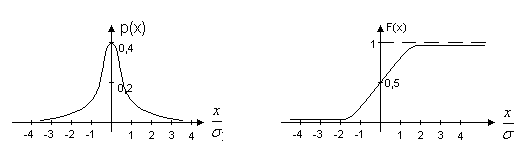 Применяется для большего числа наблюдений n. Если непрерывная случайная величина принимает значения лишь в пределах некоторого конечного интервала значений (x1, x2) с постоянной плотностью вероятностей, то такой закон распределения называется равномерным. Мат.ожидание нах-ся в центре. 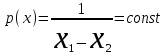 при x1 <x<x2 и при x1 <x<x2 и 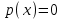 при x<x1 и x>x2 при x<x1 и x>x2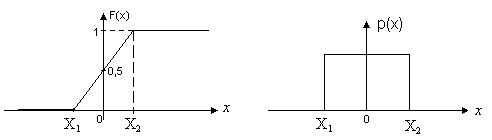 Распределение, при котором встречаются с равными вероятностями только два дискретных значения случайной величины +а и –а, называется дискретным двузначным распределением: 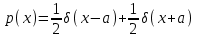 , ,г 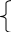 де де 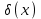 - дельта – функция Дирака, для которой: - дельта – функция Дирака, для которой:0, при t ≠ 0 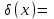 ∞, при t = 0 Распределение отсчетов синусоидально изменяющейся во времени величины x=xmsinωt, если моменты этих отсчетов равномерно распределены во времени, то оно называется арксинусоидальным(когда накладывается синус.помеха) Распределение Стьюдента (псевдоним Госсета, предсказавшего это распределение) наиболее часто применяется в процессе обработки результатов небольшого числа (2 ≤ 4 < 20) наблюдений случайной величины и справедлив, когда случайные погрешности распределены по нормальному закону. Для него вводится случайная величина: 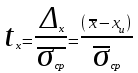 , ,где 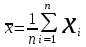 - оценка средней арифметической хi - оценка средней арифметической хi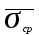 - оценка СКО случайной величины - оценка СКО случайной величины 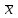 . .С ростом n (когда n→20) распределение Стьюдента быстро приближается к нормальному и тем значительнее отличается от него, чем меньше n. Отличия состоят в увеличении рассеяния относительных погрешностей tx относительно центра tx=0 при уменьшении числа наблюдений. Центральная предельная теорема *Если случайный процесс порожден некоторым кол-ом случайных величин, то закон распределения стремится к нормальному з-ну распределения. *Центральная предельная теорема показывает, что в случае, когда результат измерения (наблюдения) складывается под действием многих причин, причем каждая из них вносит лишь малый вклад, а совокупный итог определяется аддитивно, т.е. путем сложения, то распределение результата измерения (наблюдения) близко к нормальному. Вероятность попадания случайной величины X, распределенной по нормальному закону, в интервал [ 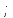 ], равна: ], равна: 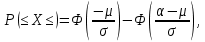 где где 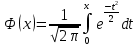 – функция Лапласа. Функция Лапласа нечетная: Ф(-x) = - Ф(х), – функция Лапласа. Функция Лапласа нечетная: Ф(-x) = - Ф(х),7. Прямые однократные и многократные измерения и их погрешности. Погрешности косвенных измерений. Многократные измерения Необходимость в многократных наблюдениях некоторой физической величины возникает при наличии в процессе измерений значительных случайных погрешностей. При этом задача обработки состоит в том, чтобы по результатам наблюдений определить наилучшую (оптимальную) оценку измеряемой величины и интервал, в котором она находится с заданной вероятностью. Данная задача может быть решена способом статистической обработки результатов наблюдений, основанным на гипотезе о распределении погрешностей результатов по нормальному закону. Итак, рассмотрим группу из n независимых результатов наблюдений случайной величины x, подчиняющейся нормальному распределению. Оценка рассеяния единичных результатов наблюдений в группе относительно их среднего значения вычисляется по формуле: 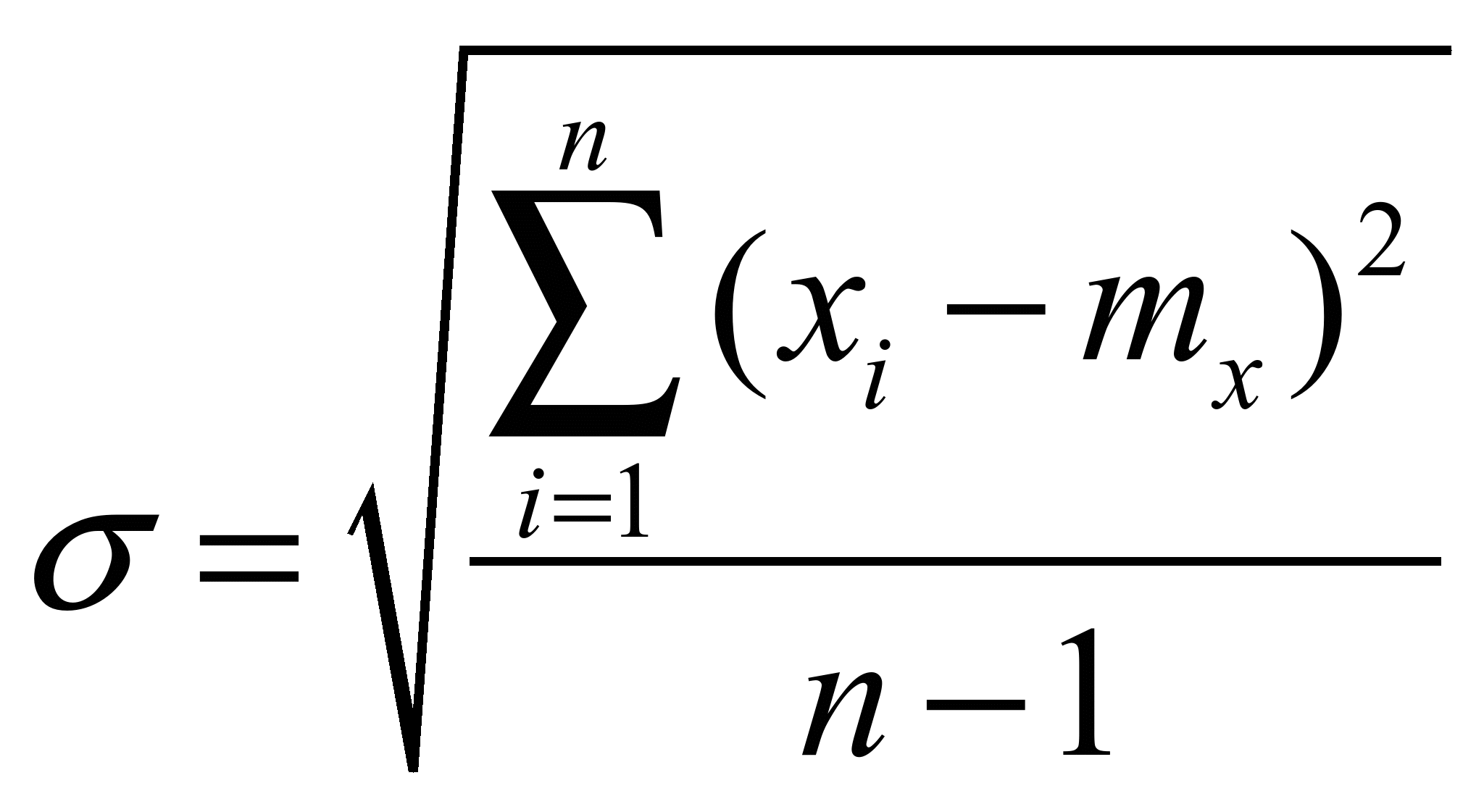 Поскольку число наблюдений в группе, на основании результатов которых выполнено вычисление среднего арифметического, ограничено, то, повторив заново серию наблюдений этой же величины, мы получили бы новое значение среднего арифметического. Повторив многократно наблюдения и вычисляя каждый раз их среднее арифметическое значение, принимаемое за результат наблюдений (измерений), обнаружим рассеяние среднего арифметического значения. Характеристикой этого рассеяния является средний квадрат отклонения среднего арифметического: 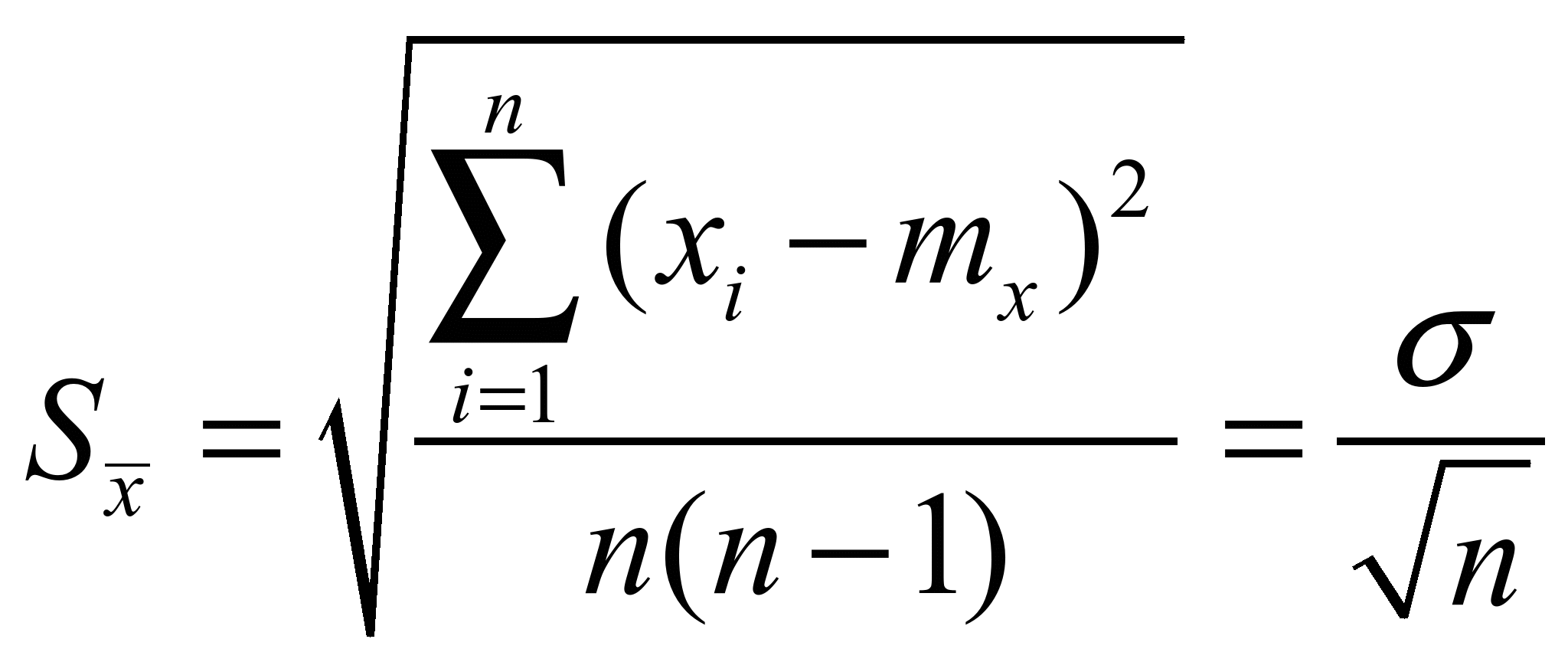 Теория показывает, что если рассеяние результатов наблюдения в группе подчиняется нормальному закону, то и их среднее арифметическое тоже подчиняется нормальному закону распределения при достаточно большом числе наблюдений (n>50). Отсюда при одинаковой доверительной вероятности доверительный интервал среднего арифметического в При нормальном законе распределения плотности вероятностей результатов наблюдений и небольшом числе измерений среднее арифметическое подчиняется закону распределения Стьюдента с тем же средним арифметическим Коэффициент распределения Стьюдента зависит от числа наблюдений и выбранной доверительной вероятности и находится по таблице. Обработка результатов наблюдения производится в следующей последовательности: 1)Исключить известные систематические погрешности из результатов наблюдения (введением поправки); 2)Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат наблюдений: 3)Вычислить оценку среднего квадратичного отклонения результата наблюдения: целесообразно проверить наличие в группе наблюдений грубых погрешностей, помня, что при нормальном законе распределения ни одна случайная погрешность , с вероятностью, практически равной 1, не может выйти за пределы ъ. Наблюдения, содержащие грубые погрешности, исключают из группы и заново повторяют вычисления. 4) Вычислить оценку среднего квадратичного отклонения среднего арифметического 5) Проверить гипотезу о том, что результаты измерений принадлежат нормальному распределению. Приближенно о характере распределения можно судить, построив гистограмму. Существуют и строгие методы проверки гипотез о том или ином характере распределения случайной величины. При числе наблюдений n<15 принадлежность их к нормальному распределению не проверяют, а доверительные границы случайной погрешности результата определяют лишь в том случае, если достоверно известно, что результаты наблюдений принадлежат нормальному закону. 6) Вычислить доверительные границы случайной погрешности результата измерения при заданной вероятности P. 7) Вычислить границы суммарной неисключенной систематической погрешности (НСП) результата измерения. НСП результата измерений образуется из неисключенных остатков измерений, погрешностей, поправок и т. д. При суммировании эти составляющие рассматриваются как случайные величины. При отсутствии данных о виде распределений НСП, их распределения принимают за равномерные. При равномерном распределении НСП границы НСП вычисляют по формуле: 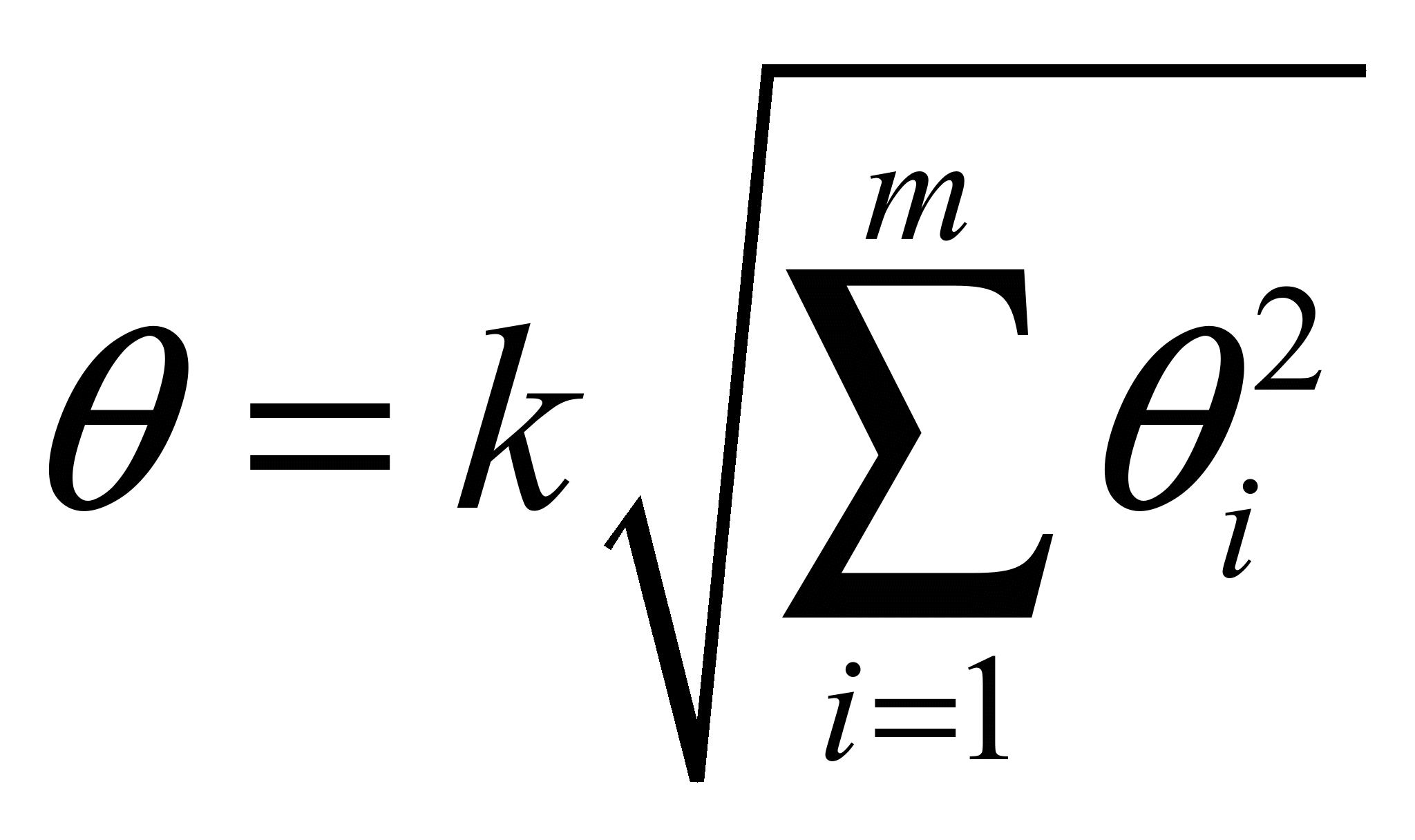 8) Вычислить доверительные границы погрешности результата измерения 9) Записать результат измерения в регламентированной стандартом форме. Однократные измерения Такой вид измерений является наиболее распространенным, когда речь идет о механических измерениях или физическом эксперименте. Однако они возможны лишь при следующих условиях: объем априорной информации об объекте измерений такой, что аналитическая модель объекта и измеряемой величины не вызывают сомнений; метод измерения достаточно изучен, и его погрешности либо заранее устранены, либо оценены; средства измерения исправны, а их метрологические характеристики соответствуют установленным нормам; применение методики обработки результатов прямых однократных измерений возможно, если известны составляющие погрешности измерения; закон распределения случайных составляющих - нормальный, а НСП – равномерный с известными границами. Результатом прямого однократного измерения физической величины является показание, снятое непосредственно с используемого средства измерения. До измерения должна быть проведена априорная оценка составляющих погрешности с использованием всех доступных данных. При определении доверительных границ погрешности результата измерений доверительная вероятность принимается равной 0,95. Погрешность результата прямого однократного измерения включает в себя погрешность средства измерения, методы измерения и субъективную погрешность оператора (которую можно легко устранить, применив цифровой прибор, но возникнет погрешность дискретизации). Любая из этих составляющих может иметь и НСП, и случайные составляющие. Оценивание погрешностей прямых однократных измерений можно подразделить на точное и приближенное. Методика точной оценки: 1) пусть число НСП m и каждая из них задана либо границами а во втором случае: 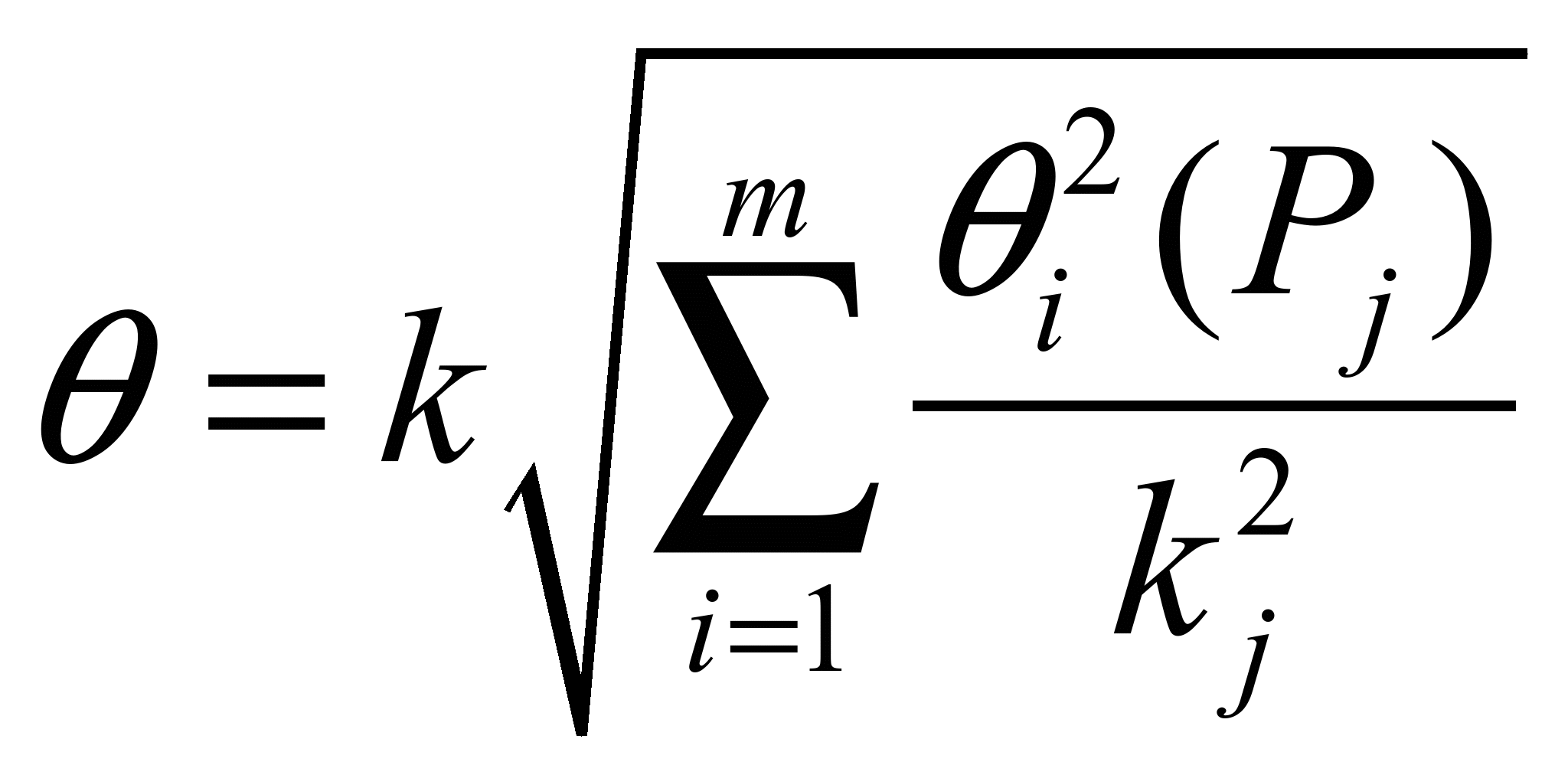 2) Если составляющие случайной погрешностей заданы их СКО, найденными предварительно опытным путем многократных наблюдений, то доверительные границы 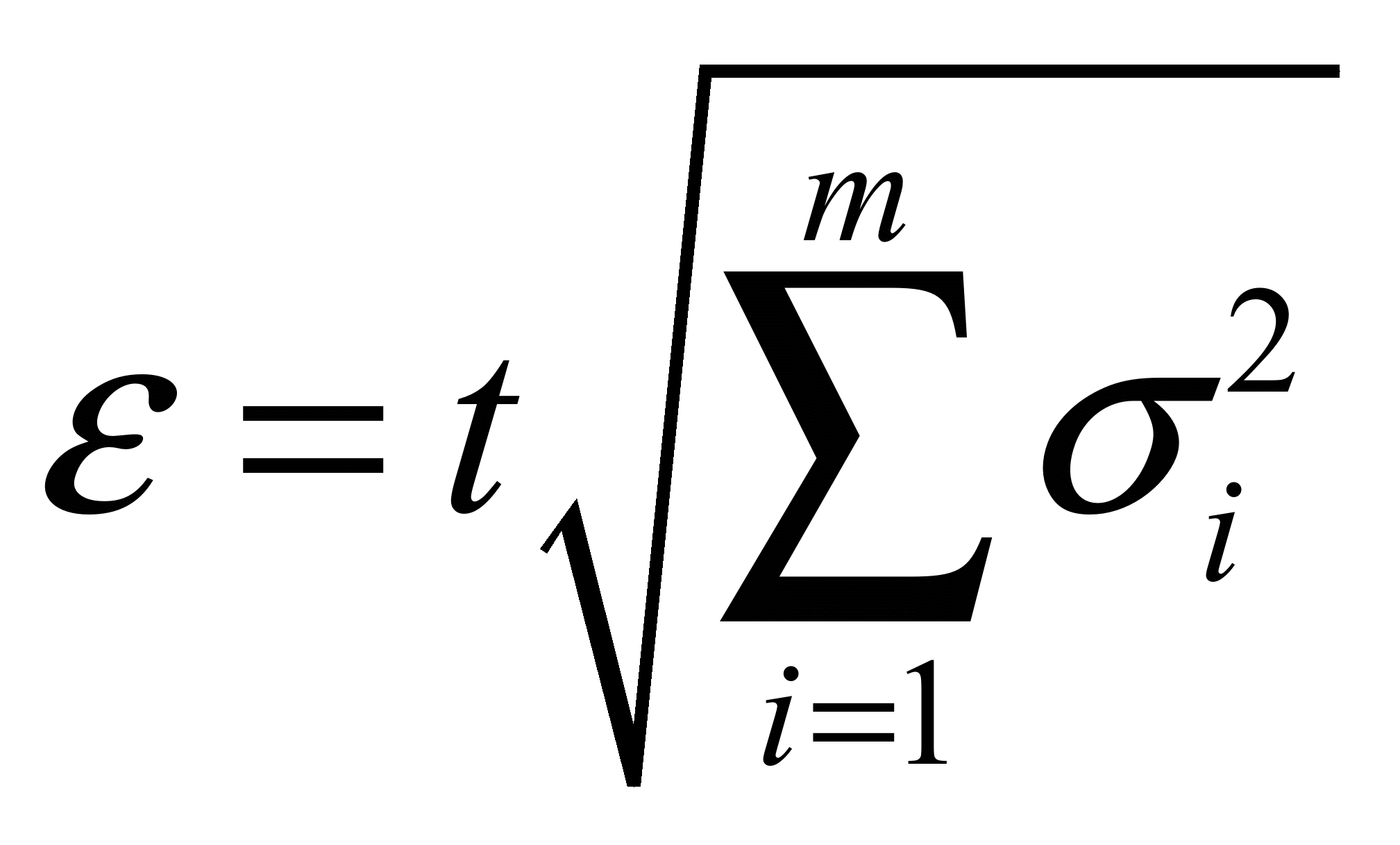 где t = 1,1 или можно брать коэффициент Стьюдента, соответствующий меньшему числу наблюдений. Если же случайные составляющие погрешности заданы доверительными границами 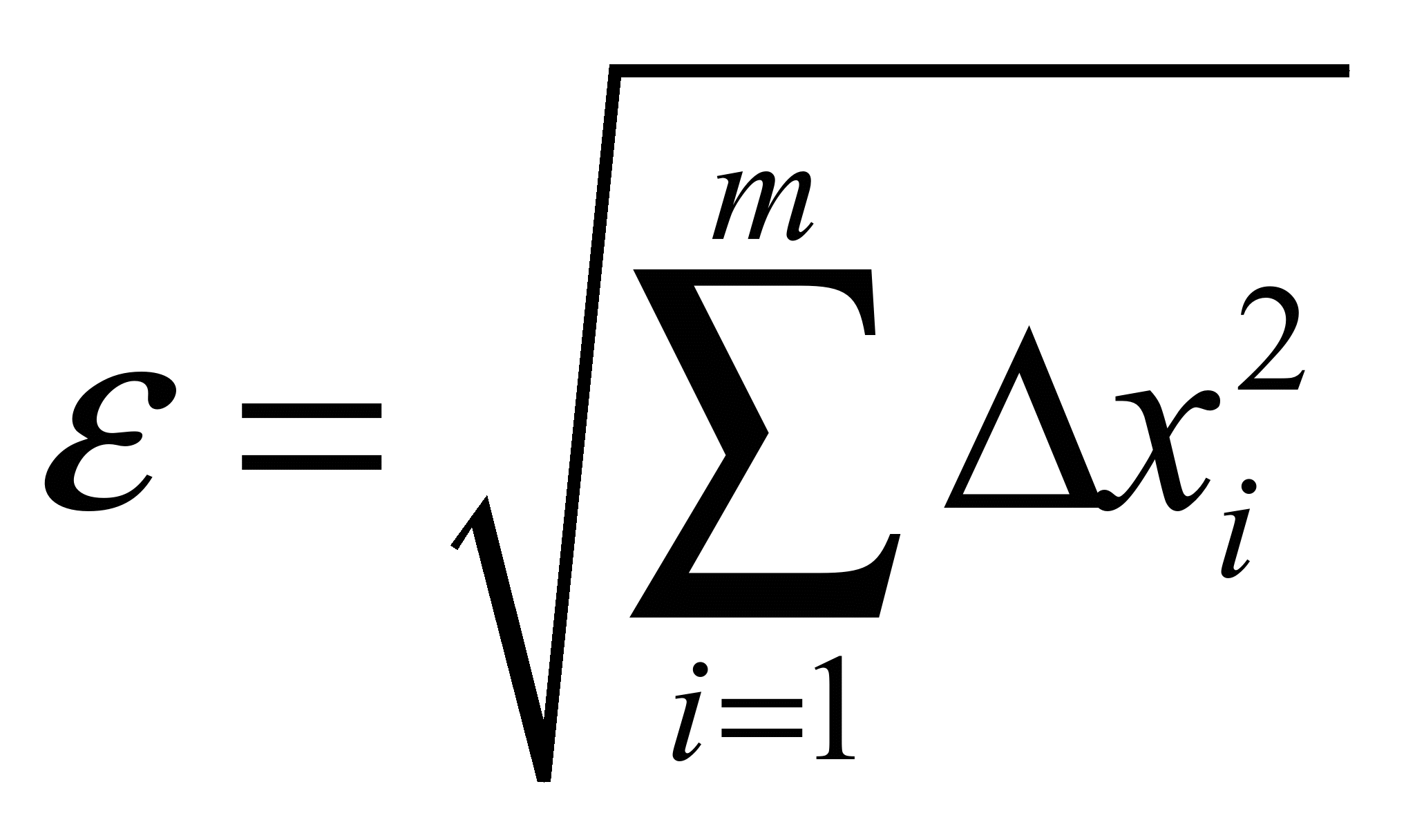 Приближенная оценка погрешности прямого однократного измерения. Для таких измерений в качестве результата принимают значение отсчета x, а оценивание погрешности производится на основе нормативных данных о свойствах используемых средств измерений. Поскольку эти данные относятся к множеству средств измерения данного типа, то у конкретного экземпляра прибора, используемого в измерении, действительные свойства могут значительно отличаться от нормированных (можно провести поверку). Тем не менее, не имея другой достоверной информации (либо не имея в ней нужды) о реальных метрологических характеристиках средства измерения, можно проводить оценку погрешности измерения на основе предельных норм, представляемых в технической документации на средства измерения. Такие оценки дают возможность оценить погрешность сверху, но для корректировки результата измерения или для введения поправок они недостаточно надежны. Общая схема следующая: Выбрав необходимое средство измерения (определяется исходя из условий измерительной задачи), уточнив условия измерения (нормальные или рабочие), оценивают возможные дополнительные погрешности прибора (если условия рабочие) и суммируют предел допускаемой основной погрешности и дополнительные погрешности 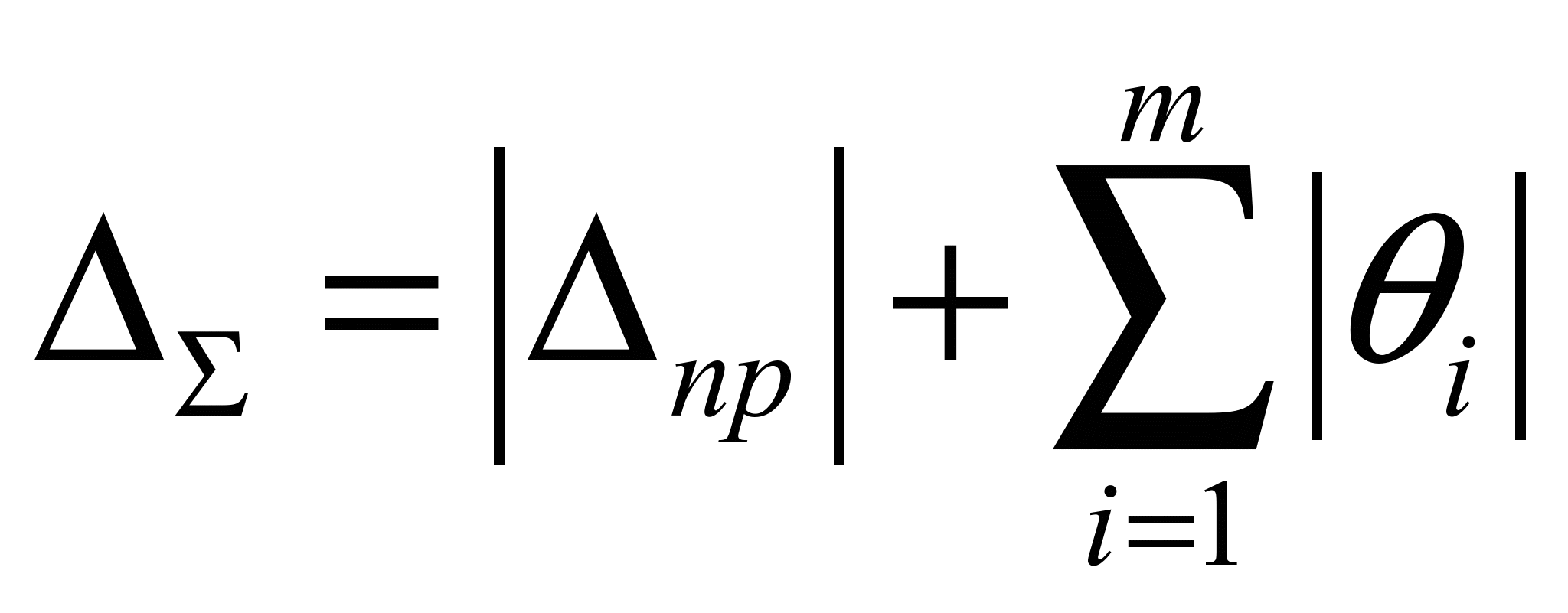 Таким образом находится верхняя оценка результата измерения. Методические погрешности должны быть учтены заранее, а личные (субъективные) при таких измерениях предполагаются малыми и не учитываются. Более точная оценка погрешности может быть получена статистическим сложением (а не простым) составляющих погрешности (например, вместо 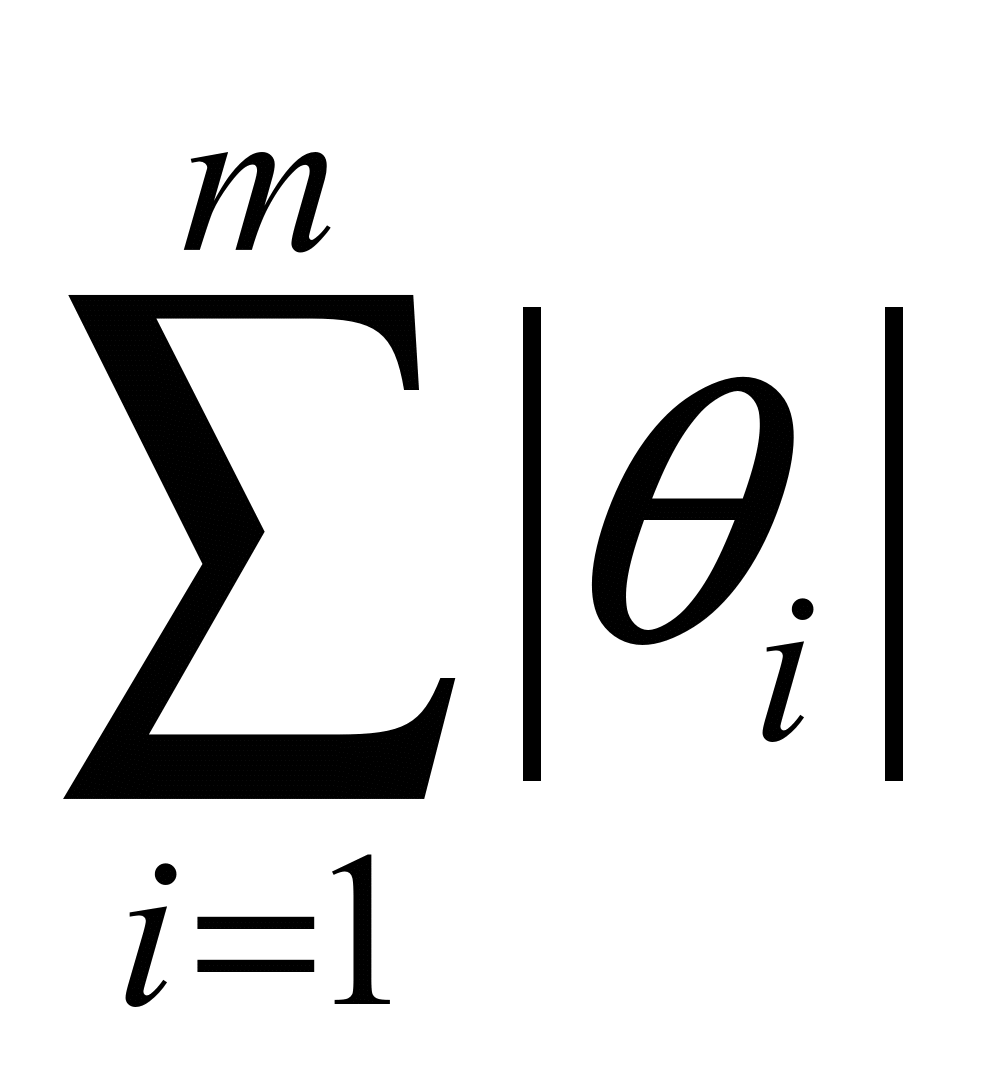 можно использовать можно использовать 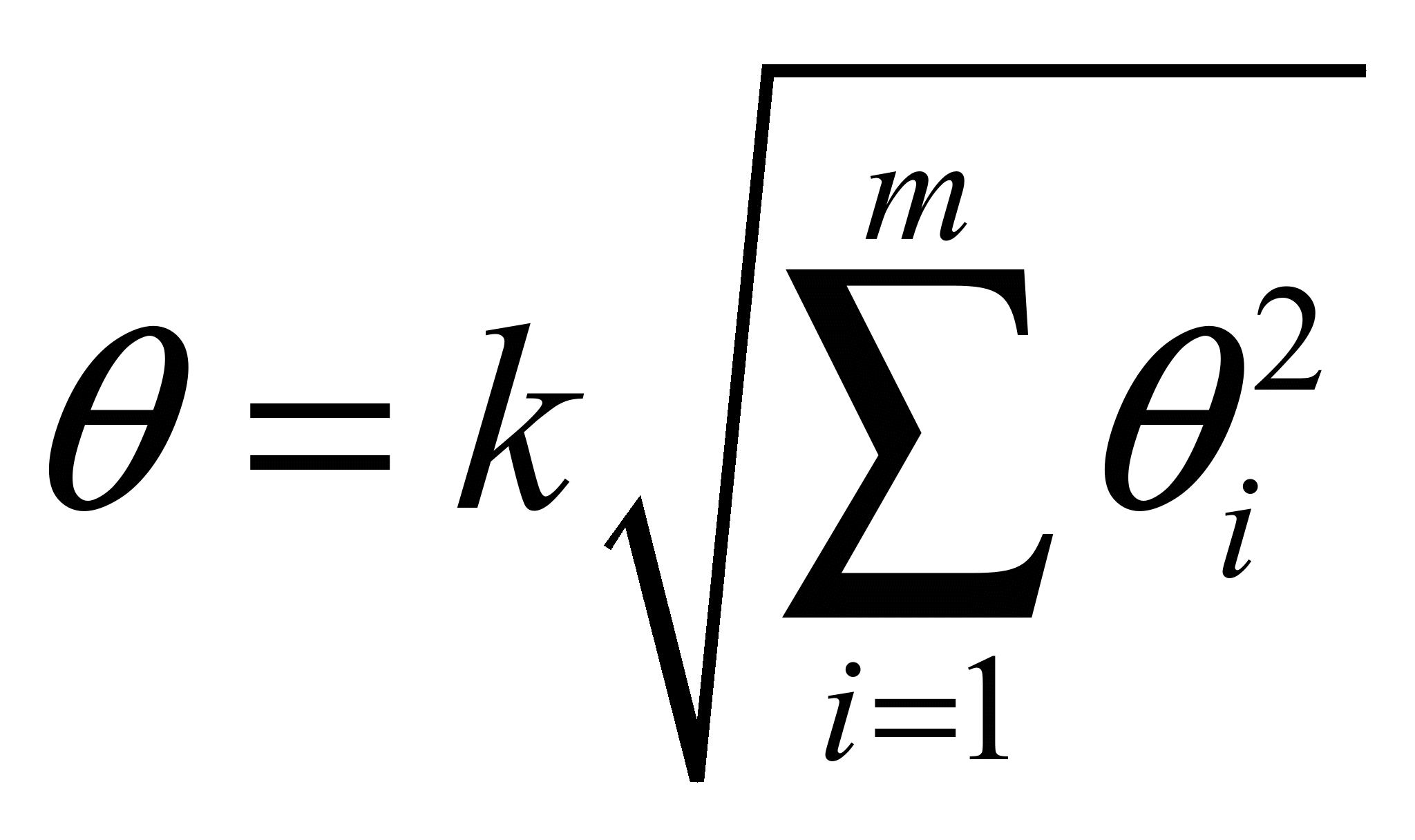 ) )Косвенные измерения При косвенных измерениях искомое значение величины находят расчетом на основе измерения других величин, связанных с измеряемой известной зависимостью: Поскольку каждое из Для оценки погрешностей существенно разделение косвенных измерений на линейные и нелинейные. При линейных косвенных измерениях уравнение измерений имеет вид: где Любые другие функции зависимости являются нелинейными. Погрешности результата могут быть заданы своими границами , либо доверительными границами с доверительными вероятностями . Если m<5 , то простая оценка погрешности результата Однако такая оценка является завышенной, так как такое суммирование означает, что погрешности измерения всех аргументов одновременно имеют максимальные значения и совпадают по знаку. Вероятность такого совпадения стремится к 0. Для определения более реалистичной оценки переходят к статистическому суммированию погрешностей аргументов, полагая, что в заданных границах погрешности аргументов распределены равномерно: 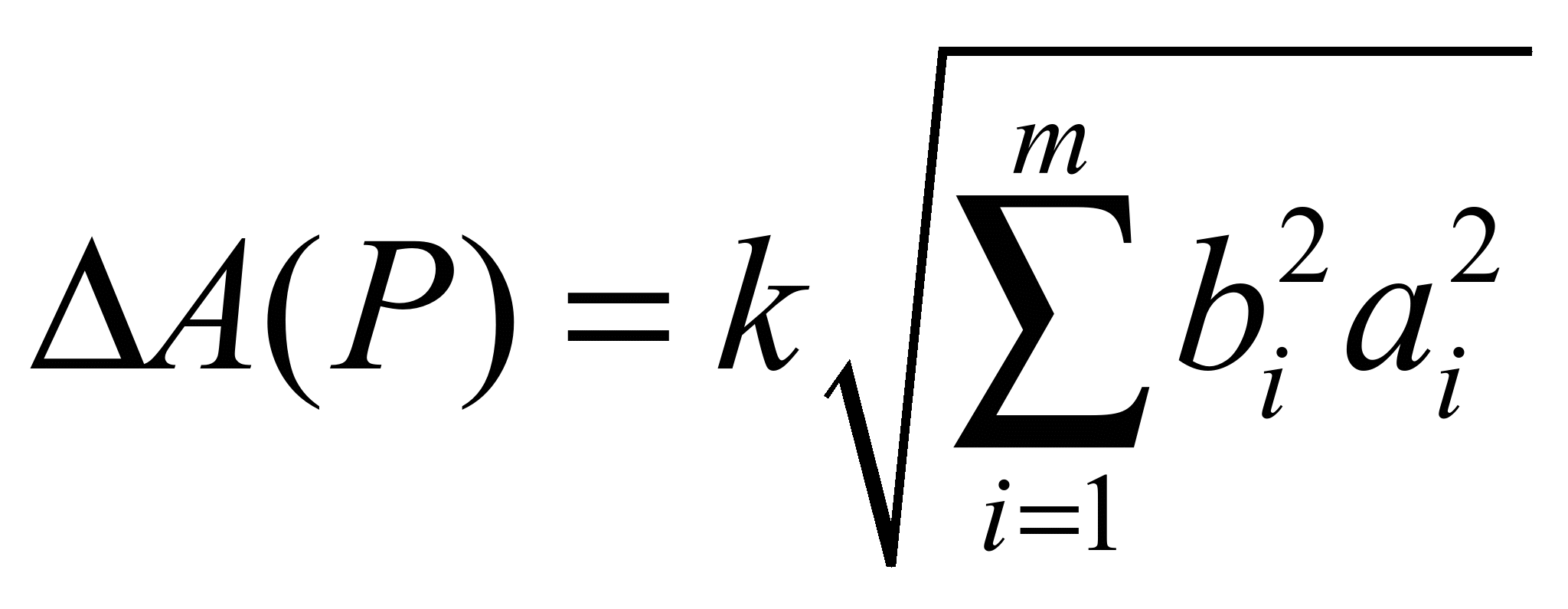 где где Нелинейные косвенные измерения характеризуется тем, что результаты измерения аргументов подвергаются функциональным преобразованиям. Как показано в теории вероятностей, любые, даже простейшие, функциональные преобразования случайной величины приводят к изменению законов их распределения. При сложной функции Для полного дифференциала функции A выражение запишем как: По определению полный дифференциал функции - это приращение функции, вызванное малыми приращениями ее аргументов. Полагая, что погрешности – это малые приращения, запишем: Полагая, что распределения погрешностей аргументов подчиняются равномерному закону, при числе слагаемых m<5 границы погрешности определяем А при m>5 по : 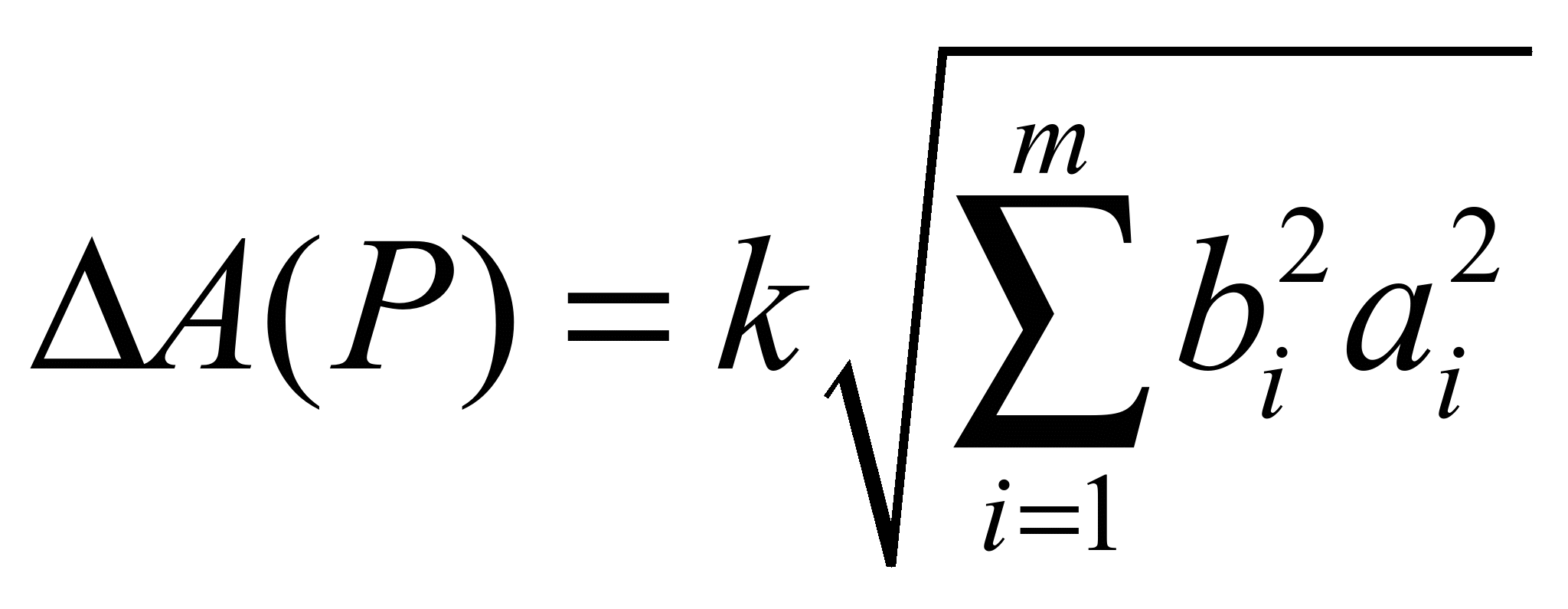 где 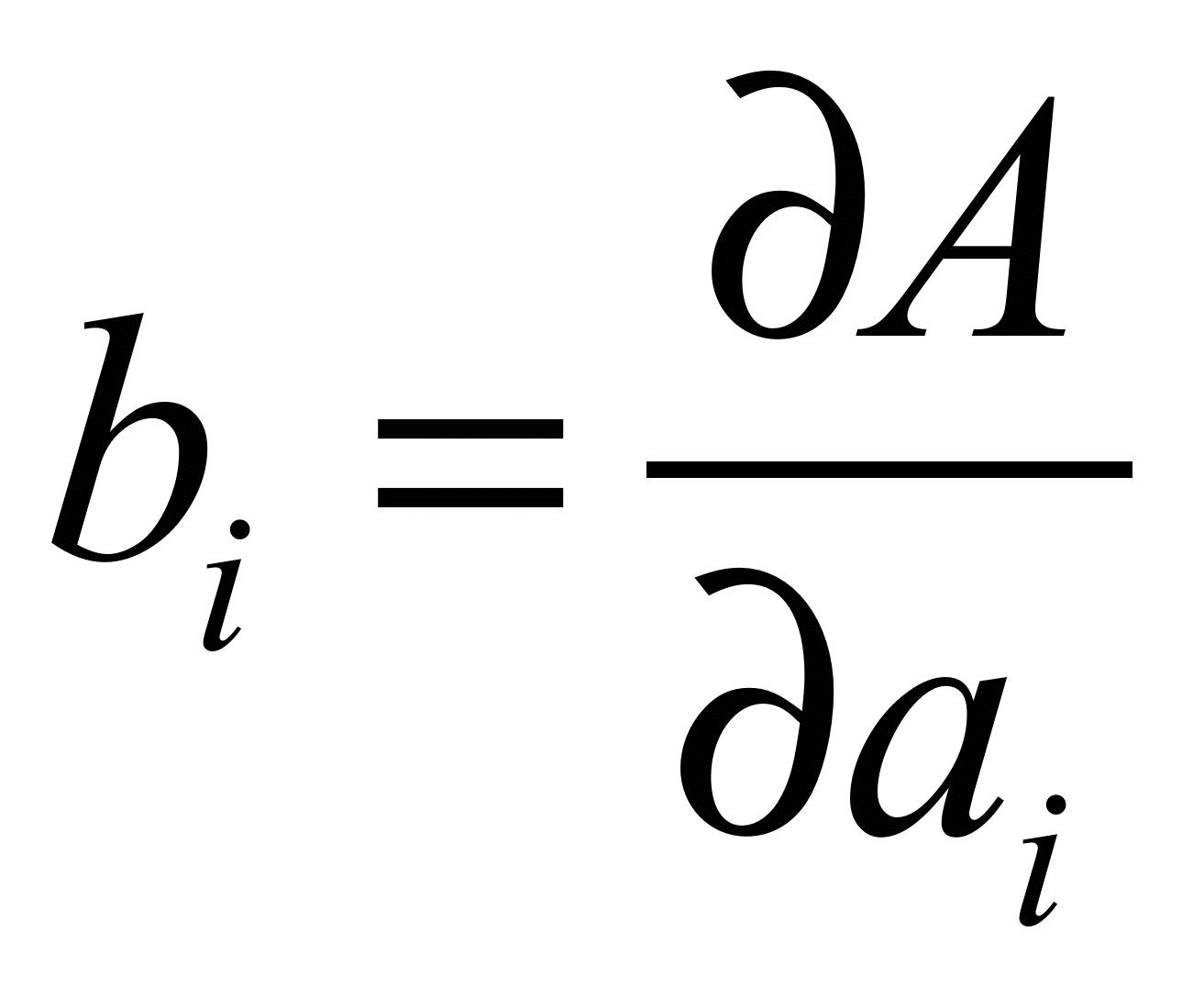 |
