вопросы по метре. Основные понятия метрологии. Классификация измерений и средств измерений. Принципы и методы измерений
 Скачать 0.74 Mb. Скачать 0.74 Mb.
|
|
по закономерности появления: 1) систематические погрешности Δс – составляющие погрешности, остающиеся постоянными или закономерно изменяющиеся при многократных измерениях одной и той же величины в одних и тех же условиях. 2) случайные погрешности – составляющие погрешности измерений, изменяющиеся случайным образом по значению и знаку при повторных измерениях одной и той же физической величины в одних и тех же условиях. Неизбежны, неустранимы, всегда имеют место в результате измерения.Их можно уменьшить многократными измерениями. 3) грубые погрешности (промахи) – погрешности, существенно превышающие ожидаемые при данных условиях измерения. При многократных наблюдениях промахи выявляют и исключают из рассмотрения в соответствии с определенными правилами. Т.о если исключить промахи, абсолютная погрешность измерения представляется как сумма случайной и систематич.погрешности. по виду источника погрешности: 1) методические – возникают из-за несовершенства метода измерений, упрощения объекта и модели измерения, из-за взаимного влияния средства измер-ия и объекта измерения; в процессе обработки измерения можно вычислить приблизительно; при переводе аналоговой вел-ны в числовую закладывается погрешность дискретизации. 2)инструментальные погрешности – возникают из-за несовершенства средств измерений, т.е. от их погрешностей (неточная градуировка, смещение нуля и пр.). 3)внешняя погрешность – связана с отклонением влияющих величин от нормальных значений (влияние влажности, температура, электромагнитных полей и пр.). Этот вид погрешности можно отнести к систематическим и дополнительным погрешностям средств измерения. 4)субъективная погрешность – вызвана ошибками оператора при отчете показаний. Устраняется применением цифровых средств измерений или автоматических методов измерения. по характеру поведения измеряемой величины в процессе измерений: 1) статические – возникают при измерении установившегося значения измеряемой величины 2) динамические – возникают при динамических измерениях. Причина – несоответствия временных характеристик прибора и скорости изменения измеряемой величины. по условиям эксплуатации средства измерения: 1) основная погрешность – имеет место при нормальных условиях эксплуатации, оговоренных в паспорте или технических условиях средств измерения 2) дополнительная погрешность – возникает из-за выхода какой-либо из влияющих величин за пределы нормальной области значений. Общая погрешность=систематическая+случайная Систематические погрешности В основу классификации системных погрешностей положена закономерность их поведения во времени. 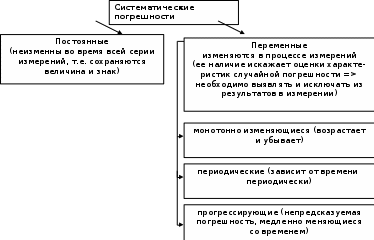 Отличительные особенности прогрессирующих (дрейфовых) погрешностей. их можно скорректировать поправками только в данный момент времени, далее они непредсказуемо меняются; изменение дрейфовых погрешностей во времени – нестационарный случайный процесс, который может быть описан весьма приблизительно в рамках теории стационарных случайных процессов. Причины: изменение температуры регулярные внешние помехи шкала градуировки старение прибора разрядка батареек Основные методы исключения систематических погрешностей: 1) Метод замещения – замена xизмер известной величиной А, получаемой с помощью регулируемой меры, чтобы показание прибора сохранялось неизменным. Погрешность неточного средства измерения устраняется, а абсолютная погр. определяется погрешностью отсчета измеряемой величины по указателю меры (или заменить на цифровой). 2) Метод компенсации погрешности по знаку – используется для устранения постоянной сиситематической погрешности. Выполняются два измерения: 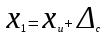 и и 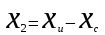 => =>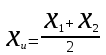 , где хи-измеряемая величины , где хи-измеряемая величины3) Метод противопоставления – применяется в радиоизмерениях для уменьшения постоянных систематических погрешностей при сравнении измеряемой величины с известной величной, воспроизводимой образцовой мерой. 4) Метод рандомизации – перевод систематических погрешностей в случайные: некоторая величина измеряется рядом однотипных приборов с последующей оценкой результата измерений в виде математического ожидания (средние арифметические значения) выполненного ряда наблюдений; т.е. от прибора к прибору метод погрешностей изменяется случайным образом. 5) Метод введения поправок – поправки определяются экспериментально или путем специальных теоретических исследований и задаются в виде формул, таблиц или графиков (например, этот метод хорош при устранении постоянных инструментальных погрешностей, которые можно выявить при поверке прибора). 6) Метод симметричных наблюдений – для выявления и исключения погрешностей, которые являются линейной функцией соответствующего аргумента (амплитуды, напряжения, времени, температуры и пр.). Используются для исключения погрешности, обусловленной, например, постепенным падением напряжения питания. 7) Графический метод – строится график, через точки проводят плавную линию, которая отражает тенденцию результата, если она есть. Если нет – переменную погрешность считают практически отсутствующей. При всех измерениях всегда остаются не исключенные остатки систематических погрешностей. 5. Метрологические характеристики средств измерения, их нормирование. Класс точности, интервальная оценка допускаемой погрешности. Метрологические характеристики средств измерений — это характеристики свойств, оказывающие влияние на результаты и погрешности измерений. - показывают точность прибора и позволяют оценить возможную погрешность прибора Техническое средство можно использовать для измерений только в том случае, если оно является средством измерений, т е. имеет нормированные метрологические характеристики. Основные метрологические характеристики оценивают пригодность средств измерений к измерениям в известном диапазоне с известной точностью и обеспечивают: сравнение средств измерений между собой и достижение их взаимозаменяемости; возможность установления точности измерений; выбор нужных средств измерений по точности и другим характеристикам; определение погрешностей измерительных систем и установок; оценку технического состояния средств измерений при их поверке. 1) Диапазон измерений — область значений измеряемой величины, для которой нормированы допускаемые погрешности измерительного прибора (средства измерения). 2) Диапазон показаний — размеченная область шкалы измерительного прибора, ограниченная ее начальным и конечным значениями, т. е. указанными на ней наименьшим и наибольшим возможными значениями измеряемой величины (он может быть шире диапазона измерений). 3) Предел измерений — наибольшее или наименьшее значение диапазона измерений. 4) Область рабочих частот (диапазон частот) — полоса частот, в пределах которой погрешность прибора, полученная при изменении частоты сигнала, не превышает допускаемого предела. 5) Градуировочная характеристик(цена деления) — зависимость, определяющая соотношение между сигналами на выходе и входе средства измерений в статическом режиме. 6) Чувствительность по измеряемому параметру — отношение изменения сигнала на выходе измерительного прибора к вызвавшему его изменению измеряемой величины S= дельта У/ Дельта Х где х — измеряемая величина; у — сигнал на выходе; 7) Предельная чувствительность— минимальная величина исследуемого сигнала, подаваемого на вход прибора, которая необходима для получения отсчета с погрешностью, не превосходящей допустимой. Наименьшее значение изменения физической величины, начиная с которого может осуществляться ее измерение, называется порогом чувствительности данного средства измерений. 8) Время измерения — время, которое требуется для определения значения измеряемой величины с заданной погрешностью. 9) Разрешающая способность (абсолютная) — минимальная разность двух значений измеряемых однородных величин, которая может быть различима с помощью прибора. 10) Быстродействие (скорость измерения) — максимальное число измерений в единицу времени, выполняемых с нормированной погрешностью. 11) Функция преобразования 12) Входной импеданс- это отношение изменения напряжения на входе к вызванному имизменению тока. К метрологическим характеристикам средств измерений относятся те, которые оказывают влияние на результаты и погрешности измерений. Среди них можно выделить несколько основных: градуировочные характеристики, определяющие зависимость входного сигнала от выходного; номинальное значение меры; пределы измерения; цена деления шкалы для аналоговых приборов; вид и параметры цифрового кода цифровых приборов. динамические характеристики, отражающие инерционные свойства средств измерений и необходимые для оценивания динамических погрешностей. инструментальные составляющие погрешности измерения. функции влияния, отражающие зависимость метролог. хар-ик ср-в измерений от воздействия влияющих величин или неинформативных параметров(напряжение, частота сети и т.д.) Метрологические хар-ки нормируются для нормальных условий применения средств измерений. Нормальными считаются такие условия, при которых изменением метролог.хар-ик под воздействием влияющих величин можно пренебречь. Инстурментальную погрешность в нормальной области значения влияющих величин называют основной. Выход значения влияющей величины за пределы нормальной области значений может привести к возникновению значительной составляющей инструментальной погрешности, называемой дополнительной. Классы точности средств измерений Определенная информация о возможной инструментальной составляющей погрешности измерения необходима, хотя бы для того, чтобы выбрать средство измерений, способное измерить размер с заданной точностью. Такая информация дается указанием класса точности средства измерений. Класс точности средства измерений– обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность. Другими словами класс точности дает возможность судить о том, в каких пределах находится погрешность средства измерений одного типа, но не является непосредственным показателем точности измерений данного средства измерения. Класс точности средства измерения устанавливают в стандартах, технических требованиях или в других нормативных документах.Для каждого класса точности определяют конкретные требования к метрологическимхарактеристикам, в совокупности определяющим уровень точности средства измерения данного класса. Пределы допускаемых погрешностей нормируют и выражают в форме абсолютной, относительной или приведенной погрешностей. Форма выражения зависит от характера изменения погрешностей. В общем случае абсолютная погрешность состоит из аддитивной (суммируемой с измеряемой величиной) и мультипликативной (умножаемой на измеряемую величину) составляющих. Интервальная оценка допускаемой погрешности Максимальная основная погрешность измерительного прибора, при которой он разрешен к применению, называется пределом допускаемой основной погрешности. 1) Пределы допускаемой абсолютной основной погрешности устанавливают по одной из формул:∆=±а или ∆=±(а+bx), гд х-значение измеряемой величины, a,b-положит-ые числа, не зависящие от х. Первая формула описывает аддитивную погрешность. Вторая формула –что в составе погрешности средства измерения присутствует сумма аддитивной и мультипликативной составляющих. При проведении измерений важное значение имеет диапазон измерений средства измерения. При уменьшении измеряемой величины х относительная погрешность средства измерения увеличивается и изменяется по гиперболе. Поэтому следует выбирать такой диапазон измерений, в котором значение х близко к Хк – большему по модулю из пределов измерений. 2) Пределы допускаемой приведенной основной погрешности устанавливаются по формуле: γ=∆/ХN * 100%=±p, где ХN– нормирующее значение, выраженное в тех же единицах, что и абсолютная погрешность, р – отвлеченное положит.число. Для средств измерений с равномерной, практически равномерной или степенной шкалой значение ХNпринимают равным: большему из пределов измерений или большему из модулей пределов измерений, если нулевое значение находится на краю или вне диапазона измерений сумме модулей пределов измерений, если нулевое значение наход-ся внутри диапазона измерений. 3) Пределы допускаемой относительной основной погрешности устанавливаются по формуле: δ=∆/х * 100%=±q, если ∆=±а q – отвлеченное положит. число. Пределы допускаемой дополнительной погрешности. 1) Предел допускаемой абсолютной дополнительной погрешности может указываться в виде: постоянного значения для всей рабочей области влияющей величины или постоянных значений по интервалам рабочей области влияющей величины отношения предела допускаемой доп.погрешности, соответс-его регламентированному интервалу влияющей величины, к этому интервалу. 6. Случайные погрешности и их описание. Законы распределения и их параметры. Аналитически случайные погрешности описывают и оценивают с помощью аппарата теории вероятностей и математической статистики. Рассмотрим некоторые числовые характеристики случайных величин. Математическое ожидание случайной величины – это сумма произведений всех ее возможных значений на их вероятности.математическое ожидание как дискретной так и непрерывной случайной величины есть неслучайная (постоянная) величина.Математическое ожидание приблизительно равно (тем точнее, чем больше число испытаний N) среднему арифметическому наблюдаемых значений случайной величины: 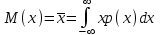 Х – обозначение случайной величины, xi– возможное значение Х. Для оценки рассеяния возможных значений(ширина разброса) случайной величины вокруг ее математического ожидания вводится понятие дисперсии – математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. 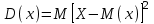 Средним квадратическим отклонением случайной величины x называется квадратный корень из дисперсии: 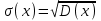 размерность среднего квадратического отклонения совпадает с размерностью самой случайной величины, поэтому в метрологии обычно используется 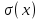 , а не D(x), которая имеет размерность квадрата случайной величины. , а не D(x), которая имеет размерность квадрата случайной величины.Для характеристики частоты появления различных значений случайной величины X (в нашем случае – погрешности прибора или результата измерения с учетом и ее систематической составляющей) теория вероятностей предполагает пользоваться указанием закона распределения вероятностей различных значений этой величины. Различают два вида законов 1) Интегральным законом или функцией распределения вероятностей F(x) случайной величины х называется функция, значение которой для любого х является вероятностью события, заключающегося в том, что случайная величина Х принимает значение, меньше х, т.е. 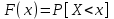 Это неубывающая функция х, изменяющаяся так, что F(-∞)=0, aF(+∞)=1. Она существует для всех случайных величин, как дискретных, так и непрерывных. Дискретная случайная величина – величина, которая принимает отдельные изолированные возможные значения с определенными вероятностями. Число возможных значений может быть как конечным, так и бесконечным. Непрерывная случайная величина – если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. 2) Для случайной величины с непрерывной и дифференцируемой F(x) можно найти дифференциальный закон распределения вероятностей, выражаемый как производная от F(x), т.е.p(x)=F’(x)Эта зависимость называется кривой плотности распределения вероятностей. Она всегда неотрицательна, т.е. p(x)≥0 и подчиняется условию нормировки: 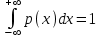 Примеры законов распределения: |
