Математика. К лекц.13.04 Конформные отображения. Основные понятия о конформных отображениях
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
Основные понятия |
| Окончательно получаем: | 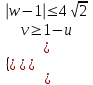 | или | 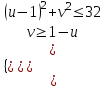 . . |

Функция f(z)=1/z
Определение
Инверсией в единичном круге называется такое преобразование, при котором каждой точке
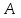 внутри (вне) круга ставится в соответствие точка
внутри (вне) круга ставится в соответствие точка 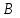 вне (внутри) круга, лежащая на луче, проведённом из центра круга в данную точку так, что произведение расстояний от этих точек до центра круга равно
вне (внутри) круга, лежащая на луче, проведённом из центра круга в данную точку так, что произведение расстояний от этих точек до центра круга равно 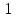 . То есть
. То есть 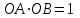 (рис. 27). Точки
(рис. 27). Точки 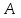 и
и 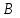 называются симметричными относительно единичной окружности.
называются симметричными относительно единичной окружности.Из этого определения следует, что точка, лежащая на окружности, симметрична самой себе, а точкой, симметричной центру окружности, является бесконечно удалённая точка.

Рассмотрим функцию
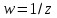 .
.Если построить окружность радиуса 1 с центром в точке
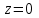 и рассмотреть точку, изображающую комплексное число
и рассмотреть точку, изображающую комплексное число 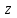 , то симметричная ей будет соответствовать числу
, то симметричная ей будет соответствовать числу 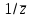 , так как
, так как 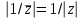 и
и 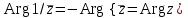 (последнее равенство показывает, что точки лежат на одном луче). Таким образом, отображение
(последнее равенство показывает, что точки лежат на одном луче). Таким образом, отображение 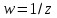 состоит из двух симметричных отражений: относительно единичной окружности (инверсия) и относительно действительной оси (рис. 28).
состоит из двух симметричных отражений: относительно единичной окружности (инверсия) и относительно действительной оси (рис. 28).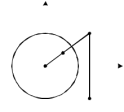
Производная
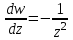 существует и отлична от нуля во всех точках плоскости, кроме
существует и отлична от нуля во всех точках плоскости, кроме 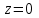 (
(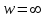 ) и
) и 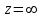 (
(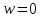 ). Таким образом, отображение
). Таким образом, отображение 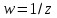 конформно во всех точках плоскости, кроме
конформно во всех точках плоскости, кроме 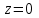 .
.Отображение
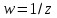 обладает круговым свойством: образом окружности является окружность, причём прямая считается окружностью, проходящей через бесконечно удалённую точку.
обладает круговым свойством: образом окружности является окружность, причём прямая считается окружностью, проходящей через бесконечно удалённую точку.Действительно, пусть
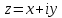 ,
, 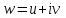 . Тогда отображение запишется так
. Тогда отображение запишется так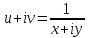
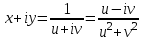 .
.Отсюда
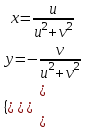 (4)
(4)Уравнение произвольной окружности в плоскости
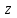 имеет вид
имеет вид 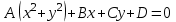 (при
(при 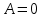 получается прямая, то есть окружность бесконечного радиуса). Подставим в него
получается прямая, то есть окружность бесконечного радиуса). Подставим в него 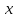 и
и 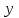 из (4)
из (4)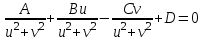 , или
, или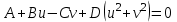 .
.Последнее уравнение — это уравнение окружности.
Видно, что образом окружности, не проходящей через точку
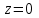 , является окружность, а образом окружности, проходящей через точку
, является окружность, а образом окружности, проходящей через точку 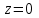 — прямая. При
— прямая. При 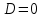 получаем уравнение прямой, то есть окружность, проходящая через начало координат в плоскости
получаем уравнение прямой, то есть окружность, проходящая через начало координат в плоскости 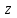 , переходит в прямую в плоскости
, переходит в прямую в плоскости 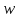 . Свойство доказано.
. Свойство доказано.Примеры
Найти образы линий и областей при преобразовании заданных линий и областей с помощью отображения
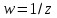 .
.1.
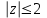 .
.Решение
Круг
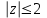 отобразится в область
отобразится в область 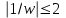 , то есть во внешность круга
, то есть во внешность круга 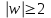 .
.2.
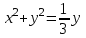 (рис. 29).
(рис. 29).Решение
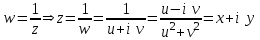
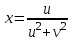 ,
, 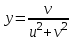
Подставим в уравнение исходной окружности и получим
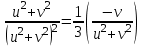 ,
, 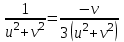 ,
, 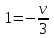
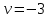
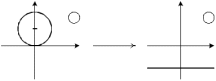
3.
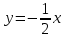
Решение
1 способ.
Поскольку прямая проходит через начало координат, инверсия переводит все точки прямой, находящиеся внутри единичного круга, на точки этой же прямой, лежащие вне единичного круга в той же четверти (рис. 30). Начало координат переходит в бесконечно удалённую точку, а обе точки на единичной окружности — сами в себя. Затем симметрия относительно действительной оси "разворачивает" прямую, сохраняя модуль угла наклона к действительной оси (рис. 30) (то есть угловой коэффициент только поменяет знак). Получаем прямую
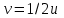 .
.2 способ. Формальное решение.
Рассуждая аналогично предыдущей задаче, получаем
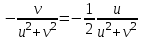
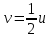 .
.
4.
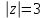
Решение
1 способ.
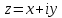 ,
, 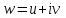
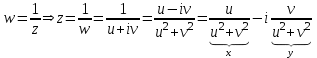
Теперь x и y выражены через u и v. Подставим эти соотношения в уравнение исходной окружности
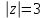 , то есть
, то есть 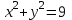
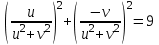 ,
, 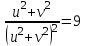 ,
, 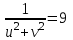 ,
,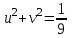 (рис. 31).
(рис. 31).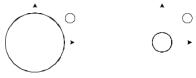
2 способ.
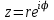 ,
, 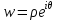
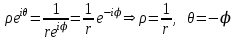
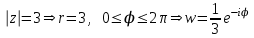 .
.Получили окружность радиуса
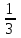 с центром в начале координат (если исходная окружность обходилась против часовой стрелки, то новая — по часовой стрелке).
с центром в начале координат (если исходная окружность обходилась против часовой стрелки, то новая — по часовой стрелке).3 способ.
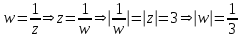 .
.
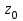 углы между линиями и величину растяжения линий, называется конформным в точке
углы между линиями и величину растяжения линий, называется конформным в точке 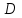 , если оно конформно в каждой точке этой области.
, если оно конформно в каждой точке этой области.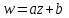 , где
, где 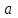 и
и 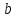 — комплексные постоянные,
— комплексные постоянные, 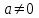 . Так как производная этой функции
. Так как производная этой функции 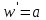 во всех точках плоскости существует и отлична от нуля, то линейное отображение конформно во всех точках плоскости.
во всех точках плоскости существует и отлична от нуля, то линейное отображение конформно во всех точках плоскости.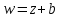

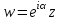 ,
, 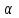 — действительное число.
— действительное число.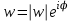 ,
, 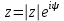 . Тогда
. Тогда 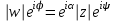 , то есть
, то есть 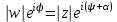 . В результате имеем соотношения для модуля и аргумента этих чисел
. В результате имеем соотношения для модуля и аргумента этих чисел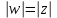 ,
, 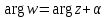 ,
,
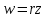 ,
, 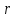 — действительное положительное число.
— действительное положительное число.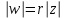 ,
, 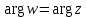 , то есть точка
, то есть точка 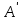 и
и 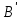 , то
, то 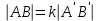 , где
, где 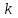 — постоянная величина, называемая коэффициентом подобия. Это преобразование иногда называют растяжением.
— постоянная величина, называемая коэффициентом подобия. Это преобразование иногда называют растяжением.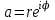 . Тогда
. Тогда 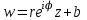 , и переход точки
, и переход точки 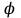 ;
;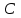 , соответствующих числам
, соответствующих числам 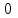 ,
, 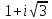 ,
, 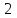 , лежащий в плоскости
, лежащий в плоскости 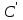 плоскости
плоскости 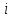 ,
, 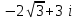 ,
, 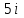 (рис. 25).
(рис. 25).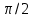 :
: 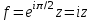 ;
;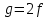 ;
;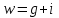 .
.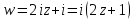 .
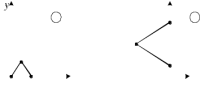
.
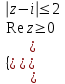 при отображении
при отображении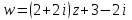 .
.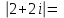
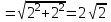 . Образом полукруга будет полукруг с центром
. Образом полукруга будет полукруг с центром 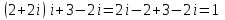 и радиусом
и радиусом 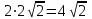 . Угол поворота
. Угол поворота 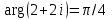 , то есть образ границы круга (прямой
, то есть образ границы круга (прямой 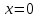 ) — прямая с угловым коэффициентом, равным
) — прямая с угловым коэффициентом, равным 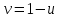 (рис. 26).
(рис. 26).