лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4

• Название: Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
• Анкор: лекции по дм
• Дата: 08.02.2021
• Размер: 1.51 Mb.
• Имя файла: лекции.docx
• Тип: Документы; #174835
• страница: 20 из 40

Операции над графами:

Объединение графов.

Пусть G₁(X₁,E₁) и G₂(X₂,E₂) – произвольные графы.

Определение 11.3. Объединением G₁G₂графов G₁ и G₂ называется граф с множеством вершин X₁X₂, и с множеством ребер (дуг) E₁E_2.

Рассмотрим операцию на примере графов G₁(X₁,E₁) и G₂(X₂,E₂), приведенных на рис. 11.1. Множества вершин первого и второго графов соответственно равны X₁ = {x₁, x₂, x₃} и X₂ = {x₂, x₃, x₄}, а множество вершин результирующего графа определится как X = X₁X₂ = {x₁, x₂, x₃, x₄}. Аналогично определяем множества дуг графа:

E₁ = {(x₁, x₂), (x₁, x₃), (x₂, x₁), (x₃, x₃)}. E₂ = {(x₂, x₄), (x₃, x₂)_, (x₄, x₂)}.

E = {(x₁, x₂), (x₁, x₃), (x₂, x₁), (x₃, x₃), (x₂, x₄), (x₃, x₂)_, (x₄, x₂)}.

Результирующий граф G(X,E) = G₁(X₁,E₁)G₂(X₂,E₂) также приведен на рис. 11.1.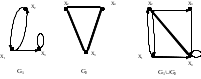



Рисунок 11.1

Операция объединения обладает следующими свойствами, которые следуют из определения операции и свойств операций на множествах:

1. 
   G₁G₂ = G₂G₁ – свойство коммутативности;
   
2. 
   G₁(G₂G₃) = (G₁G₂)G₃ – свойство ассоциативности.
   

Операция объединения графов может быть выполнена в матричной форме. Для графов с одним и тем же множеством вершин справедлива следующая теорема.

Теорема 11.2. Пусть G₁ и G₂ – два графа (ориентированные или не ориентированные одновременно) с одним и тем же множеством вершин X, и пусть A₁ и A₂ – матрицы смежности вершин этих графов. Тогда матрицей смежности вершин графа G₁G₂ является матрица A = A₁A₂, образованная поэлементным логическим сложением матриц A₁ и A₂.

Рассмотрим выполнение операции объединения графов, множества вершин которых не совпадают. Пусть G₁(X₁,E₁) и G₂(X₂,E₂) – графы без параллельных ребер и множества X₁ и X₂ вершин этих графов не совпадают. Пусть A₁ и A₂ – матрицы смежности их вершин графов. Для таких графов операция объединения может быть выполнена следующим образом.

В соответствии с определением операции объединения графов найдем множество вершин результирующего графа как X₁X₂. Построим вспомогательные графы G’₁ и G’₂, множества вершин которых есть множество X₁X₂, а множество ребер (дуг) определяется множествами E₁ для графа G^’₁ и E₂ для графа G^’₂. Очевидно, что матрицы A’₁ и A’₂ смежности вершин этих графов могут быть получены из матриц A₁ и A₂ путем добавления в них дополнительных столбцов и строк с нулевыми элементами.

Применив к графам G’₁ и G’₂ теорему 4.1, найдем матрицу смежности вершин графа G’₁G’₂ как A’₁A’₂. Очевидно, что полученной матрице смежности вершин соответствует граф, множество вершин которого равно X₁X₂, а множество ребер определяется, как E₁E₂, что соответствует операции объединения графов.

Пример. Выполнить в матричной форме операцию объединения графов G₁ и G₂, представленных на рис. 1.

Составим матрицы смежности вершин графов.

			x1	x2	x3				x2	x3	x4
		x1	0	1	1			x2	0	0	1
A1	=	x2	1	0	0	A2	=	x3	1	0	0
		x3	0	0	1			x4	0	1	0

Множество вершин результирующего графа X₁X₂ = {x₁, x₂, x₃, x₄}. Составим матрицы смежности вершин вспомогательных графов G’₁ и G’₂.

			x1	x2	x3	x4				x1	x2	x3	x4
		x1	0	1	1	0			x1	0	0	0	0
A’1	=	x2	1	0	0	0	A’2	=	x2	0	0	0	1
		x3	0	0	1	0			x3	0	1	0	0
		x4	0	0	0	0			x4	0	0	1	0

Матрица A = A’₁A’₂ имеет вид

			X1	x2	x3	x4
		x1	0	1	1	0
		x2	1	0	0	1
A = A’1A’2	=	x3	0	1	1	0
		x4	0	0	1	0

Полученная матрица смежности вершин A’₁ A’₂ соответствует графу G₁G₂, изображенному на рис.11.1.