лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Основные понятия теории множеств. Способы задания множествОпределение 1.1. Множество – это любая, определенная совокупность объектов. Объекты из которых составлено множество называют его элементами. Элементы множества различны и отличны друг от друга. Множества обозначают прописными буквами латинского алфавита, а их элементы – строчными. Например N, Z, Q, R – множества натуральных, целых, рациональных и действительных чисел. N={1, 2, 3…} A={a1, a2, a3…} Если объект х является элементом множества М, то говорят, что хМ. Если х не является элементом множества М, то говорят, что хМ. Одно множество равно другому, если выполняется условие: A=B | A 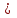 B & B B & B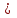 A AМножество не содержащее элементов называется пустым. Его обозначают Ø. Обычно, в конкретных обсуждениях, элементы всех множеств берутся из некоторого одного достаточно широкого множества U (своего для каждого множества), которое называется универсальным множеством или универсумом. В общем случае множества могут быть конечными и бесконечными. Конечное множество – это такое множество, для которого существует натуральное число, равное количеству элементов множества, и называемое мощностью множества и обозначаемое |A|. Чтобы задать множество нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами: 1) перечислением элементов множества А={a1, a2,…, an|n=6} (перечислением можно задавать только конечное множество); 2) характеристическим предикатом M={ x | P(x) }, где P(x) – предикат. Характеристический предикат – это некоторое условие, выраженное в форме логического утверждения, возвращаемое логическое значение. Если для данного элемента условие выполнено, т.е. P(x) = 1, то этот элемент принадлежит определяемому множеству, в противном случае – не принадлежит. Пример 1.1.: M = { x | xN & x < 10} P(x) = (11) = ( 11 & 11 < 10 ) = 0  11М 11М3) порождающей процедурой: M={ x | x := f } Порождающая процедура – это процедура, которая будучи запущенной порождает некоторые объекты, являющиеся элементами порождаемого множества. Иначе говоря, порождающая процедура – последовательность действий, которые формируют некоторые объекты по заданному правилу. Пример 1.2.: M = { x | x := from 1 to 9 generate x} Диаграммы Венна.Определение 1.2. Диаграммы Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматривать как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств. Операции над множествами.Самого понятия множество недостаточно, следует определить способы конструирования новых множеств из уже имеющихся, т.е. задать операции над множествами. Множество A содержится в множестве B (множество B включает множество A), если элемент множества A есть элемент множества B. A 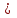 B:=xA=>xB. В этом случае A называют подмножеством B, а B – надмножеством A. Также возможен случай когда множество А включено в В и может полностью совпадать с ним (А B:=xA=>xB. В этом случае A называют подмножеством B, а B – надмножеством A. Также возможен случай когда множество А включено в В и может полностью совпадать с ним (А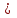 В). В).Обычно рассматривают следующие операции над множествами: Объединение AB := { x | xA 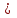 xB} xB} Пересечение AB:= { x | xA & xB}  Разность A \ B := { x | xA 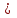 xB} xB} Симметричная разность AB:=(AB) \ (AB)  5. Дополнение :={ x | x A }Операция Дополнение подразумевает некоторый универсум U: := U \ A  |
