лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Тема 4. Замыкание отношений. Транзитивное замыкание, рефлексивное замыкание. Алгоритм Уоршалла вычисления транзитивного замыкания.Замыкание отношений.Замыканием отношения R относительно свойства P называется такое множество R*, что: 1. RR*. 2. R* обладает свойством P. 3. R* является подмножеством любого другого отношения, содержащего R и обладающего свойством P. Замыкание является весьма общим математическим понятием. Неформально говоря, замкнутость означает, что многократное выполнение допустимых шагов не выводит за определенные границы. Пример Пусть на множестве A={1,2,3,4} задано отношение R={(1,2),(3,4),(4,2)}. Видно, что отношение R не симметрично, не рефлексивно и не транзитивно. Замыканием R относительно свойства симметричности является R*={(1,2),(3,4),(4,2);(2,1),(4,3),(2,4)}. Замыканием R относительно рефлексивности является R*={(1,2),(3,4),(4,2);(1,1),(2,2),(3,3),(4,4)}. Замыканием R относительно транзитивности является множество R*={(1,2),(3,4),(4,2);(3,2)}. Транзитивное замыкание отношенийОпределение 4.1. Отношение 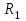 называется транзитивным замыканием отношения называется транзитивным замыканием отношения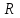 , определенного на множестве M, тогда и только тогда, когда существуют такие , определенного на множестве M, тогда и только тогда, когда существуют такие 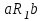 , что , что 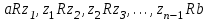 . . Пример На множестве N определено отношение 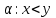 . Тогда транзитивное замыкание этого отношения для значений 1<2<…<6 будет отношение 1<6. (Рисунок 4.1) . Тогда транзитивное замыкание этого отношения для значений 1<2<…<6 будет отношение 1<6. (Рисунок 4.1) Рисунок 4.1 Транзитивным замыканием отношения «быть сыном» является отношение «быть прямым потомком». Транзитивным замыканием отношения «иметь общую стену» для жильцов одного дома является отношение « жить на одном этаже». Пример. Пусть R задано на M, 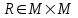 . Rтранзитивно, если для любых a,b,с из аRbи bRс следует аRс. Вматрице такого отношения должно выполняться следующее условие: если в i-й строке стоит единица, например в j-й координате (столбце) строки, т.е. . Rтранзитивно, если для любых a,b,с из аRbи bRс следует аRс. Вматрице такого отношения должно выполняться следующее условие: если в i-й строке стоит единица, например в j-й координате (столбце) строки, т.е. 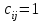 , то всем единицам в j-й строке (пусть этим единицам соответствуют k-е координаты такие, что , то всем единицам в j-й строке (пусть этим единицам соответствуют k-е координаты такие, что 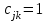 ) должны соответствовать единицы в i-й строке в тех же k-хкоординатах, т.е. ) должны соответствовать единицы в i-й строке в тех же k-хкоординатах, т.е. 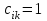 (и, может быть, еще и в других координатах). Это условие иллюстрируется на рисунке 4.2, где кружком выделена единица (и, может быть, еще и в других координатах). Это условие иллюстрируется на рисунке 4.2, где кружком выделена единица 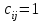 , для которой производится проверка условия, а стрелками показана последовательность проверки данного условия. , для которой производится проверка условия, а стрелками показана последовательность проверки данного условия.В матрице транзитивного отношения это условие должно выполняться для любых  таких, что таких, что 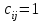 . И наоборот, если в матрице Rимеется хотя бы одна единица . И наоборот, если в матрице Rимеется хотя бы одна единица 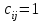 , для которой данное условие не выполняется, то Rне транзитивно. , для которой данное условие не выполняется, то Rне транзитивно.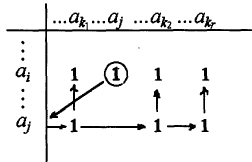 Рисунок 4.2 |
