лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Способы задания операций.Так как операция является функцией, то для ее задания применимы любые способы задания функций, перечисленные в предыдущем параграфе. Приведем некоторые наиболее употребляемые способы представления унарных и бинарных операций. 1. Способы задания унарных операций φ: М → М на конечном множестве М = {  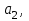 … , … ,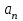 } }• Перечнем всех аргументов а из М (для частично определенной операции - из ее области определения 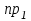 φ φ 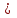 М) и соответствующих им значений b, a, b М) и соответствующих им значений b, a, b 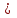 M, представленных строкой M, представленных строкойφ = ( 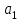 → → 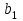 , ,  → →  , ... , , ... , 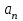 → → 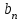 ), ),а чаще парой строк: φ = 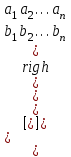 . .В случае, если предварительно зафиксирован список (последовательность) элементов (а 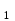 ,а ,а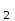 ,...,а ,...,а ) множества М, то для задания операции φ достаточно указать вектор значений (b ) множества М, то для задания операции φ достаточно указать вектор значений (b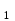 , b , b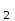 ,..., b ,..., b ). При этом φ(а ). При этом φ(а ) = b ) = b , т.е. результат выполнения операции φ для i-го аргумента списка равен i-й компоненте вектора значений. , т.е. результат выполнения операции φ для i-го аргумента списка равен i-й компоненте вектора значений.• Списком всех пар "аргумент-значение" (а, b) 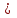 φ, а, b φ, а, b 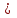 М, для всех возможных значений аргументов: М, для всех возможных значений аргументов:φ ={( 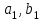 ),( ),(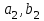 ),...,( ),...,( )}. )}.Число таких пар |пр 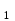 φ | = m φ | = m   М М = n. = n.• Формулой φ(а) = b, например lg а = b. 2. Способы задания бинарных операций φ : М × М 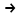 М на конечном множестве М= { М на конечном множестве М= { }: }:Таблица Кэли• Таблицей Кэли - для чего слева и сверху таблицы выписываются все значения аргументов а и b из множества М соответственно, а на пересечении строки, соответствующей аргументу а, и столбца, соответствующего аргументу b, записывается результат с операции φ над а и b. На рис. 5.2. приведена таблица Кэли для операции, называемой "сложением по модулю 3" на множестве М = {0, 1, 2} и обозначаемой "mod 3", или 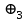 (результат с выполнения операции (результат с выполнения операции 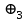 равен остатку от деления суммы аргументов (а + b) на З ). равен остатку от деления суммы аргументов (а + b) на З ).
Рис. 5.2. Списком всех троек (а, b, с), где а,b - соответственно первый и второй аргументы из М, с-результат выполнения операции φ над а и b, a,b,c 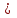 M. Для всюду определенной операции число всех троек в списке M. Для всюду определенной операции число всех троек в списке |M×M|= 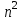 . Например, для операции сложения по модулю 3: . Например, для операции сложения по модулю 3: 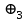 ={(0,0,0), (0,1,1), (0,2,2), (1,0,1), (1,1,2), (1,2,0), (2,0,2), (2,1,0), (2,2,1)}. ={(0,0,0), (0,1,1), (0,2,2), (1,0,1), (1,1,2), (1,2,0), (2,0,2), (2,1,0), (2,2,1)}.• Формулой φ (а, b) = с - так называемое префиксное представление операции; иное - инфиксное - представление бинарной операции формулой a φ b = c, например, а 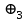 b = с, где b = с, где 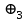 - операция сложения по модулю 3. - операция сложения по модулю 3. |
