лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
) и B = (М2;>) гомоморфны, но не изоморфны.
'Петрова' и Г( 'Иванов") = 37, Г( 'Петров') = 26, то и 37 > 26.
) и B=(М2;>)?Тема 6. Алгебраическая система. Гомоморфизмы. Проверка условия гомоморфизма. Изоморфизмы. Изоморфные алгебры. Изоморфизм модели. Примеры изоморфных алгебр.Алгебраическая системаОпределение 6.1. Множество Μ вместе с заданными на нем операциями {φ1, φ2,...,φ n} называется алгеброй. Обозначение алгебры: 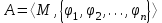 , где М называется основным множеством (несущим множеством, носителем), а , где М называется основным множеством (несущим множеством, носителем), а 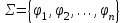 - сигнатурой алгебры A. - сигнатурой алгебры A.Примером алгебры является полугруппа - множество Μ с заданной на нем одной бинарной ассоциативной операцией (обозначается: · ), т.е. A= {М; ·}, например множество натуральных чисел N с операцией сложения + на нем, т.е. A= {Ν; +} является полугруппой. Типом алгебры A называется вектор парностей операций сигнатуры. Например, в алгебре A= {R; +, χ}, где R - множество действительных чисел, + и χ - соответственно операции сложения и умножения (такая алгебра называется полем действительных чисел), сигнатура Σ = {+, χ} включает две бинарные операции - сложение и умножение. Поэтому тип данной алгебры (2,2). Определение 6.2. Алгебраическую систему 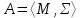 , где множество , где множество  состоит из одной двухместной операции, называется группоидом. состоит из одной двухместной операции, называется группоидом.Определение 6.2. кольцом называется алгебра с двумя операциями 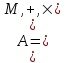 , если обладает следующими свойствами: , если обладает следующими свойствами: - Авелева группа - Авелева группа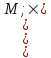 - полугруппа - полугруппаОперация умножения дистрибутивна относительно сложения ( 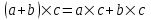 ). ).Определение 6.3. Множество Μ вместе с заданными на нем отношениями {R1 R2, ..., Rn} называется моделью. Обозначение модели: 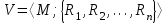 , где М - несущее множество (универсум), , где М - несущее множество (универсум), 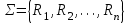 – сигнатура модели V. Например, моделью V1| является множество М1, чисел с отношениями: "быть больше" (>) и "быть равным" (=), т.е. V1 = (M1; >, =), или некоторое множество Mг людей с отношением R - "быть руководителем", т.е. Vг = (М2; R), и т.д. – сигнатура модели V. Например, моделью V1| является множество М1, чисел с отношениями: "быть больше" (>) и "быть равным" (=), т.е. V1 = (M1; >, =), или некоторое множество Mг людей с отношением R - "быть руководителем", т.е. Vг = (М2; R), и т.д.Определение 6.4. Множество Μ вместе с заданными на нем операциями {φ1, φ2, ..., n} и отношениями {R1, R2, ···,Rn} называется алгебраической системой, или алгебраической структурой. Обозначение алгебраической структуры: V= (Μ; φ1, φ2,..., φn; R1, R2,..., Rn). Если полугруппа обладает коммутативным свойством ( 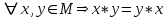 ), то её называют Авелевой группой. ), то её называют Авелевой группой.Примером алгебраической структуры является так называемая решетка - множество Μ с заданными на нем: одним бинарным отношением частичного порядка (обозначение ≤) и двумя бинарными операциями ( ∩ и U ): {М;≤; ∩, U }. Таким образом, алгебры - это алгебраические структуры с пустым множеством отношений. Другим частным случаем алгебраических структур являются модели, т.е. множества, на которых заданы только отношения. Гомоморфизмы. Проверка условия гомоморфизма. Изоморфизмы. Изоморфные алгебры. Изоморфизм модели. Примеры изоморфных алгебр.Пусть между множествами А и В установлено соответствие Г - отображение А вB, т.е.  . Это означает, что каждому элементу а из А поставлен в соответствие Г единственный элемент α из В, т.е. Г(а) = α. Пусть также на множестве А задана операция φ, на множестве В - операция ψ, обе одинаковой арности, например обе бинарные, так что . Это означает, что каждому элементу а из А поставлен в соответствие Г единственный элемент α из В, т.е. Г(а) = α. Пусть также на множестве А задана операция φ, на множестве В - операция ψ, обе одинаковой арности, например обе бинарные, так что  , где а,b,с €А, и , где а,b,с €А, и 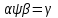 , где α,β,γ€В. Таким образом, имеем две алгебры <Α;φ> и <B;ψ>. , где α,β,γ€В. Таким образом, имеем две алгебры <Α;φ> и <B;ψ>.Определение 6. 5. Тогда отображение  называется гомоморфизмом алгебры <Α;φ> в алгебру <B;ψ>, если выполняется условие: называется гомоморфизмом алгебры <Α;φ> в алгебру <B;ψ>, если выполняется условие: 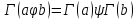 . (Рисунок 6.1) . (Рисунок 6.1) Рисунок 6.1. Условие гомоморфизма 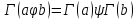 требует (см. рис. 6,1), чтобы отображение Г результата с=аφb выполнения на множестве А операции φ над элементами α и b, т.е. Г(с)=Г(aφb), совпадало с результатом γ выполнения на множестве В операции ψ над отображениями этих элементов, т.е. над Γ(α)=α и Γ(b)=β. требует (см. рис. 6,1), чтобы отображение Г результата с=аφb выполнения на множестве А операции φ над элементами α и b, т.е. Г(с)=Г(aφb), совпадало с результатом γ выполнения на множестве В операции ψ над отображениями этих элементов, т.е. над Γ(α)=α и Γ(b)=β. Проверка уcловия гомоморфизма заключается в следующем. В соответствии с левой частью сначала над элементами а и b из А должна быть выполнена операция φ, а затем результат с=αφb выполнения операции φ отображается из А в множество В. В соответствии с правой частью условия Γ(α)=α и Γ(b)=β требуется сначала выполнить отображения элементов α и b из множества А в В, т.е. найти Г(а)=а и Г(b)=β, а затем над α и β выполнить операцию ψ (заданную на множестве В), т.е. Γ(α) ψ Г(&), или α ψ β = γ. Условие 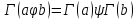 будет выполнено, если результат отображения элемента с=αφb из А в В совпадает с элементом γ из В, т.е. если Г(с)=у. будет выполнено, если результат отображения элемента с=αφb из А в В совпадает с элементом γ из В, т.е. если Г(с)=у.Определение 6. 6. Если при этом отображение  является взаимно однозначным соответствием, оно называется изоморфизмом алгебры <Α;φ> на алгебру <B;ψ>. В этом случае существует и обратное отображение является взаимно однозначным соответствием, оно называется изоморфизмом алгебры <Α;φ> на алгебру <B;ψ>. В этом случае существует и обратное отображение 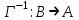 , также взаимно однозначно: , также взаимно однозначно: 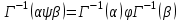 . .Определение 6. 7. Отображение Г-1 - это, в свою очередь, изоморфизм В на А. Итак, если существует изоморфизм А на В, то существует изоморфизм В на А. При этом алгебры <Α;φ> и <B;ψ> называются изоморфными. В более общем случае, если на множествах А и В заданы несколько операций соответственно <Α; {φ1 φ2,..., φn}> и <В; {ψ1, ψ2.....ψn}>, отображение  является гомоморфизмом алгебры <Α; {φ1 φ2,..., φn}> в алгебру <В; {ψ1, ψ2.....ψn}>, если условия, аналогичные является гомоморфизмом алгебры <Α; {φ1 φ2,..., φn}> в алгебру <В; {ψ1, ψ2.....ψn}>, если условия, аналогичные 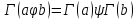 , выполняются для каждой пары операций φ1 и ψ1 ... ,φn и φn. , выполняются для каждой пары операций φ1 и ψ1 ... ,φn и φn.В силу взаимной однозначности соответствия  при изоморфизме мощности основных множеств изоморфных алгебр равны. Поэтому проверка алгебр на изоморфизм сводится к проверке условия гомоморфизма для каждой пары операций и установления взаимной однозначности соответствия Г (равной мощности множеств А и В). при изоморфизме мощности основных множеств изоморфных алгебр равны. Поэтому проверка алгебр на изоморфизм сводится к проверке условия гомоморфизма для каждой пары операций и установления взаимной однозначности соответствия Г (равной мощности множеств А и В).Аналогично определяется гомоморфизм (изоморфизм) множеств с отношениями - моделей 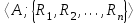 и и 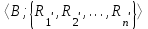 . .Пусть, например, на множестве А задано бинарное отношение R(а,b) а,b € А, и на множестве В—бинарное отношение R'(α,β), α,β € В. Тогда отображение  является гомоморфизмом модели является гомоморфизмом модели 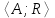 в модель в модель  , если для любой пары элементов а,b из А такой, что а и b находятся в отношении R, следует, что их отображения Г(а)=α и Г(b)=β находятся в отношении R' (см. рис. 6.2.), т.е. , если для любой пары элементов а,b из А такой, что а и b находятся в отношении R, следует, что их отображения Г(а)=α и Г(b)=β находятся в отношении R' (см. рис. 6.2.), т.е. (аRb влечет Г(а)RГ(b) для любых а,bА). (аRb влечет Г(а)RГ(b) для любых а,bА).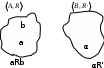 Рисунок 6.2. Определение 6. 7. Если при этом отображение  является взаимно однозначным соответствием, оно называется изоморфизмом модели является взаимно однозначным соответствием, оно называется изоморфизмом модели 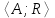 на модель на модель  . В этом случае существует и обратное отображение . В этом случае существует и обратное отображение 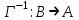 , также являющееся изоморфизмом: αR'β влечет Г-1(α)RГ-1(β) для любых α,βВ. При этом модели , также являющееся изоморфизмом: αR'β влечет Г-1(α)RГ-1(β) для любых α,βВ. При этом модели 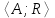 и и  называются изоморфными. называются изоморфными.Понятие гомоморфизма (изоморфизма) для алгебраических структур вводится аналогично тому, как это сделано для алгебр и моделей, при этом должны выполняться условия сохранения и операций, и отношений. Понятие изоморфизма - одно из важнейших понятий в современной математике. Так, из условия изоморфизма следует, например, что любое эквивалентное соотношение в алгебре A сохраняется в любой изоморфной ей алгебре A. Это позволяет, получив такие соотношения в алгебре A автоматически распространить их на все алгебры, изоморфные A. В частности, изоморфизм сохраняет свойства ассоциативности, коммутативности и дистрибутивности операций, а также рассматриваемые выше свойства отношений. Важным примером изоморфных алгебр являются так называемые булевы алгебры, в том числе: 1) β(U), {∩, U, -} - булева алгебра множеств. Здесь β(U) - множество всех подмножеств (булеан) множества U; {∩, U, -} - соответственно операции пересечения, объединения, дополнения над множествам 2) {Βη; &, ν, -} - булева алгебра двоичных векторов длины η. Здесь Βη - множество всех двоичных векторов длины η, т.е. Βη=ВВ...В=Вn, где В={0,1}; 3) {&, ν, -} - операции логического (покомпонентного) умножения, сложения и дополнения соответственно, определенные следующим образом: для любых векторов α=(α1,α2,...,αη) и β=(β1,β2,...,βη): α)α&β=(α1&β1,α2&β2,...,αη&βη), при этом α1&β1=1, если αi= βi=1, и αi&βi=Ο - в любом другом случае, т.е. если αi=1 и βi=1, αi&βi=1, αi&βi=Ο - в противном случае; Изоморфизм булевых алгебр широко используется в компьютерных вычислениях, например при необходимости выполнения операций над множествами с применением соответствующих и легко реализуемых на компьютере поразрядных операций над соответствующими двоичными векторами. Пример. Пусть Μ1 - множество сотрудников организации и R1, - заданное на нем отношение "быть старше" ( |
1. Определим отображение Г: Μ1,-> М2 следующим образом: каждому сотруднику организации из Μ1 поставим в соответствие Г число из М2, соответствующее его возрасту (в годах). Установленное таким образом отображение Г: М1, →М2 является гомоморфизмом моделей A= (М1,
2. Однако установленное отображение Г: М1 → М2 не является изоморфизмом моделей A=(М1;
