лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Графическое представление операцийДля нечетких множеств можно строить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значения µA(x), на оси абсцисс в произвольном порядке расположены элементы E. Если E по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами. 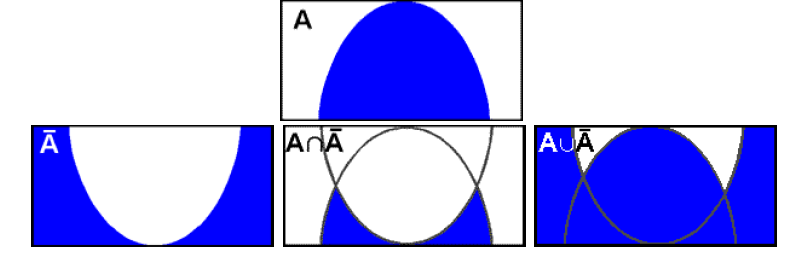 На верхней части рисунка заштрихованная часть соответствует нечеткому множеству A и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в A. На нижней - даны На верхней части рисунка заштрихованная часть соответствует нечеткому множеству A и, если говорить точно, изображает область значений А и всех нечетких множеств, содержащихся в A. На нижней - даны 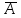 , , 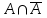 , , 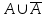 . .Тема 8. Алгебраические операции над нечеткими множествами.Определение 8.1. Алгебраическое произведение A и B обозначается A⋅B и определяется так: 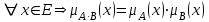 . .Определение 8.2. Алгебраическая сумма этих множеств обозначается 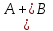 и определяется так: и определяется так: 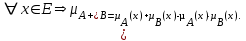 Для операций 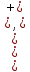 выполняются свойства: выполняются свойства: 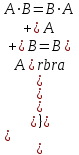 - коммутативность; - коммутативность; 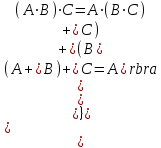 - ассоциативность; - ассоциативность;  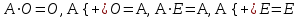 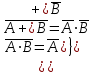 - теоремы де Моргана. - теоремы де Моргана.Не выполняются: 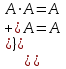 - идемпотентность; - идемпотентность; - дистрибутивность; - дистрибутивность; а также 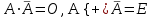 , , Для примера докажем свойство: 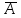 . Обозначим µA(x) через a, µB(x) через b. Тогда в левой части для каждого элемента х имеем: 1-ab, а в правой: (1-a)+(1-b)-(1-a)(1-b)=1 – a+1-b-1+a+b-ab=1-ab. Докажем, что свойство дистрибутивности не выполняется, т.е. . Обозначим µA(x) через a, µB(x) через b. Тогда в левой части для каждого элемента х имеем: 1-ab, а в правой: (1-a)+(1-b)-(1-a)(1-b)=1 – a+1-b-1+a+b-ab=1-ab. Докажем, что свойство дистрибутивности не выполняется, т.е. 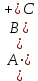 . Для левой части имеем: a(b+c-bc)=ab+ac-abc; для правой: ab+ac-(ab)(ac)=ab+ac+a2bc. Это означает, что дистрибутивность не выполняется при a≠a2. . Для левой части имеем: a(b+c-bc)=ab+ac-abc; для правой: ab+ac-(ab)(ac)=ab+ac+a2bc. Это означает, что дистрибутивность не выполняется при a≠a2.Замечание. При совместном использовании операций {∪, ∩,+,⋅} выполняются свойства: А⋅(BC)=(A⋅B)(A⋅C); А⋅(BC)=(A⋅B)(A⋅C); А (BC)=(A⋅B)(A⋅C); А⋅(BC)=(A⋅B)(A⋅C). Продолжим обзор основных операций над нечеткими множествами. На основе операции алгебраического произведения (по крайней мере, для целых α эта основа очевидна) определяется операция возведения в степень α нечеткого множества A, где α - положительное число. Нечеткое множество Aα определяется функцией принадлежности µAα=µαA(x). Частным случаем возведения в степень являются: CON(A)=A2 - операция концентрирования, DIL(A)=A0,5 - операция растяжения, которые используются при работе с лингвистическими неопределенностями. 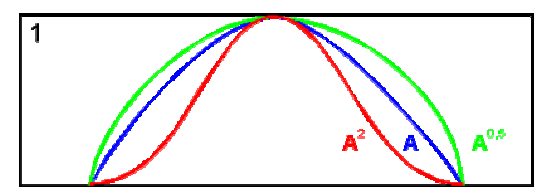 Определение 8.3. Умножение на число. Если α - положительное число, такое, что 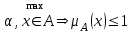 Выпуклая комбинация нечетких множеств. Пусть A1, A2,.., An - нечеткие множества универсального множества E, а ω1,ω2,...,ωn - неотрицательные числа, сумма которых равна 1. Определение 8.4.Выпуклой комбинацией A1, A2,.., An называется нечеткое множество A с функцией принадлежности: 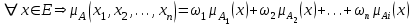 . .Декартово произведение нечетких множеств. Определение 8.5.Пусть A1, A2, ..., An - нечеткие подмножества универсальных множеств E1,E2,...,En соответственно. Декартово произведение A=A1×A2 × ...×An является нечетким подмножеством множества E=E1×E2×...×En с функцией принадлежности: 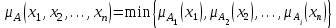 . .Определение 8.6.Оператор увеличения нечеткости используется для преобразования четких множеств в нечеткие и для увеличения нечеткости нечеткого множества. Пусть A - нечеткое множество, E - универсальное множество и для всех x∈E определены нечеткие множества K(х). Определение 8.7.Совокупность всех K(х) называется ядром оператора увеличения нечеткости Ф. Результатом действия оператора Ф на нечеткое множество A является нечеткое множество вида: 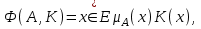 где µA(x)K(х) - произведение числа на нечеткое множество. где µA(x)K(х) - произведение числа на нечеткое множество. Пример: E = {1,2,3,4}; A = 0,8/1+0,6/2+0/3+0/4; K(1) = 1/1+0,4/2; K(2) = 1/2+0,4/1+0,4/3; K(3) = 1/3+0,5/4; K(4) = 1/4. Тогда Ф(A,K) = µA(1) K(1) ∪µA(2)K(2) ∪µA(3)K(3) ∪µA(4)K(4) = 0,8(1/1+0,4/2) ∪ 0,6(1/2+0,4/1+0,4/3) = 0,8/1+0,6/2+0,24/3. Определение 8.8.Четкое множество α-уровня (или уровня α). Множеством α-уровня нечеткого множества A универсального множества E называется четкое подмножество Aα универсального множества E, определяемое в виде: Aα ={x/µ A(x)≥α}, где α≤1. Пример: A = 0,2/x1 + 0/x2 + 0,5/x3 + 1/x4 , тогда A0.3 = {x3,x4}, A0.7 = {x4}. Достаточно очевидное свойство: если α1 ≥α2 , то Aα1≤ Aα2 . Теорема о декомпозиции. Всякое нечеткое множество A разложимо по его множествам уровня в виде: 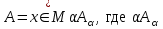 - произведение числа α на множество A, и α "пробегает" область значений M функции принадлежности нечеткого множества A. Пример: - произведение числа α на множество A, и α "пробегает" область значений M функции принадлежности нечеткого множества A. Пример: A = 0,1/x1 + 0/x2 + 0,7/x3 + 1/x4 представимо в виде: A = 0,1(1,0,1,1) ∪ 0,7(0,0,1,1,) ∪ 1(0,0,0,1)= = (0,1/x1 + 0/x2 + 0,1/x3 + 0,1/x4)∪ (0/x1 + 0/x2 + 0,7/x3 + 0,7/x4)∪ ∪(0/x1 + 0/x2 + 0/x3 + 1/x4) = 0,1/x1 +0/x2 +0,7/x3 +1/x4 . Если область значений функции принадлежности состоит из n градаций α1≤ α2≤ α3≤ ...≤ αn, то A (при фиксированных значениях градаций) представимо в виде: 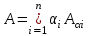 , т.е. определяется совокупностью обычных множеств { Aα1, Aα2, ..., Aαi}, где Aα1 ≥Aα2≥ , ..., ≥Aαi. , т.е. определяется совокупностью обычных множеств { Aα1, Aα2, ..., Aαi}, где Aα1 ≥Aα2≥ , ..., ≥Aαi. |
