лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Операция произведения графов.Пусть G1(X,E1) и G2(Y,E2) - два графа. Определение 11.7. Произведением G1G2 графов G1 и G2 называется граф с множеством вершин XY, а дуга из вершины (xi,yj) в вершину (xk,yl) существует тогда и только тогда, когда существуют дуги (xi,xk) E1 и (yj,yl) E2. Выполнение операции произведения рассмотрим на примере графов, изображенных на рис. 5. Множество вершин Z результирующего графа определяется как декартово произведение множеств XY. Множество Z содержит следующие элементы: z1=(x1y1), z2=(x1y2), z3=(x1y3), z4=(x2y1), z5=(x2y2), z6=(x2y3). Определим множество дуг результирующего графа. Для удобства рассмотрения составим таблицу, в первом столбце которой указываются дуги графа G1, во втором – дуги графа G2, а в третьем и четвертом – дуги результирующего графа.
Результирующий граф G1G2 изображен на рис.11.5. 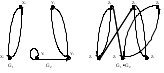 Рисунок 11.5. Операция произведения обладает следующими свойствами. 1. G1G2 = G2G1. 2. G1(G2G3) = (G1G2)G3. Рассмотрим выполнение операции произведения графов в матричной форме. Пусть G1(X,E1) и G2(Y,E2) – два графа, имеющие nx и ny вершин соответственно. Результирующий граф G1G2 имеет nxny вершин, а его матрица смежности вершин - квадратная матрица размером (nxny) (nx ny). Обозначим через a= a(ij)(kl) элемент матрицы смежности вершин, указывающий на наличие дуги (ребра), соединяющей вершину z=(xiyj) c z=(xkyl). Этот элемент может быть вычислен при помощи матриц смежности вершин исходных графов следующим образом: a=a(ij)(kl) = a1,ik a2,jl, (3) де a1,ik, a1,ik – элементы матрицы смежности вершин графов G1 и G2 соответственно. Пример. Выполнить операцию произведения на графах, приведенных на рис. 5. Составим матрицы смежности вершин исходных графов.
Построим матрицу A смежности вершин результирующего графа, каждый элемент которой вычисляется согласно соотношению (4.3).
Для удобства рассмотрения разделим матрицу A на четыре квадратные подматрицы. Заметим, что каждая подматрица может быть получена путем логического элементов матрицы умножения A2 на один из элементов a1,ijматрицы A1. С учетом этого матрицу A можно представить так:
Таким образом, матрица смежности вершин графа G1G2 имеет вид:
Нетрудно убедиться, что полученной матрице смежности вершин соответствует граф G1G2, представленный на рис. 11.5. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
