лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4

• Название: Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
• Анкор: лекции по дм
• Дата: 08.02.2021
• Размер: 1.51 Mb.
• Имя файла: лекции.docx
• Тип: Документы; #174835
• страница: 27 из 40

Алгоритм Флойда

Алгоритм Флойда находит кратчайшие пути между всеми парами вершин (узлов) в (ор)графе. В этом алгоритме для хранения информации о путях используется матрица Н: array [1..p,1..p] of 1..p, где



Алгоритм Флойда

Вход: матрица С[1..p,1..p] длин дуг.

Выход: матрица Т[1..p,1..p] длин путей и матрица Н[1..p,1..p] самих путей

for i from 1 to p do

for j from 1 to p do

T[i,j]:=C[i,j] {инициализация}

if C[i,j]=∞ then

H[i,j]:=0 {нетдугииз i в j}

else

H[i,j]:=j {естьдугаиз i в j}

end if

end for

end for

for i from 1 to p do

for j from 1 to p do

for k from 1 to p do

if i≠j & T[j,i]≠∞ & i≠k & T[i,k]≠∞ & (T[j,k]=∞VT[j,k]>T[j,i]+T[i,k])

then

H[j,k]:=H[j,i] {запомнить новый путь}

T[j,k]:=T[j,i]+T[i,k] {иегодлину}

end if

end for

end for

for j from 1 to p do

ifT[j,j]<0 then

stop {нет решения: вершина j входит в цикл отрицательной длины}

end if

end for

end for
Матрица H размера О(р²) хранит информацию обо всех (кратчайших) путях в графе. Заметим, что всего в фафе О(р²) путей, состоящих из О(р) вершин. Таким образом, непо­средственное представление всех путей потребовало бы памяти объема О(р³). Экономия памяти достигается за счет интерпретации представления, тоесть динамического вычис­ления некоторой части информации вместо её хранения в памяти. В данном случае любой конкретный путь <u,v> легко извлекается из матрицы с помощью следующего алгоритма.

w:=u; yield {первая вершина}

while w≠u do

w:=H[w,u]; yield w {следующая вершина}

end while
Если в G есть цикл с отрицательным весом, то решения поставленной задачи не существует, так как можно «накручивать» на этом цикле сколь угодно короткий путь.

Алгоритм Флойда имеет много общего с алгоритмом Уоршала. Покажем по индукции, что после выполнения i-го шага основного цикла по i элементы матриц T[j,k] и H[j,k] содержат, соответственно, длину кратчайшего пути и первую вершину на кратчайшем пути из вершины j в вершину k, проходящем через промежуточные вершины из диапазона 1..i. База: i=0, то есть до начала цикла элементы матриц T и H содержат информацию о кратчайших путях (если таковые есть), не проходящих ни через какие промежуточные вершины. Пусть теперь перед началом выполнения тела цикла на i-том шаге T[j,k] содержит длину кратчайшего пути от j к k, а H[j,k] содержит первую вершину на кратчайшем пути из вершины j в вершину k (если таковой есть). В таком случае, если в результате добавления вершины i к диапазону промежуточных вершин находится более короткий путь (в частности, если это вообще первый найденный путь), то он записывается. Таким образом после окончания цикла, когда i=p, матрицы содержат кратчайшие пути, проходящие через промежуточные вершины 1..p, то есть искомые кратчайшие пути. Алгоритм не всегда выдает решение, поскольку он не всегда существует. Дополнительный цикл по j служит для прекращения работы в случае обнаружения в графе цикла с отрицательным весом.

Алгори́тм Де́йкстры

Алгори́тм Де́йкстры (Dijkstra’s algorithm) — алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его использует протокол OSPF для устранения кольцевых маршрутов. Известен также под названием Сначала Кратчайший Путь (Shortest Path First).

Примеры

Вариант 1. Дана сеть автомобильных дорог, соединяющих города Новосибирской области. Некоторые дороги односторонние. Найти кратчайшие пути от Новосибирска до каждого города области (если двигаться можно только по дорогам).

Вариант 2. Имеется некоторое количество авиарейсов между городами мира, для каждого известна стоимость. Стоимость перелёта из A в B может быть не равна стоимости перелёта из B в A. Найти маршрут минимальной стоимости (возможно, с пересадками) от Копенгагена до Барнаула.

Формальное определение

Дан взвешенный ориентированный граф G(V,E) без петель и дуг отрицательного веса. Найти кратчайшие пути от некоторой вершины a графа G до всех остальных вершин этого графа.

Неформальное объяснение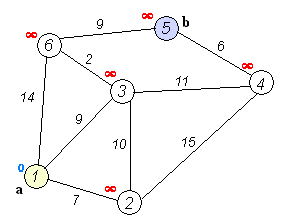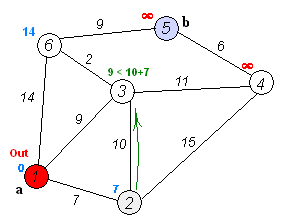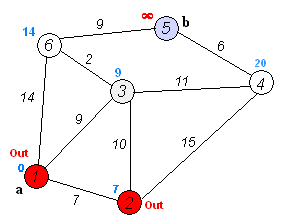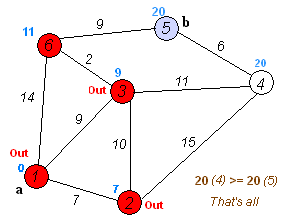



Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.

Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.

Пример

Рассмотрим выполнение алгоритма на примере графа, показанного на рисунке. Пусть требуется найти расстояния от 1-й вершины до всех остальных.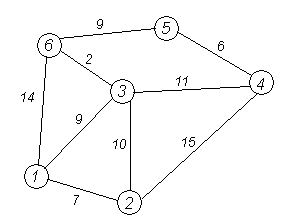



Кружками обозначены вершины, линиями — пути между ними (ребра графа). В кружках обозначены номера вершин, над ребрами обозначена их «цена» — длина пути. Рядом с каждой вершиной красным обозначена метка — длина кратчайшего пути в эту вершину из вершины 1.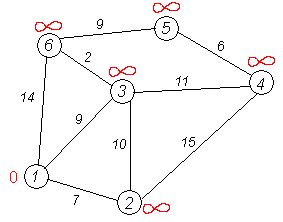



Первый шаг. Рассмотрим шаг алгоритма Дейкстры для нашего примера. Минимальную метку имеет вершина 1. Её соседями являются вершины 2, 3 и 6.



Первый по очереди сосед вершины 1 — вершина 2, потому что длина пути до неё минимальна. Длина пути в неё через вершину 1 равна сумме кратчайшего расстояния до вершины 1, значение её метки, и длины ребра, идущего из 1-ой в 2-ую, то есть 0 + 7 = 7. Это меньше текущей метки вершины 2, бесконечности, поэтому новая метка 2-й вершины равна 7.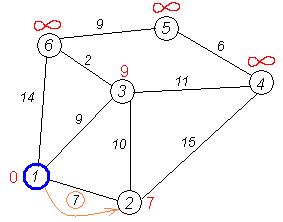



Аналогичную операцию проделываем с двумя другими соседями 1-й вершины — 3-й и 6-й.



Все соседи вершины 1 проверены. Текущее минимальное расстояние до вершины 1 считается окончательным и пересмотру не подлежит (то, что это действительно так, впервые доказал Э. Дейкстра). Вычеркнем её из графа, чтобы отметить, что эта вершина посещена.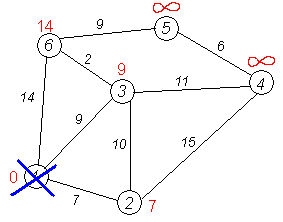



Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой 7.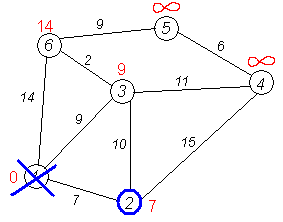



Снова пытаемся уменьшить метки соседей выбранной вершины, пытаясь пройти в них через 2-ю вершину. Соседями вершины 2 являются вершины 1, 3 и 4.

Первый (по порядку) сосед вершины 2 — вершина 1. Но она уже посещена, поэтому с 1-й вершиной ничего не делаем.

Следующий сосед вершины 2 — вершина 3, так имеет минимальную метку из вершин, отмеченных как не посещённые. Если идти в неё через 2, то длина такого пути будет равна 17 (7 + 10 = 17). Но текущая метка третьей вершины равна 9<17, поэтому метка не меняется.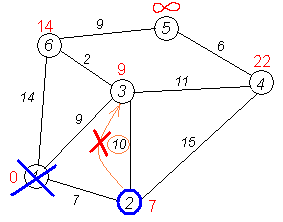




Ещё один сосед вершины 2 — вершина 4. Если идти в неё через 2-ю, то длина такого пути будет равна сумме кратчайшего расстояние до 2-ой вершины и расстояния между вершинами 2 и 4, то есть 22 (7 + 15 = 22). Поскольку 22< , устанавливаем метку вершины 4 равной 22.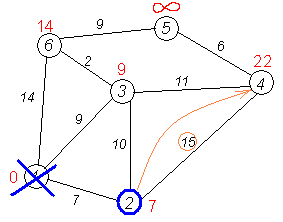



Все соседи вершины 2 просмотрены, замораживаем расстояние до неё и помечаем её как посещенную.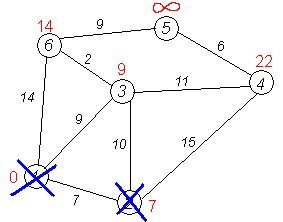



Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим такие результаты: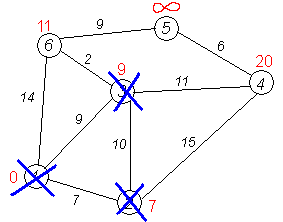



Дальнейшие шаги. Повторяем шаг алгоритма для оставшихся вершин. Это будут вершины 6, 4 и 5, соответственно порядку.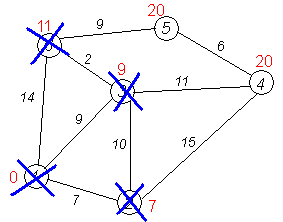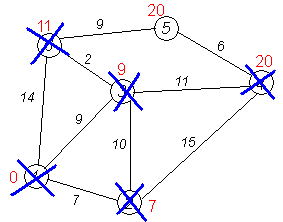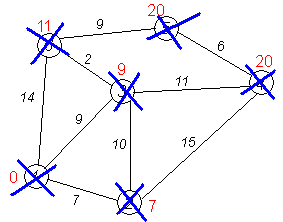






Завершение выполнения алгоритма. Алгоритм заканчивает работу, когда вычеркнуты все вершины. Результат его работы виден на последнем рисунке: кратчайший путь от вершины 1 до 2-й составляет 7, до 3-й — 9, до 4-й — 20, до 5-й — 20, до 6-й — 11.

Алгоритм

Обозначения

• 
  V — множество вершин графа
  
• 
  E — множество ребер графа
  
• 
  w[ij] — вес (длина) ребра ij
  
• 
  a — вершина, расстояния от которой ищутся
  
• 
  U — множество посещенных вершин
  
• 
  d[u] — по окончании работы алгоритма равно длине кратчайшего пути из a до вершины u
  
• 
  p[u] — по окончании работы алгоритма содержит кратчайший путь из a в u
  

Псевдокод

Присвоим

Для всех отличных от a

присвоим

Пока

Пусть — вершина с минимальным d[v]

Для всех таких, что

если d[u] > d[v] + w[vu] то

изменим

изменим

Описание

В простейшей реализации для хранения чисел d[i] можно использовать массив чисел, а для хранения принадлежности элемента множеству U — массив булевых переменных.

В начале алгоритма расстояние для начальной вершины полагается равным нулю, а все остальные расстояния заполняются большим положительным числом (бо́льшим максимального возможного пути в графе). Массив флагов заполняется нулями. Затем запускается основной цикл.

На каждом шаге цикла мы ищем вершину с минимальным расстоянием и флагом равным нулю. Затем мы устанавливаем в ней флаг в 1 и проверяем все соседние с ней вершины. Если в ней расстояние больше, чем сумма расстояния до текущей вершины и длины ребра, то уменьшаем его. Цикл завершается когда флаги всех вершин становятся равны 1, либо когда у всех вершин c флагом 0 . Последний случай возможен тогда и только тогда, когда граф G не связан.
Доказательство правильности

Пусть l(v) — длина кратчайшего пути из вершины a в вершину v. Докажем по индукции, что в момент посещения любой вершины z, d(z)=l(z).
База. Первой посещается вершина a. В этот момент d(a)=l(a)=0.
Шаг. Пускай мы выбрали для посещения вершину . Докажем, что в этот момент d(z)=l(z). Для начала отметим, что для любой вершины v, всегда выполняется (алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть P — кратчайший путь из a в z, y — первая непосещённая вершина на P, x — предшествующая ей (следовательно, посещённая). Поскольку путь P кратчайший, его часть, ведущая из a через x в y, тоже кратчайшая, следовательно l(y)=l(x)+w(xy). По предположению индукции, в момент посещения вершины x выполнялось d(x)=l(x), следовательно, вершина y тогда получила метку не больше чем d(x)+w(xy)=l(x)+w(xy)=l(y). Следовательно, d(y)=l(y). С другой стороны, поскольку сейчас мы выбрали вершину z, её метка минимальна среди непосещённых, то есть . Комбинируя это с , имеем d(z)=l(z), что и требовалось доказать.

Поскольку алгоритм заканчивает работу, когда все вершины посещены, в этот момент d=l для всех вершин.

Сложность алгоритма

Сложность алгоритма Дейкстры зависит от способа нахождения вершины v, а также способа хранения множества непосещенных вершин и способа обновления меток. Обозначим через n количество вершин, а через m — количество ребер в графе G.

• 
  В простейшем случае, когда для поиска вершины с минимальным d[v] просматривается все множество вершин, а для хранения величин d — массив, время работы алгоритма есть O(n² + m). Основной цикл выполняется порядка n раз, в каждом из них на нахождение минимума тратится порядка n операций, плюс количество релаксаций (смен меток), которое не превосходит количества ребер в исходном графе.
  

• 
  Для разреженных графов (то есть таких, для которых m много меньше n²) непосещенные вершины можно хранить в двоичной куче, а в качестве ключа использовать значения d[i], тогда время извлечения вершины из станет logn, при том, что время модификации d[i] возрастет до logn. Так как цикл выполняется порядка n раз, а количество релаксаций не больше m, скорость работы такой реализации O(nlogn + mlogn)
  

• 
  Если для хранения непосещенных вершин использовать фибоначчиеву кучу, для которой удаление происходит в среднем за O(logn), а уменьшение значения в среднем за O(1), то время работы алгоритма составит O(nlogn + m). Однако, согласно сайту intuit.ru,
  

скрытые константы в асимптотических оценках трудоемкости велики и использование фибоначчиевых куч редко оказывается целесообразным: обычные двоичные (d-ичные) кучи на практике эффективнее.

Альтернативами им служат толстые кучи, тонкие кучи и кучи Бродала, обладающие теми же асимптотическими оценками, но меньшими константами.

Тема 15. Свободные деревья. Основные свойства деревьев. Ориентированные, упорядоченные и бинарные деревья. Представление в ЭВМ свободных, ориентированных и упорядоченных деревьев.