лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Понятие минимизации булевых функций.Необходимо решить задачу простейшего представления функций алгебры логики, т. е. Решить задачу минимизации. Для этого необходимо указать: 1) Базис логических функций; 2)Представление функций в выбранном базисе; 3) Критерии минимизации представления функции в данном базисе. Если не задано дополнительное условие, то используют стандартный базис И, ИЛИ, НЕ. Функцию представляют в ДНФ или КНФ. Элементарную дизъюнкцию в дальнейшем будем называть конъюнктивным термом, элементарную конъюнкцию – дизъюнктивным термом. Ранг терма – число переменных, входящих в данный терм. Длина формулы, находящейся в ДНФ или в КНФ – число термов, которые ее образуют. Минимальной ДНФ или КНФ называют такую форму, которая имеет наименьшую длину. Булева функция находится в минимальной ДНФ или КНФ, если она минимальный суммарный ранг термов. Минимальная форма не допускает никаких последующих упрощений. В общем случае существует несколько способов записи одной и той же функции. Сложность записи можно оценивать числом элементарных операций. Форма записи булевой функции, в которой использовано наименьшее число операций по сравнению с другими называют абсолютно минимальной в принятом базисе. Задачу поиска наиболее простой записи функции называют задачей минимизации. Пример: Состав устройства, реализуйщий булеву функцию обычно представляют как схему, соединяющие ячейки устройств. Пусть ячейки, реализующие булевы функции обозначают: И 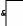 ИЛИ НЕ   Например: Изобразим схематично СДНФ функции (f2(х1, х2) – СДНФ): f2(х1, х2)=  1 х1 x1х2 1 х1 x1х2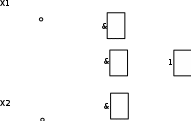 Тема 20. Геометрическая интерпретация минимизации. Метод неопределенных коэффициентов. Метод карт Карно Метод Петрика для нахождения тупиковых ДНФ.Геометрическая интерпретация минимизации функций алгебры логики.Для иллюстрации выполнения преобразований над булевыми функциями иногда удобно давать им геометрическое представление. Например, функцию f(x1,x2) удобно представлять на плоскости в системе координат x1,x2. Отложив единичные отрезки, получим квадрат, вершины которого соответствуют комбинациям переменных x1 и x2.  __________________ __________________ Пример: Пусть функция f(x1,x2) = x1,¬x2 v x1,x2. Из геометрических представлений следует, что две вершины, которые принадлежат одному и тому же ребру и называемые соседними, склеиваются по переменной, изменяющейся вдоль этого ребра. Это правило справедливо для конъюнктивных термов любого ранга, если они являются соседними для функции трех переменных, геометрическое представление имеет форму куба. Метод неопределённых коэффициентов.Предназначен для получения линейных форм логических формул, может быть применен для минимизации логических формул для любого числа переменных. В ручном варианте применяют для числа переменных не более пяти. Логическую функцию представляют в виде ДНФ. В общем виде, например, для трех переменных она имеет следующий вид: f(x1,x2,x3) = k11x1k01x1k12x2k02x2k13x3k03x3k1112x1x2k1012x1x2k12x1x2k0112x1x2k0012x1x2k1113x1x3k1013x1x3k0013x1x3k1123x2x3k1023x2x3k0123x2x3k0023x2x3k111123x1x2x3k110123x1x2x3k101123x1x2x3k100123x1x2x3k011123x1x2x3k010123x1x2x3k001123x1x2x3k000123x1x2x3 В этой дизъюнктивной норм. форме коэффициенты с индексами – это определенный коэффициент, принимающий значение 0 и 1 и подбирается таким образом, чтобы ДНФ была минимальная. Задавая различные наборы переменных x1,x2,x3 и приравнивая полученные выражения соответствующим значениям функции, получают систему уравнений для определения коэффициента к: f(0,0,0) = k01 k02 k03 k0012 k0023 k000123 f(0,0,1) = k01 k02 k13 k0012 k0113 k0123 k001123 …………………………………………… f(1,1,1) = k11 k12 k13 k1112 k1113 k1123 k111123 f(x1,x2,x3) = 0 1 Задание некоторой функции определяет значение первых частей системы: если f = 0 на соответствующем наборе переменных, то все коэффициенты входящие в уравнение, будут равны нулю. Это следует из свойства дизъюнкции. Тогда и в уравнении, где функция принимает единичное значение, надо вычеркивать все нулевые коэффициенты. Из оставшихся коэффициентов надо выбрать такой, который определяет темп наименьшего, и приравнять его к единице. А остальные коэффициенты приравнять к 0. Т.о. единичные коэффициенты определяют искомую ДНФ для системы уравнений. Рассмотрим f(x1,x2,x3) = F(0,2,4,7), так называется десятичная форма записи для логического выражения f(x1,x2,x3)= ,, , x2, x1,, x1, x2, x3 Для получения коэффициентов: 1) Выбрать строку, в которой функция равна нулю, и все коэффициенты приравнять к нулю. Если все нулевые строки просмотрены, то переходим к шагу 2. 2) Просмотрим строки, где функция равна еденице, и в этих строках вычеркиваем коэффициенты, которые принадлежат строкам с нулевым значением функции. 3) Переписывают все модифицированные уровнения. В полученной системе уравнений просматривают каждую строку и вычеркивают максимально возможное количество коэффициентов таким образом, чтобы ранг оставшихся терминов был минимальным. k0023 k0013 k0013 k0023 k000123=1 В модифицированной системе вычеркивают коэффициенты максимального ранга. Оставшиеся коэффициенты позволяют получить минимальную форму: f*(x1,x2,x3)= , , x1,x2,x3 |
