лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Тема 22. Законы алгебры логики в ОФПС и их следствия. Правило выполнения совместных логических действий, правило склеивания, правило поглощения, правило развертывания.В алгебре логики имеются четыре основных закона, регламентирующих порядок производства операций НЕ, И, ИЛИ в любом логическом выражении: переместительный (коммутативный); сочетательный (ассоциативный); распределительный (дистрибутивный); инверсии (правило Де Моргана). Переместительный закон. Этот закон справедлив как для дизъюнкции, так и для конъюнкции: x1 x2 = x2 x1; x1 x2 = x2 x1. (1) Справедливость выражения (1) нетрудно доказать простой подстановкой в него различных значений x1 и x2. Поскольку любую перестановку большего количества слагаемых можно свести к последовательности перестановок слагаемых в отдельных парах, то переместительный закон будет справедлив при любом числе слагаемых. Сочетательный закон. Этот закон, так же как и переместительный, является симметричным, т. е. справедливым и для дизъюнкции, и для конъюнкции: x1 x2 x3 = x1(x2 x3) = (x1 x2)x3= x2( x1 x3); (2) x1 x2 x3 = x1x2 x3) = (x1 x2)x3= x2( x1 x3). Доказательство этого закона также не представляет никаких трудностей и может быть выполнено простой подстановкой. Распределительный закон. В отличие от обычной алгебры алгебра логики симметрична. В ней справедливы два распределительных закона: для логического умножения относительно логического сложения (распределительный закон 1-го рода) и для логического сложения относительно логического умножения (распределительный закон 2-го рода). 1. Распределительный закон 1-го рода записывается следующим образом: (x1x2)x3=(x1x3) ( x2 x3) . (3) Справедливость формулы (3), а также и ее более общего случая, когда в скобках заключена сумма любого количества слагаемых, можно доказать путем установления идентичности условий обращения в 0 или 1 ее левой и правой частей. Условием обращения в нуль левой части выражения (3) состоит в том, чтобы нулю равнялся либо один аргумент х3, либо одновременно аргументы x1 и x2. Условия обращения в нуль правой части выражения (1) такие же. Следовательно, распределительный закон 1-го рода справедлив для алгебры логики. 2. Распределительный закон 2-го рода имеет вид (x1x2)x3=(x1x3) ( x2x3). (4) Справедливость формулы (4) (при любом количестве аргументов) нетрудно доказать посредством установления идентичности условий обращения обеих ее частей в единицу. Закон инверсии (правило Де Моргана). Этот закон, так же как и все предыдущие, симметричен относительно логических сложения и умножения. 1. Отрицание логической суммы нескольких аргументов равно логическому произведению отрицаний этих же аргументов: 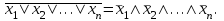 (5) (5)Доказательство закона не представляет трудностей, поскольку условие обращения в нуль как левой, так и правой частей выражения (5) состоит в том, чтобы был истинным хотя бы один аргумент. 2. Отрицание логического произведения нескольких аргументов равно логической сумме отрицаний этих же аргументов: 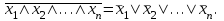 (6) (6)Справедливость этого закона следует из того, что условие обращения в единицу обеих частей формулы (6) заключается в том, чтобы был ложным хотя бы один аргумент. Следствия из законов алгебры логики. Из доказанных выше законов можно вывести ряд следствий, которые сформулируем в виде правил. Правило выполнения совместных логических действий (правило старшинства логических функций). При решении логических задач приходится встречаться с выражениями, содержащими действия отрицания, конъюнкции и дизъюнкции в любом сочетании. По аналогии с арифметическими действиями будем считать отрицание логическим действием первой ступени (старшей логической операцией), конъюнкцию - действием второй ступени, а дизъюнкцию - действием третьей ступени (младшей логической операцией). Старшинство операции инверсии вытекает из закона инверсии, в соответствии с которым логическая сумма отрицаний некоторых аргументов не равна отрицанию их суммы (это справедливо и для логического произведения). Это значит, что ни операцию дизъюнкции, ни операцию конъюнкции нельзя проводить, игнорируя знак отрицания над каким-либо из логических аргументов, т. е. операцию отрицания надо проводить в первую очередь. Относительно операций логического сложения и умножения на основании симметричности законов алгебры логики можно сказать, что они «равноправны». Из этого следует, что можно условиться считать более старшей операцией любую из них, но, приняв какое-либо условие, надо придерживаться его все время. На практике оказалось удобнее считать более старшей операцию логического умножения, так как это соответствует правилам обычной алгебры и для нас более привычно. На основе изложенного можно сформулировать следующее правило выполнения совместных логических действий: если в логическом выражении встречаются только действия одной и той же ступени, то их принято выполнять в том порядке, в котором они написаны; если в логическом выражении встречаются действия различных ступеней, то сначала принято выполнять действия первой ступени, затем -- второй, и только после этого -- третьей. Всякое отклонение от этого порядка должно быть обозначено скобками. Правило склеивания. Если имеется некоторый конечный набор логических аргументов x1, x2, … xn, то логическое произведение любого их числа называется элементарным в том случае, когда сомножителями в нем являются либо одиночные аргументы, либо отрицания одиночных аргументов. Так, например, f1(х1, х2, x3, х4)= х1 х2 x3х4-элементарное произведение (элементарная конъюнкция); --не является элементарным произведением. Символ любого аргумента в элементарной конъюнкции может встречаться только один раз, поскольку произведение аргумента самого на себя равно этому же аргументу, а произведение аргумента на свое отрицание равно нулю. Количество сомножителей в элементарной конъюнкции называется ее рангом. Два элементарных произведения одинакового ранга r называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из сомножителей. Например, элементарные конъюнкции f1(х1, х2, x3, х4)= х1 х2x3х4и f3(х1, х2, x3, х4)=  являются соседними, так как отличаются только одной инверсией в переменной x2, а элементарные конъюнкции f3(х1, х2, x3, х4)=  и f4(х1, х2, x3, х4)= и f4(х1, х2, x3, х4)= 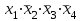 соседними не являются. Правило склеивания для элементарных конъюнкций может быть сформулировано следующим образом: логическую сумму двух соседних произведений некоторого ранга r можно заменить одним элементарным произведением ранга r-1, являющимся общей частью исходных слагаемых. Это правило является следствием распределительного закона 1-го рода и доказывается путем вынесения за скобку общей части слагаемых, являющихся соседними конъюнкциями. Тогда в скобках остается логическая сумма некоторого аргумента и его инверсии, равная единице, что и доказывает справедливость правила. Например, 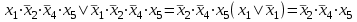 Поскольку алгебра логики является симметричной, то все определения, данные для конъюнкции, будут справедливы и для дизъюнкции. Если имеется некоторый конечный набор логических аргументов, то логическая сумма (дизъюнкция), зависящая от любого их числа, называется элементарной в том случае, когда слагаемыми в ней являются либо одиночные аргументы, либо отрицания одиночных аргументов. Количество слагаемых в элементарной дизъюнкции называется ее рангом. Две элементарные суммы одинакового ранга называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из слагаемых. Правило склеивания двух элементарных дизъюнкций формулируется так: логическое произведение двух соседних сумм некоторого ранга r можно заменить одной элементарной суммой ранга r-1, являющейся общей частью исходных сомножителей. Это правило является следствием распределительного закона 2-го рода и применяется для упрощения логических выражений. Например: 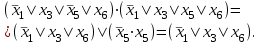 Правило поглощения. Так же как и склеивание, поглощение может быть двух видов. Правило поглощения для двух элементарных конъюнкций формулируется так: логическую сумму двух элементарных произведений разных рангов, из которых одно является собственной частью другого, можно заменить слагаемым, имеющим меньший ранг. Это правило является следствием распределительного закона 1-го рода. Доказывается оно посредством вынесения за скобку общей части слагаемых. В скобках останется логическая сумма некоторого выражения и единицы, равная в свою очередь также единице, что и доказывает справедливость правила. Например, 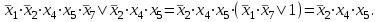 Правило поглощения для двух элементарных дизъюнкций: логическое произведение двух элементарных сумм разных рангов, из которых одна является общей частью другой, можно заменить сомножителем, имеющим меньший ранг. Это правило является следствием распределительного закона 2-го рода и также находит широкое применение для упрощения логических функций. Правило развертывания. Это правило регламентирует действие, обратное склеиванию. Иногда требуется представить некоторое логическое выражение в виде совокупности конституент единицы или конституент нуля. Если членами преобразуемого выражения являются элементарные конъюнкции, то переход от них к конституентам единицы производится в три этапа по следующему правилу: в развертываемую элементарную конъюнкцию ранга r в качестве дополнительных сомножителей вводится п-r единиц, где п -- ранг конституенты; каждая единица представляется в виде логической суммы некоторой, не имеющейся в исходной конъюнкции переменной и ее отрицания: ; производится раскрытие всех скобок на основе распределительного закона первого рода, что приводит к развертыванию исходной элементарной конъюнкции ранга r в логическую сумму конституент единицы. Пример. Развернуть элементарную конъюнкцию f(x1,x2,x3,x4) = =x1x3в логическую сумму конституент единицы. Решение. Ранг конституенты единицы для данной функции равен 4. Производим развертывание исходной конъюнкции поэтапно в соответствии с правилом развертывания: 1-й этап-- f(x1,x2,x3,x4) = x11x31. 2-й этап -- f(x1,x2,x3,x4) = 3-й этап -- f(x1,x2,x3,x4)= = что и требовалось получить. Если членами преобразуемого выражения являются элементарные дизъюнкции, то переход от них к конституентам нуля производится также в три этапа по следующему правилу: в развертываемую элементарную дизъюнкцию ранга r в качестве дополнительных слагаемых вводится п-r нулей; каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной дизъюнкции переменной, и ее отрицания: получившееся выражение преобразуется на основе распределительного закона второго рода таким образом, чтобы произвести развертывание исходной элементарной дизъюнкции ранга r в логическое произведение конституент нуля. Пример. Развернуть элементарную дизъюнкцию f(x1,x2,x3,x4)= =x3x4 влогическое произведение конституент нуля. Решение. Ранг конституенты нуля п = 4. Далее производим развертывание исходной дизъюнкции поэтапно в соответствии с правилом развертывания: 1-й этап -- f(x1,x2,x3,x4) =00x3x4; 2-й этап -- f(x1,x2,x3,x4) = 3-йэтап--f(x1,x2,x3,x4)= что и требовалось получить. Проверить правильность проведенных преобразований можно при помощи правила склеивания. |
