лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Тема 23. Задача анализа и синтеза логических схемПо заданной логической функции необходимо построить схему, реализующую данную функцию. Для построения логических схем элементы, предназначенные для логических операций необходимо располагать в порядке, указанном в выражении. Пусть задана функция: f2(х1, х2, х3)= 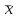 1x2 х3 x1x3 x1 x2 1x2 х3 x1x3 x1 x2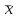 3x1x2х3. 3x1x2х3. 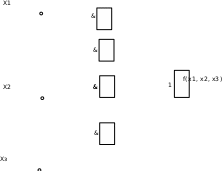 Синтез логических схем в заданном базисе С целью минимизации номенклатуры микросхем часто пользуются функционально полными системами из элементов: 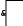  Штрих Шеффера Стрелка Пирса С помощью данных элементов можно выразить любую функцию. Задача анализа логической схемы По заданной логической схеме определить функцию, которую она реализует. Правила: Схема разбивается по ярусам справа налево. Начиная с последнего выхода, выходы каждого элемента обозначаются проиндексированными функциями ( индекс – номер яруса и номер элемента в ярусе). Записываются выходные функции каждого элемента в виде формулы с учетом введенных обозначений. Производится подстановка, используя входные элементы. Определение. Теория алгоритмов – раздел математики, который изучает общие свойства алгоритмов. Проблема теории – построение алгоритма, обладающего заданными свойствами. Такую проблему называют алгоритмической. Метрическая теория алгоритма исследует алгоритмы с точки зрения их сложности. Раздел известен как алгоритмическая сложность. Приложения имеются практически во всех разделах математики, во многих прикладных дисциплинах. Понятие алгоритма интерпретируют как точное описание, определенный процесс, набор вычислительных действий, соответствующих этому вычислительному процессу. Такое определение не является строгим, так как в нем используют произвольные данные. Определение является интуитивным. Среди других определений рассматривают определение Колмогорова. Определение. Алгоритм – всякая система вычислений по определенным данным, которые после числа шагов приводят к решению задачи. По Маркову: Алгоритм – точное предписание, определенный вычислительный процесс, варьирует исходные данные к результату. Определения не являются математически строгими и характеризуют набор свойств алгоритма. Свойства алгоритма: Дискретность информации. Каждый алгоритм имеет дело с входными, промежуточными, выходными данными, которые представлены в виде конечных слов в некотором формате. Дискретность работы алгоритма. Алгоритм выполняется по шагам. На каждом шаге выполняется только одна операция. Выполнимость операций. В алгоритме не должно быть невыполнимых операций. Конечность алгоритма. Описание алгоритма должно быть конечным. Детерминированность алгоритма. Каждый шаг алгоритма строго определен. После каждого шага указывается какой шаг сделать следующим или указывается, что алгоритм должен закончить работу. Массовость алгоритма. Алгоритм должен решать задачи из данного класса задач. Если найдется задача, для которой алгоритм не применим, то последовательность нельзя назвать алгоритмом. С развитием науки появились задачи, для которых не были найдены методы решений. Отсутствие алгоритма: недостаточность знаний или решения для алгоритма не существует. Для решения этой проблемы введена вычислительная функция. Пусть есть алгоритм α. Областью применимости α называют те объекты, которым он принадлежит. Говорят, что α вычисляет функцию f, если его область совпадает с D(f) и алгоритм α переработал элемент х их своей области применимости в область f(х). Функция f(х) называется вычислимой, если существует вычисляемый ее алгоритм. Данное определение не является строгим. Математики Клини и Черч строго определили математические функции, названные примитивно-рекурсивными. Черч высказал гипотезу, что множество рекурсивных совпадает со множеством вычислительных функций. Это получило название тезиса Чеча. Математики Пост и Тьюринг ввели понятие математической машины- абстрактная машина, которая механически вычисляет. Тезис Тьюринга: Для всякой вычислительной функции может быть построена машина Тьюринга. Для всякой рекурсивной функции может быть построена машина Тьюринга. Практический опыт показывает, что тесты являются верными, нет ни одного опровержения. Цели и задачи теории алгоритмов Обобщение результатов позволяет выделить цели и соотнесенные задачи: Формализация понятия алгоритма и исследование формальных алгоритмических систем. Формальные доказательства неразрешимости ряда задач. Классификация задач, исследование сложных классов. Алгоритмический анализ сложности алгоритма. Исследование и анализ рекурсивных алгоритмов. Получений явных функций трудоемкости алгоритма с целью их сравнительного анализа. Разработка критериев оценки качества алгоритма. Критерием качества называют признак, позволяющий оценивать качество разработанного алгоритма. Таким критерием является сложность. Чтобы оценка сложности была объективной, необходимо, чтобы оценка была количественной. Теоретики, оценивая сложность алгоритма, строят математическую модель машины Тьюринга. Тогда количество шагов для машины Тьюринга определяет его сложность. |
