лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Дизъюнктивная нормальная форма.Элементарной конъюнкцией называется такая формула A, которая является конъюнкцией, возможно одночленной, переменных и их отрицаний. Говорят, что формула A находится в дизъюнктивной нормальной форме (ДНФ), если она является дизъюнкцией, возможно одночленной, элементарных конъюнкций. ДНФ: A = x1 · x2 x1 · . Теорема о приведении формулы к ДНФ. AB, находящаяся в ДНФ, что A B. Bназывается ДНФ А. Доказательство: В качестве доказательства приводят алгоритм построения ДНФ формулы А. 1. С помощью основных равносильностей, которые позволяют устранить операции импликации и эквивалентности, строят 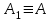 . При этом А1 не содержит операций импликации и эквивалентности. . При этом А1 не содержит операций импликации и эквивалентности.Основные равносильности: 1) 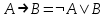 ; ; 2) 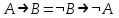 ; ; 3)  ; ; 4)  ; ; 5) 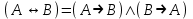 ; ; 6) 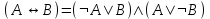 ; ;7) 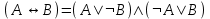 ; ; 8) 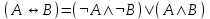 2. От А1 переходят к А2, в которой отрицание только перед переменной 1) A1 A 2) 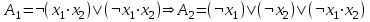 Полученная А2 равносильна А и состоит из многочисленных конъюнкций и дизъюнкций. К А2 применяют формулу дистрибутивности конъюнкции относительно дизъюнкции. Получим А3, находящуюся в дизъюнктивной нормальной форме. Рассмотрим конъюнкцию х1σ, х2σ2, ... , хnσn (1). Конъюнкция (1) называется конституентной единицей. Теорема. f(х1, х2,…, хn) может быть представлена в виде дизъюнкций конституент 1. На любом наборе f(х1, х2,…, хn)=1 будет равна 1 и только одна конституента. Дизъюнкция конституент равна 1, если 1 равна хотя бы 1 конституента. Пример
f1(х1, х2, х3)= 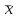 1 1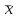 3 3 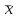 1 x2 x3 x1 x3x1x2 1 x2 x3 x1 x3x1x2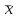 3. 3.f2(х1, х2, х3)= 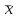 1x2 1x2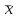 3 3 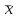 1 x2 x3 x1 x3x1x2х3. 1 x2 x3 x1 x3x1x2х3.Всякую конъюнкцию переменных функций функций, взятых с отрицанием, называют элементарной дизъюнкцией. Дизъюнкцию элементарных конъюнкций называют дизъюнктивной элементарной формой. |
