лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Представление в ЭВМ свободных, ориентированных и упорядоченных деревьев.Обсуждению представлений деревьев можно предпослать в точности те же рассуждения, что были предпосланы обсуждению представлений графов (см. раздел 7.4). Кроме того, следует подчеркнуть, что задача представления деревьев в программе встречается гораздо чаще, чем задача представления графов общего вида, а потому методы ее решения оказывают еще большее влияние на практику программирования. Представление свободных, ориентированных и упорядоченных деревьев. Всякое свободное дерево можно ориентировать, назначив один из узлов корнем. Всякое ордерево можно произвольно упорядочить. Всякое упорядоченное дерево можно представить бинарным деревом, проведя правую связь к старшему брату, а левую - к младшему сыну. Замечание: Рассматривается генеологическая терминология. Узлы, достижимые из узла называются потомками. Если в дереве существует дуга u, v, то узел u называют отцом, а узел v – сыном. Сыновья одного узла - братья Пример: На рис. приведены диаграммы упорядоченного и соответствующего ему бинарного деревьев. 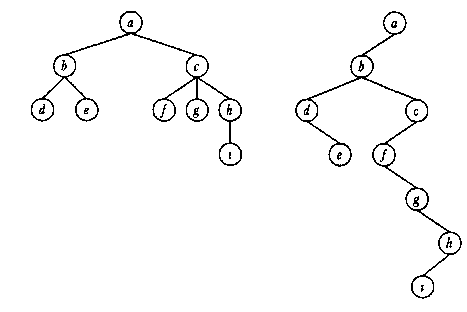 Таким образом, достаточно рассмотреть представление в ЭВМ бинарных деревьев. Замечание: Из данного представления следует, что множество бинарных деревьев взаимнооднозначно соответствует множеству упорядоченных лесов упорядоченных деревьев. Тема 16. Применение деревьев в программировании. Ассоциативная память. Выровненные деревья. Сбалансированные деревья. Минимальный каркас. Схема алгоритма построения минимального каркаса. Ориентированные и упорядоченные ориентированные деревья интенсивно используются в программировании. 1. Выражения. Для представления выражений языков программирования, как правило, используются ориентированные упорядоченные деревья. Пример представления выражения а + b · с показан на рисунке слева. 2. Для представления блочной структуры программы и связанной с ней структуры областей определения идентификаторов часто используется ориентированное дерево (может быть, неупорядоченное, так как порядок определения переменных в блоке в большинстве языков программирования считается несущественным). На рисунке в центре показана структура областей определения идентификаторов а, b, с, d, e, причем для отображения структуры дерева использована альтернативная техника. 3. Для представления иерархической структуры вложенности элементов данных и/или операторов управления часто используется техника отступов, показанная на рисунке справа.  4. Структура вложенности каталогов и файлов в современных операционных систе-мах является упорядоченным ориентированным деревом. 5. Различные "уравновешенные скобочные структуры" (например (a(b)(c(d)(e)))) являются ориентированными упорядоченными деревьями. Это отражается даже в терминологии – "корневой каталог диска". Замечание: Общепринятой практикой при изображении деревьев является соглашение о том, что корень находится наверху и все стрелки дуг ориентированы сверху вниз, поэтому стрелки можно не изображать. Таким образом, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми, и требуется дополнительное указание, дерево какого класса изображено на диаграмме. В большинстве случаев это ясно из контекста. Пример: На рис. 8.8 приведены три диаграммы деревьев, которые внешне выглядят различными. Обозначим дерево слева – (1), в центре – (2) и справа – (3). Как упорядоченные деревья, они все различны: (1) ^ (2), (2) ^ (3), (3) ^ (1). Как ориентированные деревья (1) = (2), но (2) ^ (3). Как свободные деревья, они все изоморфны: (1) = (2) = (3). Применение деревьев в программировании. Ассоциативная память. Выровненные деревья. Сбалансированные деревья.В практическом программировании для организации хранения данных и доступа к ним часто используется механизм, который называют ассоциативной памятью. При использовании ассоциативной памяти данные делятся на порции (записи), и с каждой записью ассоциируется ключ. Ключ – значение из некоторого вполне упорядоченного множества. Записи могут иметь произвольную природу и различные размеры. Доступ к данным осуществляется по ключу, который выбирают простым, компактным и удобным для работы. Пример: Пример ассоциативной памяти. Банковский счет: ключ – номер счета, запись – финансовая информация. Ассоциативная память должна поддерживать три основные операции: 1) Добавить (ключ, запись); 2) Найти (запись по ключу); 3) Удалить (ключ). Для представления ассоциативной памяти используют следующие структуры данных: 1) Неупорядоченный массив; 2) Упорядоченный массив; 3) Дерево сортировки (бинарное дерево, каждый узел которого содержит ключ и обладает следующим свойством: значение ключа во всех узлах левого поддерева меньше, а во всех узлах правого поддерева больше, чем значение ключа в узле). 4) Таблица расстановки, или хэш-таблица.  Бинарные деревья. Бинарное дерево - это конечное множество узлов, которое либо пусто, либо состоит из корня и двух непересекающихся бинарных деревьев - левого и правого. Бинарное дерево не является упорядоченным ордеревом. Пример: На рисунке приведены две диаграммы деревьев, которые изоморфны как упорядоченные, ориентированные и свободные деревья, но не изоморфны как бинарные деревья.  Основная идея таблицы расстановки состоит в том, что подбирается специальная функция, которая называется хэш-функцией, переводящая значение ключа в адрес хранения записи. Адресом может быть индекс в массиве, номер кластера на диске и т.д. Таким образом, имея ключ, с помощью хэш-функции сразу определяется место хранения записи и открывается доступ к ней. Эффективность ассоциативной памяти зависит от структуры используемых для ее представления данных. Дерево сортировки может расти неравномерно при реализации операций с ассоциативной памятью. Например, если при загрузке дерево исходных данных уже упорядочено, то полученное дерево будет право- или леволинейным и будет даже менее эффективно, чем неупорядоченный массив. Наибольший эффект при поиске дают выровненные деревья. Ордерево – выровненное, если все узлы, степень которых меньше 2, располагаются на одном или двух последних уровнях. Пример: На рисунке показаны диаграммы выровненного (а) и невыровненного (б) деревьев.  Бинарное дерево – сбалансированное (подровненное), если для каждого узла высота левого и правого поддеревьев отличается не более, чем на единицу. Сбалансированные деревья уступают выровненным деревьям по скорости поиска менее, чем в два раза. Однако их преимущество в том, что известны алгоритмы вставки и удаления узла из сбалансированного дерева, которые сохраняют сбалансированность и, в то же время, при перестройке дерева затрагивают только конечное число узлов. |
