лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Минимальный каркас. Схема алгоритма построения минимальных каркасов.Задача отыскания минимального каркаса (кратчайшего остова) – классическая задача теории графов. Методы решения этой задачи послужили основой многих других важных результатов (исследование алгоритма Краскала привели к созданию теории "жадных" алгоритмов). Пусть G(V,E) – граф. Остов (каркас) – остовной подграф, являющийся деревом. Несвязный граф не имеет остова, связный граф может иметь много остовов. Если задать длины ребер, то можно поставить задачу нахождения кратчайшего остова, или минимального каркаса. Пример: Пример практической интерпретации задачи нахождения кратчайшего остова. Пусть задано множество аэродромов, и нужно определить минимальный по сумме расстояний набор авиарейсов, который позволил бы перелетать с любого аэродрома на любой другой аэродром. Решение задачи – кратчайший остов полного графа расстояний между аэродромами. 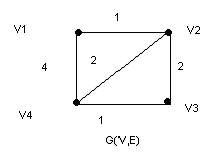 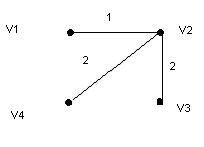 Граф расстояний между аэродромами и дерево кратчайших путей из вершины v1. 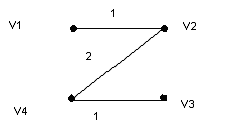 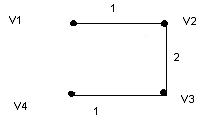 Кратчайшие остовы для графа G(V,E) Рассмотрим схему алгоритма построения кратчайшего остова. Пусть Т – множество непересекающихся деревьев, являющихся подграфами графа G. Вначале Т состоит из отдельных вершин графа G, в конце Т содержит единственный элемент – кратчайший остов графа G.Схема алгоритма. Вход: граф G(V,E), заданный матрицей длин ребер С. Выход: кратчайший остов Т. Т:=V while в Т больше одного элемента do взять любое поддерево из Т найти к нему ближайшее соединить эти деревья в Т end while Тема 17. Циклы и коциклы. Эйлеровы циклы. Гамильтоновы циклы. Теорема Дирака. Раскраска графов. Хроматическое число. Планарные графы. Укладка графов. Алгоритм раскрашивания. 21. Циклы и коциклы. Эйлеровы циклы. Гамильтоновы циклы. Теорема Дирака.Цикл может входить только в одну компоненту связности графов. k(G)=2 Следовательно, далее будем рассматривать связанные графы. Цикл (простой) рассматривается как множество рёбер. Разрез связного графа – это множество ребер, удаление которых делает граф не связным.  е1    С3 – {e1, e2}→k(G’)=2 е3 С3:  Простой разрез – это минимальный разрез, т.е. такой, никакое собственное подмножество которого разрезом не является. Между циклами и разрезами существует определенная двойственность. Следовательно, разрезы называют коциклами. Чем больше в графе циклов, тем труднее его разрезать. В дереве, напротив, каждое ребро является разрезом. Максимальное независимое множество циклов – это фундаментальная система циклов. Циклы фундаментальной системы называются фундаментальными, а количество циклов в данной фундаментальной системы – циклическим рангом, или циклическим числом. Обозначение: m(G). Максимальное независимое множество коциклов (разрезов) – фундаментальная система разрезов. Коциклы фундаментальной системы – фундаментальные, а количество коциклов в данной фундаментальной системе называется к-циклическим рангом, или коциклическим числом графа G. Обозначение: m*(G). Пусть T(V, ET) – остов графа G(V, T). Кодерево T*(V, ET*) остова T(V, GT) – такой подграф (остовный), что ET* = E / ET. Кодерево не является деревом. Ребра кодерева – хорды остова. Теорема 1. Если граф G – связный граф, то цикломатическое число определяется как: m(G) = q - p + 1, а коцикломатическое – как: m*(G) = p - 1. Если граф имеет цикл (не обязательно простой), содержащий все ребра графа по одному разу, то это Эйлеров цикл, а граф – Эйлеров граф. Если граф имеет цепь (не обязательно простую), содержащую все вершины по одному разу, то цепь – Эйлерова цепь, а граф – полуэйлеров граф. Эйлеров цикл содержит не только все ребра (по одному разу), но и все вершины графа (возможно по несколько раз). Эйлеровым может быть только связный граф. Теорема 2. Если граф G связен и не тривиален, то справедливы следующие утверждения: 1) Граф G – Эйлеров граф; 2) Каждая вершина графа G имеет четную степень. 3) Множество ребер графа G можно разбить на простые циклы. Чтобы убедится в наличии Эйлерова цикла, в графе необходимо и достаточно проверить, что степени всех вершин четные. 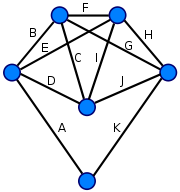 эйлеров граф Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл – Гамильтонов, а граф – Гамильтонов граф. Гамильтонов цикл не обязательно содержит все ребра графа. Гамильтоновым может быть только связный граф. Теорема 3 (теорема Дирака). Если в графе G(V, E) для любой вершины u из множества V d(u)іp / 2, то граф G – Гамильтонов.  гамильтонов граф |
