лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Примеры нечетких множествПример. Пусть E = {0,1,2,..,10}, M =[0,1]. Нечеткое множество "несколько" можно определить следующим образом: 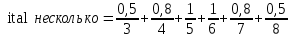 , его характеристики: высота = 1, носитель={3,4,5,6,7,8}, точки перехода - {3,8}. , его характеристики: высота = 1, носитель={3,4,5,6,7,8}, точки перехода - {3,8}. Пример. Пусть E = {0,1,2,3,...,n,...}. Нечеткое множество "малый" можно определить: “малый”= 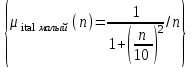 Пример. Пусть E = {1,2,3,...,100} и соответствует понятию "возраст", тогда нечеткое множество "молодой", может быть определено с помощью µ"молодой"(x)= 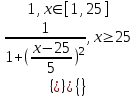 Нечеткое множество "молодой" на универсальном множестве E’={Иванов, Петров, Сидоров,...} задается с помощью функции принадлежности µ"молодой"(x) на E={1,2,3,..100} (возраст), называемой по отношению к E’ функцией совместимости, при этом: 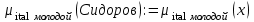 , где х – возраст Сидорова. , где х – возраст Сидорова.Операции над нечеткими множествамиВключение. Пусть A и B - нечеткие множества на универсальном множестве E. Говорят, что A содержится в B, если ∀x ∈E µA(x) µB(x). Обозначение: A⊂B. Иногда используют термин "доминирование", т.е. в случае когда A⊂B, говорят, что B доминирует A. Равенство. A и B равны, если ∀x∈E µA(x)=µB (x). Обозначение: 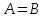 . . Дополнение. Пусть Μ=[0,1], A и B - нечеткие множества, заданные на E. A иB дополняют друг друга, если ∀x∈E µA(x) = 1 - µ B(x). Обозначение: 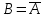 или или 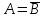 . .Очевидно, что 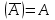 . (Дополнение определено для M=[0,1], но очевидно, что его можно определить для любого упорядоченного M). . (Дополнение определено для M=[0,1], но очевидно, что его можно определить для любого упорядоченного M). Пересечение. AB - наибольшее нечеткое подмножество, содержащееся одновременно в A, и в B. 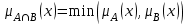 . .Объединение. АВ - наименьшее нечеткое подмножество, включающее как А, так и В, с функцией принадлежности: 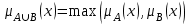 . .Разность. 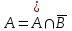 с функцией принадлежности: с функцией принадлежности: 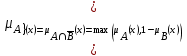 . .Дизъюнктивная сумма. 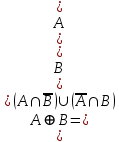 с функцией принадлежности: с функцией принадлежности: 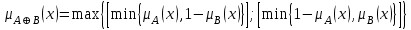 Примеры. Пусть: A = 0,4/ x1 + 0,2/ x2+0/ x3+1/ x4; B = 0,7/ x1+0,9/ x2+0,1/ x3+1/ x4; C = 0,1/ x1+1/ x2+0,2/ x3+0,9/ x4. Здесь: A⊂B, т.е. A содержится в B или B доминирует A, С несравнимо ни с A, ни с B, т.е. пары {A, С} и {A, С} - пары недоминируемых нечетких множеств. A ≠ B ≠ C. 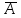 = 0,6/ x1 + 0,8/x2 + 1/x3 + 0/x4; = 0,6/ x1 + 0,8/x2 + 1/x3 + 0/x4; 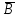 = 0,3/x1 + 0,1/x2 + 0,9/x3 + 0/x4. = 0,3/x1 + 0,1/x2 + 0,9/x3 + 0/x4. A∩B = 0,4/x1 + 0,2/x2 + 0/x3 + 1/x4. А∪В = 0,7/x1 + 0,9/x2 + 0,1/x3 + 1/x4. А - В = А∩ = 0,3/x1 + 0,1/x2 + 0/x3 + 0/x4; В\А = ∩ В = 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4. А ⊕ В = 0,6/x1 + 0,8/x2 + 0,1/x3 + 0/x4. |
