лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4

• Название: Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
• Анкор: лекции по дм
• Дата: 08.02.2021
• Размер: 1.51 Mb.
• Имя файла: лекции.docx
• Тип: Документы; #174835
• страница: 19 из 40

Расстояние между вершинами.

Определение 10.4. Расстояние между вершинами u и v обозначается d(u, v), называется длина кратчайшей цепи u, v. А сама кратчайшая цепь d(u, v) = min |<u, v>| называется геодезической.

Если между вершинами u, v не существует цепи, то d(u, v) = + ∞.

Пример:

d(v₁, v₂) = + ∞.

Диаметром графа G обозначается D(G), называется длина длиннейшей геодезической, или наибольшей из кратчайших путей.

Множество вершин, находящихся на расстоянии n от вершины v (т.е. D(v, n) = {u  U d(u, v) = n}

Связность.

Определение 10.5. Говорят, что две вершины связаны, если существует соединяющая их простая цепь.

Определение 10.6. Граф, в котором все вершины связаны – называют связным.

Отношение связанности вершин является эквивалентностью. Классы эквивалентности по отношению связанности называют компонентами связности графов. Число компонентов графа G обозначают k(G). Граф G является связным тогда и только тогда, когда k(G) = 1. Если k(G) > 1, то G – несвязный граф. Граф, состоящий только из изолированных вершин, в котором k(G) = p(G) и r(G) = 0 называют вполне несвязным графом.

Виды графов: тривиальные и полные графы, двудольные графы, орграфы и сети.

Определение 10.7. Граф, состоящий из одной вершины называется тривиальным.

Определение 10.8.Граф у которого любая пара вершин смежные называется полным графом.

Полный граф с Р вершинами обозначается k_p. Его максимальное количество ребер находится по формуле .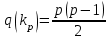

Пример.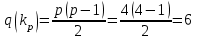

.

Действительно, можно заметить, что данный граф имеет 6 ребер.


Определение 10.9.Полный подграф некоторого графа называется кликой этого графа.

Граф, состоящий из простого цикла с k вершинами обозначается с_k.

Определение 10.10. Двудольным графом (биграфом, чётным графом) называется такой граф G(V,E), что , при чём всякое ребро из множества Е инцидентно вершине из V₁ и вершине из V₂. Множество из V₁ и V₂ называется долями этого графа

Определение 10.11. Если двудольный граф содержит все ребра, соединяющие множества V₁ и V₂, то такой граф называют полным двудольным графом.

Теорема. Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

Определение 10.11. Если в графе ориентировать все ребра, то получится направленный орграф.

Определение 10.12. Если в графе полустепень захода некоторой вершины равна 0 (d⁺=0), то такая вершина называется источником.

Определение 10.13. Если в графе полустепень исхода некоторой вершины равна 0 (d^-=0), то такая вершина называется стоком.

Определение 10.13. Направленный граф с одним истоком и одним стоком называется сетью.

Тема 11. Матрица смежности, матрица инцидентности. Операции над графами. Представление графов в ЭВМ.

Матрица смежности. Матрица инцедентности.

Определение 11.1. Представление графа с помощью квадратной матрицы, отражающей смежность вершин М: array [1..p,l..p] of [0..1] называется матрицей смежности, где

М[i ,j] =

Определение 11.2. Представление графа с помощью матрицы H: array [1..p, 1..q] of [0..1], отражающей инцидентность вершин и ребер, называется матрицей инциденций.

Для неориентированного графа:

H [i, j] =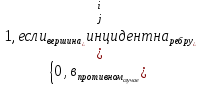

Для ориентированного графа используют матрицу Н: array [1..p, 1..p] of [-1..1]

H [i ,j] =

Операции над графами позволяют образовывать новые графы из нескольких более простых. В этом параграфе будут рассмотрены операции на графах без параллельных ребер (дуг).