лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4

• Название: Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
• Анкор: лекции по дм
• Дата: 08.02.2021
• Размер: 1.51 Mb.
• Имя файла: лекции.docx
• Тип: Документы; #174835
• страница: 8 из 40

Алгоритм топологической сортировки

Для упорядоченной пары элементов (a, b), элемент a будем называть предшественником, а элемент b преемником. Суть алгоритма заключается в следующем.

а) Для каждого элемента определяем его преемников и подсчитываем количество его предшественников. В дальнейшем работаем не с множеством элементов, каждому из которых приписан счетчик предшественников и список преемников.

б) Выбираем из построенного множества и помещаем в выходной список элементы, не имеющие предшественников (с нулевым счетчиком).

в) Каждое извлечение элемента (см. пункт б) сопровождаем пересчетом количества оставшихся предшественников. Причем, эта операция затрагивает только те элементы, которые являются преемниками удаляемого.

Пункты б) и в) повторяем до тех пор, пока это возможно. Если в очередной раз пункт б) не выполним, а множество непустое, то топологическая сортировка невозможна. Если же множество исчерпано, то топологическая сортировка выполнена "удачно" и в выходном списке перечислены элементы в допустимом порядке.

Операции над бинарными отношениями.

Так как отношения на X задаются подмножествами, aXX, для них определены те же операции, что и над множествами.

Возьмем два отношения α и . Каждому из них соответствует некоторое множество пар (подмножества aXX и XX).

Определение 3.14. Пересечением отношений α называется отношение, определяемое пересечением соответствующих подмножеств.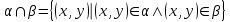



Ясно, что x(α)y выполнено тогда и только тогда, когда одновременно выполнены соотношения xαy и xy.

Пример. Пусть X - множество вещественных чисел, α - отношение "быть не меньше",  - отношение "быть строго больше". Тогда α есть отношение "быть строго больше".

Определение 3.15. Объединением отношений α называется отношение, определяемое объединением соответствующих множеств.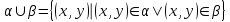



Соотношение x(α)y выполнено тогда и только тогда, когда выполнено хотя бы одно их соотношений xαy или xy.

Пример. Если α – отношение "больше" на множестве чисел, а  – отношение "равно", то α – это отношение ≥.

Определение 3.16. Обратным отношением называется отношение, определяемое условием: .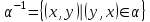

Пример. Пусть α – отношение "делит", тогда α^-1 – отношение "делится".

Определение 3.17. Разностью будем называть отношение, удовлетворяющее условию .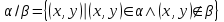

Определение 3.18. Разностью будем называть отношение, удовлетворяющее условию 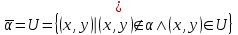, где U

Определение 3.19. Составное отношение (композицией) называется отношение, определяемое следующим образом: .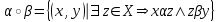

Пример. Пусть α – отношение "быть женой", а  – отношение "быть отцом". Что означает в этом случае соотношение хαу? По определению существует такой z, что "x - жена z" и "z - отец y". Другими словами, "x есть жена отца y", т.е. "x - мать или мачеха y".

Пример. Пусть α – отношение "быть братом", а  – отношение "быть родителем". Тогда произведение α есть отношение "быть братом одного из родителей", т.е. "быть дядей".

Лемма 3.2. Если отношения α и  рефлексивны, то рефлексивны и следующие отношения: α, α, α^-1, α.

Лемма 3.3. Если отношения α и  симметричны, то симметричны и следующие отношения: α, α, α^-1.

Лемма 3.4. Чтобы составное отношениеα симметричных отношений α и  было симметрично, необходимо и достаточно, чтобы отношения α и  коммутировали.

Лемма 3.5. Если отношения α и  – антисимметричны, то антисимметричны также и следующие отношения: α, α^-1.

Антисимметричность может не сохраняться при объединении и композиции.

Лемма 3.6. Если отношения α и  транзитивны, то транзитивны также следующие отношения: α, α^-1.

Из лемм 3.2, 3.3, 3.4, 3.5 вытекают следующие две теоремы.

Теорема 3.6. Если α и  – строгие порядки (нестрогие порядки), то пересечение α также является строгим порядком (нестрогим порядком).

Замечание. Пересечение строгого и нестрогого порядка есть строгий порядок.

Свойство "быть линейным порядком" не обязано сохраняться при пересечении. Это проще всего увидеть из следующих соображений. Пусть a – линейный порядок (строгий или нестрогий), тогда αα^-1= (или =E). Значит, αα^-1на множестве более чем из одного элемента не является линейным порядком.

Теорема 3.7. Если отношение α является строгим (нестрогим, линейным) порядком, то и отношение α^-1 является строгим (нестрогим, линейным) порядком.

Объединение порядков в общем случае не является порядком. Это хорошо видно на таком примере. Пусть α – линейный нестрогий порядок, тогда α^-1 – есть отношение того же типа. Однако, объединение αα^-1 есть полное отношение, и, следовательно, не является порядком. Ниже приведены без доказательства условия, при которых объединение порядков является порядком.

Теорема 3.8. Если α и  – строгие порядки, то объединение α является строгим порядком в том и только том случае, когда .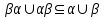

Теорема 3.9. Для того чтобы объединение α нестрогих порядков α и  было нестрогим порядком, необходимо и достаточно выполнение условий , .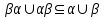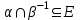

Композицией порядков α также не обязано быть порядком. Это видно из того хотя бы, что для линейного нестрогого порядка α композиция 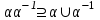есть полное отношение. Достаточным условием является, например, такое.

Теорема 3.10. Если α и  – строгие порядки и выполнены соотношения: 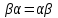, , то α – строгий порядок.