лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4

• Название: Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
• Анкор: лекции по дм
• Дата: 08.02.2021
• Размер: 1.51 Mb.
• Имя файла: лекции.docx
• Тип: Документы; #174835
• страница: 4 из 40

Упорядоченные пары. Декартово (прямое) произведение множеств. Отношения.

В предыдущем разделе операции над множествами давали множества той же природы. Например, если исходные множества были множествами чисел, то и полученные в результате операций множества были множествами чисел. В этом разделе мы определим операцию, с помощью которой меняется природа элементов получающихся множеств.

Определение 2.1. Упорядоченной парой (набор из 2 объектов) из элементов a и b (a,b), взятых именно в этом порядке, называется множество, состоящее из двух множеств, включающих элемент a: {a},{a,b}.

(a,b)= {{a},{a,b}}

Таким образом, понятие упорядоченной пары не выводит рассмотрение за пределы теории множеств. Но тем не менее независимое определение упорядоченной пары технически удобнее. Исходя из приведенного определения, доказывается справедливость следующей леммы:

Лемма: упорядоченные пары (a,b) и (c,d) равны тогда и только тогда, когда выполняется условие: (a,b) = (c,d) | a = с & b = d

Обобщением понятия упорядоченной пары является упорядоченный n-набор или картеж. В отличии от конечного множества {a₁, … a_n} картеж (a₁, … a_n) на множествах А₁, … А_n, характеризуется не только входящими в него элементами, но и порядком в котором они перечисляются, как и для упорядоченных пар роль порядка в картеже фиксируется определением равенства картежей.

Определение 2.2.Множество всех картежей длины n на множествах А₁, … А_n называется декартовым.

Пусть А и В – два множества.

Определение 2.3. Прямым (декартовым) произведением двух множеств А и В называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит множеству А, а второй множеству В.

Обозначают: АВ := {(а,b) | а А &bB}

Степенью множества А называется его прямое произведение самого на себя.

Соответственно: А¹:=A; А²:=AA; А³:=AA²; и вообще Аⁿ:=AA^n-1

Теорема: |АВ| = |А|  |В|

Доказательство:

Первый компонент упорядоченной пары можно выбрать |А| способами, второй - |В| способами (|А| - число элементов множества А; |В| - число элементов множества В.)

Таким образом, всего имеется |А|·|В| упорядоченных пар.

Пример 2.1.: А = {1,2,3}, |A| = 3; B = {4,5}, |B| = 2;

|АВ| = |А|  |В| = 3·2 = 6;

|АВ| = |{(1,4),(1,5),(2,4),(2,5),(3,4),(3,5)}| = 6;
Пусть А и В – два множества.

Определение 2.4. Бинарным отношением R из множества А в множество В называется подмножество прямого произведения: RAB.

Для бинарных отношений обычно используется инфиксная форма записи:

aRb:(a,b)RAB.

Если А = В, то говорят, что R есть отношение на множестве А и записывают RAА или RA².

Многоместные отношения. Композиция отношений. Степень и ядро отношений.

Понятие многоместного отношения является обобщающим понятием отношения и его называют n-местным или n-арным отношением.

Определение 2.5. n-местным отношением называется любое подмножество множества Аⁿ, где А – произвольное множество, n  1. Двухместное отношение называют бинарным.

Многоместное отношение используется, например, в теории баз данных.

Пример.: R  A₁  A₂  …  A_n = {(a₁, a₂, … ,a_n) | a₁  A₁ & a₂  A₂ & … a_n  A_n}.

A₁ = A₂ = … = A_n = A

Пусть R₁  A C, аR₂C B. Композицией двух отношений R₁ и R₂ называется отношение R A В, определяемое следующим образом:

R:=R₁ 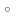R₂:={(а,b) | a  A & b B & c C & aR₁c & cR₂b}

Композиция отношений на множестве А является отношением на множестве А.
Пусть R – отношение на множестве А.

Определение 2.6.Степенью отношения R на множестве А называется его композиция с самим собой. Rⁿ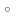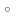:= R … R

Соответственно: R⁰= 1; R¹=R; R² =R 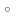Rи вообщеRⁿ=R R^n-1
Если R – отношение из А в В, то есть R  A B.

Определение 2.7. Композиция отношения R R^-1 называется ядром отношения R.

Ядро отношения R из А в В является отношением на множества А.