лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4

• Название: Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
• Анкор: лекции по дм
• Дата: 08.02.2021
• Размер: 1.51 Mb.
• Имя файла: лекции.docx
• Тип: Документы; #174835
• страница: 3 из 40

Свойства теоретико-множественных операций.

Пусть задан универсум U, тогда для любых множеств A, B, C, являющихся подмножеством U выполняются следующие свойства:

1) Идемпотентность:	A  A = A	A  A =A
2) Комутативность:	AB=BA	AB=BA.
3) Ассоциативность:	A(BC) = (AB)C	A(BC)=(AB)C.
4) Дистрибутивность:	A(BC)=(AB)(AC)	A(BC)=(AB)(AC).
5) Поглощение:	(AB)A=A	(AB)A=A.
6) Свойствонуля:	A =A	A =.
7) Свойство единицы:	AU=U	AU=A.
8) Инволютивность:
9) Законы де Моргана:	= 	= .
10) Свойства дополнения:	A = U	A = .
11) Свойство разности:	A \ B = A 

В справедливости этих свойств можно убедиться различными способами, например нарисовать диаграммы Эйлера для левой и правой частей равенства и убедиться, что они совпадают, или же привести формальное рассуждение для каждого равенства.

Представление множеств в ЭВМ

Задать представление какого-либо объекта (в данном случае множества) – значит описать в терминах используемой системы программирования структуру данных, используемую для хранения информации о представляемом объекте, и алгоритмы над выбранными структурами данных, которые реализуют присущие данному объекту операции.

Применительно к множествам определение представления подразумевает описание способа хранения информации о принадлежности элементов множеству и описание алгоритмов для вычисления объединения, пересечения и других введенных операций. Выбор представления зависит от целого ряда факторов: особенностей представляемого объекта, состава и относительной частоты использования операций в конкретной задаче и т.д.

Деревья двоичного поиска – основная структура данных для представления множеств, чьи элементы упорядочены посредством некоторого отношения линейного порядка, которые, как правило, обозначают символом “<”. Эти структуры особенно полезны, когда исходное множество такое большое, что не рационально использовать его элементы непосредственно в качестве индексов массивов. Предполагается, что все элементы множеств являются элементами некоторого универсального множества – универсума, примером которого служит множество возможных идентификаторов в программе на языке Pascal. На деревьях двоичного поиска можно реализовать операторы INSERT, DELETE, MEMBER, и MIN, причём время их выполнения в среднем имеет порядок 0(log n) для множеств, состоящих из n элементов. Дерево двоичного поиска – это двоичное дерево, узлы которого помечены элементами множеств, или, другими словами, узлы дерева содержат или хранят элементы множества.

Реализация операций над подмножествами заданного универсума в ЭВМ.

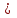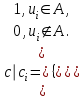Пусть задан конечный универсум U. U={u₁, u₂, …, u_n}, число элементов в нём не превосходит разрядности компьютера. Подмножество A U представлено кодом , где с_i – i-тый разряд кода с.

Тогда код AB – поразрядное логическое произведение кодов А и В.

Код AB – поразрядная логическая сумма кода множества А и кода множества В.

Код - инверсия кода множества А.
Тема 2. Упорядоченные пары. Прямое произведение множеств. Отношения. Многоместные отношения. Композиция отношений. Степень отношений. Ядро отношения. Свойства отношений. Представление отношений в ЭВМ.