лекции по дм. лекции. Основные понятия теории множеств. Способы задания множеств 4 Диаграммы Венна. 4
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Свойства отношений.Пусть R – есть отношение на множестве А: R A А | a , b A Введем следующие понятия: 1) обратное отношение: R-1:={(a,b)|(b,a)R}; 2) дополнение отношения: := {(a,b)|(a,b) R }; 3) тождественное отношение: I:= {(a,a)|a R}; 4) универсальное отношение: U:= {(a,b) |aA&bA}. Замечание: пусть R – отношение на множестве А (R А2), тогда: Если аА, аRа, то отношение R называется рефлексивным. Если аА, ¬аRа, то такое отношение R называют антирефлексивным. Если а,bА, аRbbRа. Такое отношение R называют симметричным. Если а,bА, аRb&bRа a=b. Такое отношение R называют антисимметричным. Если а,b,сА, аRb&bRс аRс. Такое отношение R называют транзитивным. Если а,bА, аbaRb bRa. Такое отношение R называют полным (линейным). Теорема: пусть R – отношение на множестве А, то есть RAА, тогда: отношение R рефлексивно тогда и только тогда, если тождественное отношение включается во множество R. отношение R симметрично тогда и только тогда, когда R = R-1 (равно обратному отношению). отношение R транзитивно тогда и только тогда, когда композиция отношений R·RR (включается в отношение R). отношение R антисимметрично тогда и только тогда, когда пересечение отношения R с обратным отношением включается в тождественное отношение: RR-1I. отношение R антирефлексивно тогда и только тогда, когда пересечение отношения R с тождественным отношением I образует пустое множество: R I= . отношение R полно тогда и только тогда, когда объединение отношения R с тождественным отношением I и с обратным отношением образует полное отношение U: R I R-1 = U. Для операции композиции отношений существуют две теоремы, позволяющие оценить результат: R1 R2 R1 R2 R1 R2 R1 R2 Теорема:    = =   | ( | (   )[i, j]:= )[i, j]:= 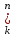  [i, k]& [i, k]& [k, j] [k, j]R1 R2 R1 R2 R1 R2 Теорема:  = =  | ( | (  )[i, j]:=R1 [i, j] R2 [i, j] )[i, j]:=R1 [i, j] R2 [i, j]Пример Пусть есть множества А и В, на которых заданы отношения δ и ρ соответственно, и  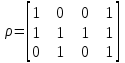 , то композиция отношений , то композиция отношений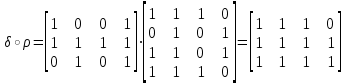 |
