Основные пути снижения издержек при транспортировке материально-технических ресурсов. Основные пути снижения издержек при транспортировке материально-. Основные пути снижения издержек при транспортировке материальнотехнических ресурсов

Название	Основные пути снижения издержек при транспортировке материальнотехнических ресурсов
Анкор	Основные пути снижения издержек при транспортировке материально-технических ресурсов
Дата	28.04.2022
Размер	461 Kb.
Формат файла
Имя файла	Основные пути снижения издержек при транспортировке материально-.doc
Тип	Курсовая #502518
страница	5 из 5

1 2 3 4 5

Глава 5. Задача о назначениях.

Третья задача – оптимизация движения сквозного материального потока направлена на сокращение времени выполнения объёма перевозок, т.е. сокращение времени выполнения заказов при максимальной производительности транспортных средств.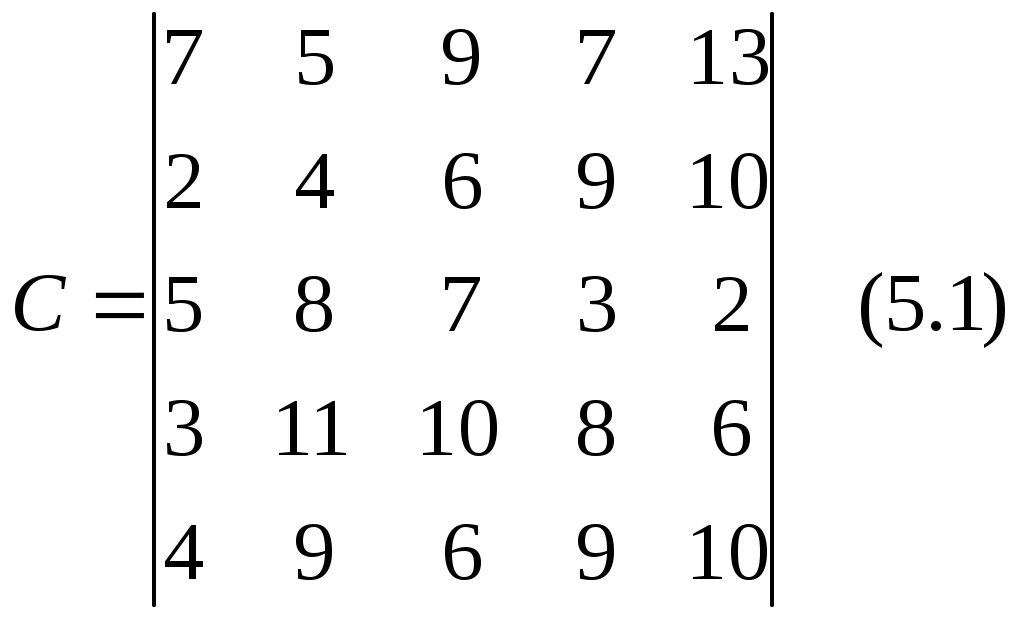

Воспользуемся венгерским методом решения задач.

Имеется 5 поставщиков и 5 пунктов потребления. Матрица затрат времени i-той машины и j-ому потребителю имеет вид (5.1).

Шаг 1. Т.к. задача о назначении формулируется, как задача максимизации, то сводим её к задаче на минимум следующим образом: в матрице эффективности С находим максимальный элемент d=max c_ij и строим матрицу D=||d_ij|| по следующему правилу: d_ij=d-c_ij; i,j=

(5.2). В нашем случае d=max c_ij=13. Пользуясь правилом (5.2) строим матрицу D:

Шаг 2. От полученной матрицы D переходим к приведенной матрице D’. Матрица D’ называется приведенной, если она получена из данной матрицы D путем следующих преобразований:

В каждой строке находим минимальный элемент и вычитаем его из всех элементов соответствующей строки. Получаем D’: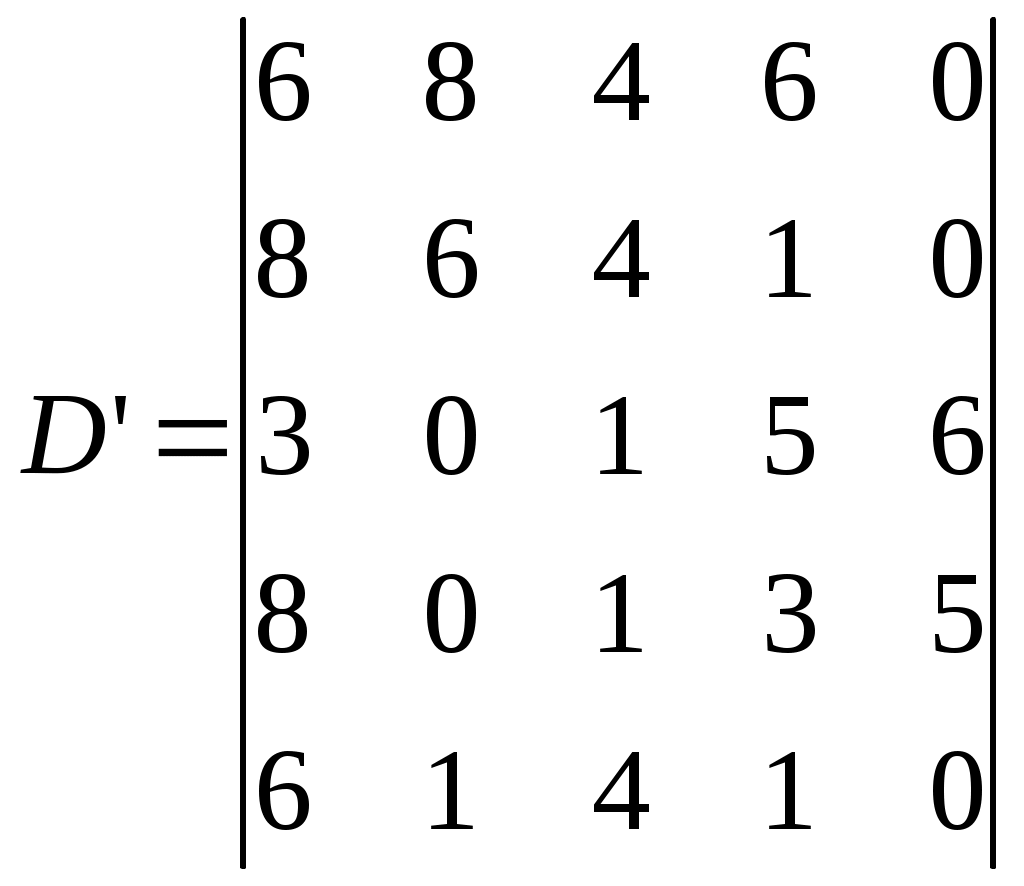

В каждом столбце находим минимальный элемент и вычитаем его из элементов соответствующего столбца. Получим D":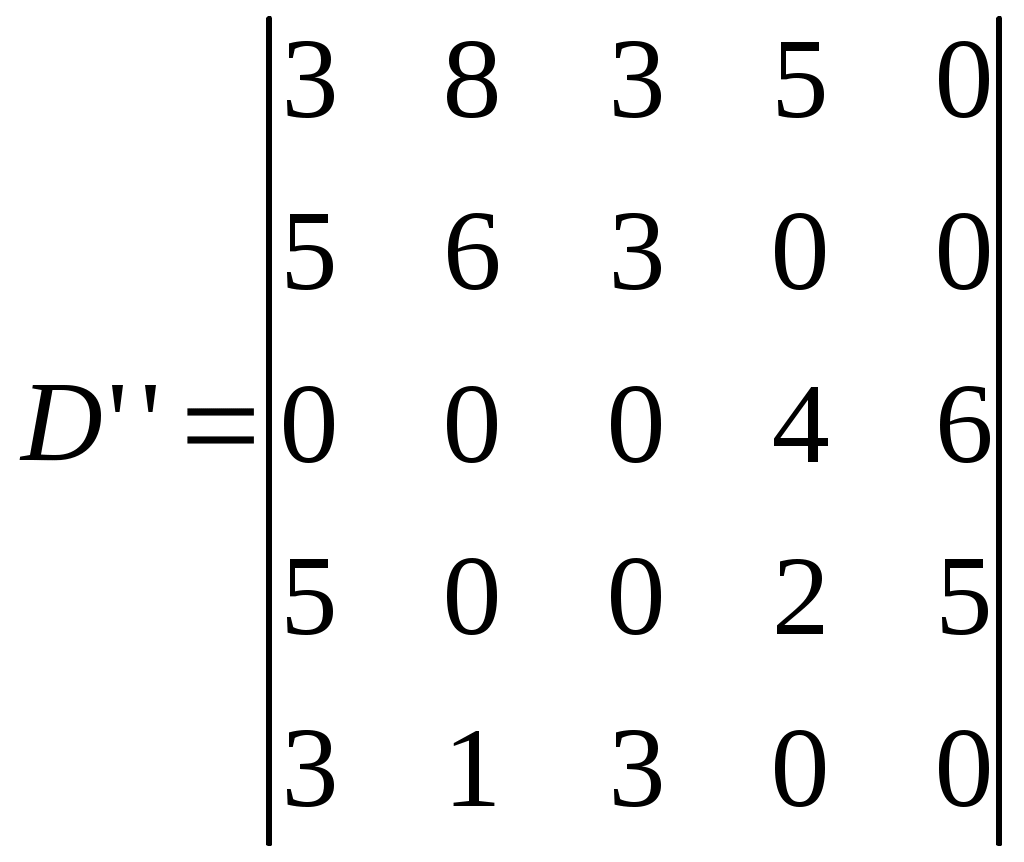

Ш аг 3. В приведенной матрице D" выбираем строку, имеющую наименьшее число нулей. В этой строке выбираем один из нулей и отмечаем его (*), а остальные нули строки и столбца зачеркиваем. Эту процедуру проводим последовательно для всех строк.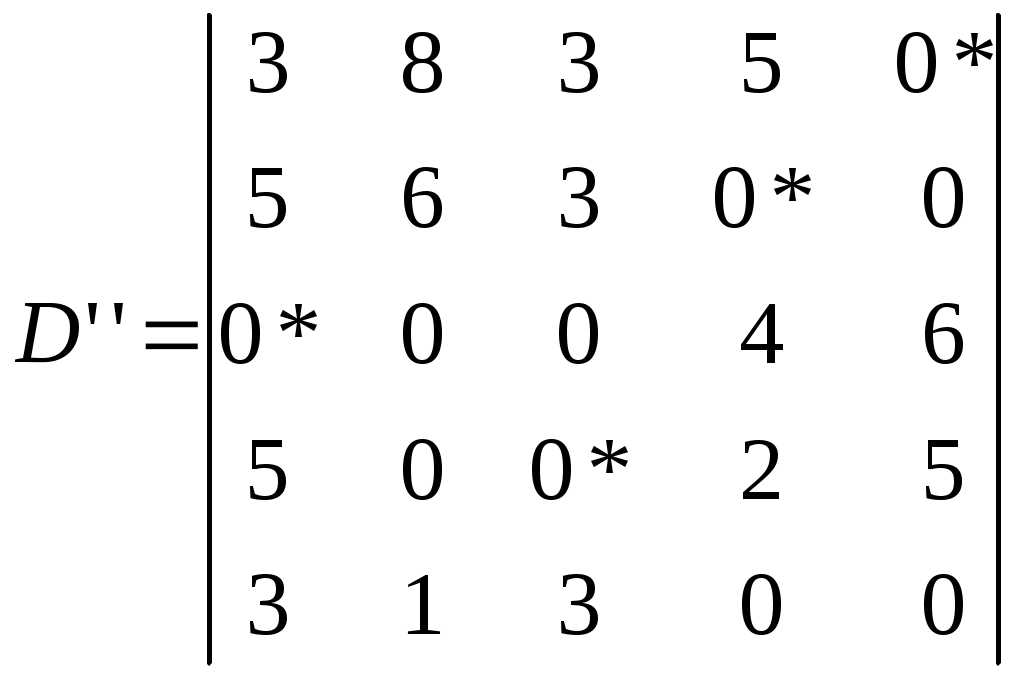

Шаг 4. В оставшейся, состоящей из незачеркнутых элементов матрице находим минимальное значение элемента (в нашем случае min x=1). Прибавляем его (min x=1) к элементам матрицы, стоящим на пересечении зачеркнутого столбца и строки и вычитаем из всех незачеркнутых элементов.

Получим следующую модифицированную матрицу: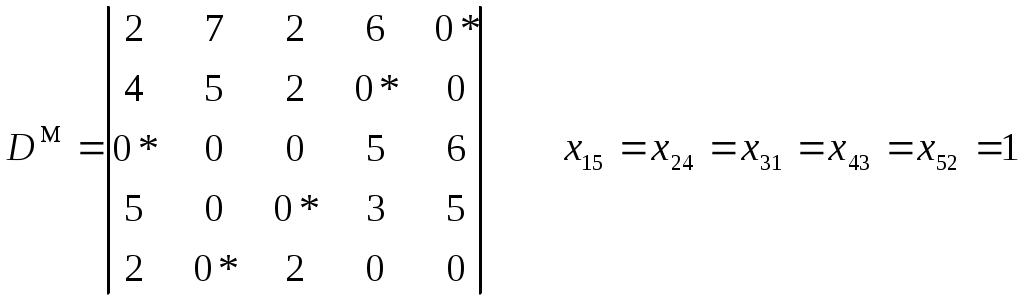

Суммарное время выполнения заказа на перевозку равно:

t_min(D)=d₁₅+d₂₄+d₃₁+d₄₃+d₅₂=0+4+8+3+4=19;

Суммарная максимальная производительность труда равна:

t_max(C)=c₁₅+c₂₄+c₃₁+c₄₃+c₅₂=13+9+5+10+9=46.

Следовательно, время выполнения заказа получилось равным 19 часам, а производительность труда стала равной 46 т.

Итак, решив три задачи по логистической оптимизации материального потока получилась дополнительная прибыль только за счёт рационального управления материальным потоком, без дополнительных капитальных вложений.

Заключение

Сбытовая функция в сфере логистики осуществляется посредством выполнения 6 условий: груз, качество, количество, время, затраты, пункт назначения. Это говорит нам о том, что мы имеем дело с управлением материальным потоком и связанным с ним потоком информации от ввода в систему до конечной продажи. Если рассматривать поставленную задачу с позиции критерия логистической системы “точно в срок”, то можно с уверенностью сказать, что мы ориентированы на удовлетворение потребностей потребителя, т.е. учитываем его запросы, ряд специальных условий, наличие продукции на рынке при заранее определенных затратах и параметрах обслуживания.

Решая транспортные проблемы, необходимо использовать теоретические и методологические достижения в этой области. Однако важно применять не только имеющиеся достижения, но и выработать свою транспортную стратегию и определить главные ее принципы. В основе логистической модели должны лежать проблемы транспортного процесса, которые бы включали в эту модель реалистические предположения. Важной областью исследований является разработка аналитических результатов для распределения эвристики маршрутизации транспортных средств, изучение компромиссов между запасами ресурсов, их транспортировкой и размещением. Отсюда видно, что перспективным направлением исследований может послужить объединение экспертной системы с транспортно-маршрутной системой на основе взаимосвязанной оптимизации.

К предложениям нужно так же отнести компьютеризацию различных звеньев логистической системы, подключение их к единой информационной сети (обладающей высокой скоростью передачи данных и позволяющей эффективно работать с удаленными терминалами), что позволит отслеживать движение груза и контролировать транспортные потоки. Все эти меры призваны снизить величину транспортных расходов и доставить груз точно в срок. С уверенностью можно сказать, что рассмотренное в этой работе направление логистики позволяет снизить величину затрат на содержание запасов и транспортировку продукции к ее получателю при грамотном управлении материалопотоком и потоком продукции от источника до потребителя. Задача об оптимальном назначении позволяет назначить каждого поставщика на один и только один пункт потребителя так, чтобы суммарные затраты были минимальными.

Список использованных источников

Васильев Г.А. и др. «Логистика». – М.: Экономическое образование, 1993.
Гаджинский А.М. Логистика: Учебник для высших и средних специальных учебных заведений. – М.: Информационно-внедренческий центр «Маркетинг», 2000.
Гаджинский А.М. Основы логистики: Учебное пособие. – М.: ИВЦ Маркетинг, 1996.
Залманова М.Е. Закупочная и распределительная логистика. – Саратов: СПИ, 1992.
Курбатова Т.Я., Лебедев К.А. Курс лекций по предмету “Логистика”, 1997.
Логистика: Учебное пособие / Под ред.Б.А.Аникина. – М.: ИНФРА-М, 1999. – 327 с.
Неруш Е.М. Коммерческая логистика. — М.: Банки и биржи, ЮНИТИ, 1997.
Плоткин Б.К. Основы логистики. — Ленинград, 1993
Смехов А.А. Введение в логистику. – М.: Транспорт, 1993.
конспект лекций