Лабортаронаяа_10. Отчет по лабораторнопрактической работе 6 Исследование линейнополяризованного света
 Скачать 65.73 Kb. Скачать 65.73 Kb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Оценка лабораторно-практического занятия | |||||
| Выполнение ИДЗ | Подготовка к лабораторной работе | Отчет по лабораторной работе | Коллоквиум | | Комплексная оценка |
| | | | | | |
Выполнено “____” ___________
Подпись преподавателя __________
Лабораторная работа № 6
Исследование линейно-поляризованного света
Цель работы: проверка закона Малюса и определение степени поляризации света.
Общие сведения
В электромагнитной волне, распространяющейся в безграничном пространстве, векторы напряжённости электрического Е и магнитного Н полей перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны, определяемому волновым вектором k, т. е. электромагнитная волна является поперечной. Плоскость, в которой лежат векторы Е и k, называется плоскостью колебаний, а перпендикулярная ей плоскость, в которой лежат векторы Н и k, – плоскостью поляризации. Если положение плоскости колебаний неизменно во времени, то волна называется плоско- или линейно-поляризованной. Возможны и другие, более сложные типы поляризации поперечной волны, при которых колебания вектора Е, оставаясь в плоскости, перпендикулярной направлению распространения, имеют более сложный характер (конец вектора описывает эллипс или окружность). Волна имеет тогда эллиптическую или круговую поляризацию. Световые волны суть электромагнитные волны с длинами волн от 400 до 760 нм. Свет от обычных (не лазерных) источников (например, нити накаливания ламп) представляет собой совокупность большого числа так называемых волновых пакетов (цугов волн), каждый из которых является результатом единичного акта испускания электромагнитного излучения атомом вещества. Электромагнитная волна в каждом волновом пакете линейно поляризована. Отсутствие взаимосвязи между актами испускания различных атомов приводит к тому, что плоскости колебаний различных волновых пакетов ориентированы случайным образом. Такой распространяющийся от источника свет называется естественным. В естественном свете все ориентации взаимно перпендикулярных векторов Е и Н в плоскости, перпендикулярной направлению распространения волны, равновероятны и плоскость поляризации меняется хаотически. Если положение плоскости колебаний в световой волне каким-либо образом упорядочено, то свет поляризован (частично поляризован).
Получение поляризованного света возможно при разнообразных физических эффектах – прохождения света через анизотропные среды, отражении от диэлектриков и др. Устройства для получения поляризованного света называются поляризаторами. Поляризаторы пропускают колебания, параллельные плоскости, называемой плоскостью поляризатора, и полностью или частично задерживают колебания, перпендикулярные этой плоскости.
Поляризация при двойном лучепреломлении. Если электромагнитная волна падает на границу раздела двух изотропных сред, то во второй среде имеется только одна волна, распространяющаяся по «обычным» законам преломления. Если вторая среда анизотропна, т. е. её свойства (в частности диэлектрическая проницаемость) различны вдоль разных направлений, то во второй среде распространяются две различно преломлённых волны (обыкновенная и необыкновенная) с разными скоростями. Это явление называется двойным лучепреломлением. Обыкновенная и необыкновенная волны линейно поляризованы, и плоскости их колебаний взаимно перпендикулярны. Эффект двойного лучепреломления света наблюдается в прозрачных анизотропных кристаллах. У одноосных кристаллов (исландский шпат, турмалин) имеется направление (оптическая ось), вдоль которого обе волны распространяются с одинаковой скоростью. Плоскость, проведённая через оптическую ось кристалла и направление распространения света, называется главным сечением кристалла. Колебания вектора Е в обыкновенной волне перпендикулярны плоскости главного сечения кристалла, в необыкновенной – совершаются в плоскости главного сечения.
Одним из широко распространённых поляризаторов света является призма Николя (рис. 6.1), изготовленная специальным образом из исландского шпата так, что необыкновенная e волна проходит через призму, а обыкновенная о претерпевает на прослойке AA′ из канадского бальзама полное отражение и поглощается зачернённой гранью A′C.
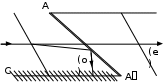 |
| Рис. 6.1. Поляризатор (призма) Николя |
Закон Малюса. Пусть на поляризатор падает плоскополяризованная волна с амплитудой напряжённости электрического поля Е1, плоскость колебаний которой (волны) образует с плоскостью главного сечения поляризатора угол (рис. 6.2). Интенсивность падающей волны пропорциональна квадрату напряжённости электрического поля I1E12. В световой волне на выходе поляризатора амплитуда напряжённости электрического поля будет равна Е1 cos , а интенсивность света, соответственно, пропорциональна (Е1 cos )2.
Таким образом,
I= I1 cos2 . (6.1)
Соотношение (6.1) отображает закон Малюса.
| Рис. 6.2. К обоснованию закона Малюса |

сли на поляризатор падает естественный свет с интенсивностью I0, то все значения φ равновероятны, и доля света, прошедшего через поляризатор, будет равна среднему значению cos2 φ, т. е. 1/2. При вращении поляризатора вокруг направления естественного луча интенсивность прошедшего света остаётся постоянной, а изменяется лишь ориентация плоскости колебаний света, выходящего из прибора. Интенсивность прошедшего света, регистрируемая детектором, при этом остаётся постоянной и равной I0/2. Если после первого поляризатора установить второй однотипный поляризатор, называемый анализатором, то интенсивность I2 на выходе анализатора будет изменяться по закону Малюса (6.1):
I2 = I1cos2 = (I0/2) cos2 ,
где I0 и I1 – интенсивности естественного и линейно-поляризованного света на входе первого и второго поляризаторов соответственно; φ – угол между плоскостями поляризатора и анализатора.
Частично поляризованный свет. Степень поляризации. Идеальных поляризационных устройств не бывает, и полученные с помощью реальных поляризационных устройств световые пучки всегда частично поляризованы, т. е. представляют собой смесь поляризованного и неполяризованного света с интенсивностями Iпол и Iест. Для характеристики частично поляризованных световых пучков вводят понятие степени поляризации, под которой понимают отношение интенсивности поляризованной составляющей к полной интенсивности светового пучка:
P= Iпол /( Iпол + Iест).
Этому выражению можно придать другой вид. Если такой частично поляризованный свет пропустить через анализатор, то при вращении прибора вокруг направления луча интенсивность света на его выходе будет изменяться в пределах от Imax = Iпол + Iест /2 до Imin = Iест /2 при параллельных и взаимно перпендикулярных плоскостях поляризатора и анализатора соответственно. При этом учтён тот факт, что естественная составляющая ослабляется при прохождении через анализатор в два раза, а поляризованная – в соответствии с законом Малюса. Выразив Iпол и Iест через Imax и Imin, получим другое выражение для степени поляризации:
P = (Imax Imin)/(Imax + Imin). (6.2)
Для плоскополяризованного света Imin = 0 и Р = 1.
Экспериментальная установка (рис. 6.3) состоит из источника естественного света S (лампа накаливания), диафрагмы D, линзы L, сменных светофильтров С, поляризатора Р, анализатора А, фотоэлемента Ф и микроамперметра РА. Угол между главными сечениями поляризатора и анализатора можно изменять вращением анализатора вокруг оси, совпадающей с оптической осью установки. Угловое положение главного сечения анализатора определяется по шкале, находящейся на его оправе.

Рис. 6.3. Установка для анализа частично поляризованного света
Сила тока в цепи фотоэлемента пропорциональна интенсивности света I, падающего на фотоэлемент. Интенсивность света, прошедшего через анализатор, измеряется в условных единицах (делениях шкалы микроамперметра).
Указания по проведению эксперимента
1. Включить лампу S. Переключатель светофильтров установить в положение без светофильтра. Поворачивая анализатор, найти положения, соответствующие максимальному и минимальному показаниям микроамперметра. Записать значения углов max и min по шкале анализатора и показания микроамперметра Imax и Imin (в делениях шкалы).
2. Изменяя угол от 0 до 360º с шагом в 10º, регистрировать показания микроамперметра и результаты наблюдений заносить в табл. 6.1 с учётом Imax, Imin и max, min.
3. На пути светового пучка установить один из светофильтров. Поворачивая анализатор, наблюдать показания I микроамперметра. Занести в табл. 6.2 максимальное Imax и минимальное Imin показания микроамперметра (в делениях шкалы). Повторить наблюдения 5 раз.
4. Последовательно заменяя светофильтры, повторить наблюдения п. 3.
Таблица 6.1
Проверка закона Малюса
| , …º | 0 | 10 | 20 | | 360 |
| I, дел. | | | | | |
| I/Imax (эксперимент) | | | | | |
| max, …º | | | | | |
| сos2 I/Imax (теория) | | | | | |
Таблица 6.2
Определение степени поляризации света
| Светофильтр. Длина волны, нм | № измерения | Imax | Imin | Imax Imax | Imin Imin | P P |
| 1. < 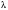 < < | 1 | | | | | |
 | | | ||||
| 5 | | | ||||
 | 1 | | | | | |
 | | | ||||
| 5 | | | ||||
| 4. < 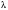 < < | 1 | | | | | |
 | | | ||||
| 5 | | |
5. Выключить лампу. Записать значение «темнового» тока фотоэлемента в делениях шкалы микроамперметра. Исключить эту систематическую погрешность из данных табл. 6.2.
Указания по обработке результатов
1. Поскольку максимальная интенсивность света на выходе анализатора наблюдается при совпадении главных сечений поляризатора и анализатора (т. е. при = 0), определить углы = max. Результаты представить в табл. 6.1.
2. Рассчитать экспериментальную зависимость I/Imax угла и теоретическую по формуле (6.1), данные записать в табл. 6.1. Построить график зависимости (I/Imax)теор = f1(), на этом же графике нанести экспериментальные точки (I/Imax)эксп = f2().
3. Сравнить расчётные и экспериментальные данные, дать заключение о справедливости закона Малюса в исследованной ситуации.
4. Для каждого из светофильтров вычислить средние значения Imax, Imin и доверительные интервалы Imax, Imin. Результаты представить в табл. 6.2.
5. Считая анализатор идеальным, определить исходя из (6.2) степень поляризации света, прошедшего через поляризатор, для исследованных участков спектра:
P Imax IminImax Imin.
6. Вывести формулу для доверительного интервала Р и вычислить Р для исследованных участков спектра.
7. Представить результаты измерения степени поляризации света в табл. 6.2 в стандартной форме.
Контрольные вопросы
1. В чём отличие естественного света от поляризованного?
2. Какой свет называется плоскополяризованным? Поляризованным по кругу; по эллипсу?
3. В чём отличие плоскополяризованного от частично поляризованного света?
4. Что называют степенью поляризации света? Как она определяется?
5. Каково назначение поляризатора и анализатора?
6. Дайте определение понятию «главное сечение поляризатора».
7. Разъясните принцип действия поляроида.
8. Будет ли выполняться закон Малюса при прохождении через анализатор частично поляризованного света?
Протокол наблюдений к лабораторной работе №6
| º | I, дел. | I/Imax (эксперимент) | max | сos2 I/Imax (теория) | º | I, дел. | I/Imax (эксперимент) | max | сos2 I/Imax (теория) |
| 0 | | | | | 190 | | | | |
| 10 | | | | | 200 | | | | |
| 20 | | | | | 210 | | | | |
| 30 | | | | | 220 | | | | |
| 40 | | | | | 230 | | | | |
| 50 | | | | | 240 | | | | |
| 60 | | | | | 250 | | | | |
| 70 | | | | | 260 | | | | |
| 80 | | | | | 270 | | | | |
| 90 | | | | | 280 | | | | |
| 100 | | | | | 290 | | | | |
| 110 | | | | | 300 | | | | |
| 120 | | | | | 310 | | | | |
| 130 | | | | | 320 | | | | |
| 140 | | | | | 330 | | | | |
| 150 | | | | | 340 | | | | |
| 160 | | | | | 350 | | | | |
| 170 | | | | | 360 | | | | |
| 180 | | | | | | ||||
βmax = Imax = мкА
βmin = Imin = мкА
βmax =
βmin =
| Светофильтр. Длина волны, нм | № измерения | Imax | Imin | Imax Imax | Imin Imin | P P |
| 1. 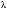 685 685 | 1 | | | | | |
| 2 | | | ||||
| 3 | | | ||||
| 4 | | | ||||
| 5 | | | ||||
| 2. 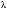 626 626 | 1 | | | | | |
| 2 | | | ||||
| 3 | | | ||||
| 4 | | | ||||
| 5 | | | ||||
| 3. 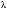 580 580 | 1 | | | | | |
| 2 | | | ||||
| 3 | | | ||||
| 4 | | | ||||
| 5 | | | ||||
| 4. 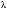 437 437 | 1 | | | | | |
| 2 | | | ||||
| 3 | | | ||||
| 4 | | | ||||
| 5 | | | ||||
| 5. 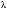 408 408 | 1 | | | | | |
| 2 | | | ||||
| 3 | | | ||||
| 4 | | | ||||
| 5 | | |
∆I = мкА
ΘI = мкА
Iтемн = мкА
