Построить принципиальную схему 2-х позиционного 4-х канального диффе-ренциального пневмораспределителя с односторонним гидравлич. Отчет по лабораторной работе 1 Исследование типовых структурных звеньев

Название	Отчет по лабораторной работе 1 Исследование типовых структурных звеньев
Анкор	Построить принципиальную схему 2-х позиционного 4-х канального диффе-ренциального пневмораспределителя с односторонним гидравлич
Дата	03.11.2021
Размер	165.1 Kb.
Формат файла
Имя файла	Lab_rab_1_Derevyanko.docx
Тип	Отчет #262077
страница	2 из 2

1 2

Колебательное звено.

Типовое колебательное звено описывается дифференциальным уравнением второго порядка

((Т₁р)² + Т₂р + l)y(t) = kx(t),

где Т1,Т2 - постоянные времени колебательного звена, к - коэффициент усиления звена.

Передаточная функция колебательного звена

W(P) =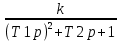

Таблица 8 - Исходные данные для построения АФЧХ колебательного звена

Вариант	1	2	3	4	5	6
к	10	10	10	15	15	15
Т1	1.0	1.0	0.1	0.1	1.0	1.0
Т2	1.0	0.5	1	1	0.8	1.0

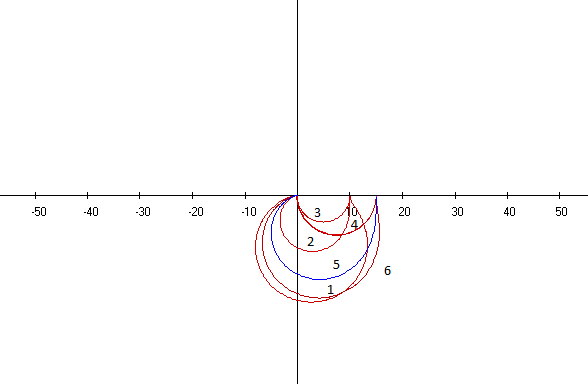Рисунок 4- АФЧХ для Колебательного звена -чем больше коэффициент к, тем больше значение амплитуды -значение амплитуды зависит от коэффициента демпфирования. ( ɛ = T₂/2Ti). Чем больше значение коэффициента, тем меньше амплитуда, и наоборот.

-Чем больше коэффициент демпфирование, тем более правильной формы петля.

-Чем меньше Т\ (при неизменном Т) Таблица 10

	ω=1/ T₁	Фаз.сдвиг	ω=2/ T₁	Фаз.сдвиг	§=Т₂/2 T₁
1	1	-90°	2	-146,3°	0,5
2	1		2	-161,6°	0,25
3	10		20	-98,5°	5
4	10		20	-98,5°	5
5	1		2	-151,9°	0,4
6	1		2	-146,3°	0,5

П
1. k_max=l 1.5 при w=0.7
2. k_max=20.5 при w=0.9
3. k_max=10.0 при w=0.0
4. k_max= 15.0 при w=0.0
5. k_max=20.4 при w=0.8
6. k_max=15.0 при w=0.
ри w=2/ T₁=2, А=2.8, (р=-146.3°
При w=2/ T₁=2, А=3.2, ф=-161.6°
При w=2/ T₁₌20, А=0.5, (р=-98.5°
При w=2/ T₁=20, А=0.7, φ=-98.5°
При w=2/ T₁=2, А=4.4, φ=-151.9°
П
1. ɛ =5
2. ɛ =0.4
3. ɛ =0.5
ри w=2/T₁=2, А=4.2, (р—146.3° в = Т₂/2Т

ɛ-0.5
ɛ =0.25
ɛ =5

Таблица 11 - Исходные данные для построения ЛАХ колебательного звена

Вариант	1	2	3	4	5	6	7	8	9
k	15	15	15	15	15	15	10	10	10
T1	1	0.001	0.001	0.001	0.001	0.001	0.1	0.1	0.1
T2	1	0.001	0.0001	0.0005	0.0008	0.002	0.1	0.01	1

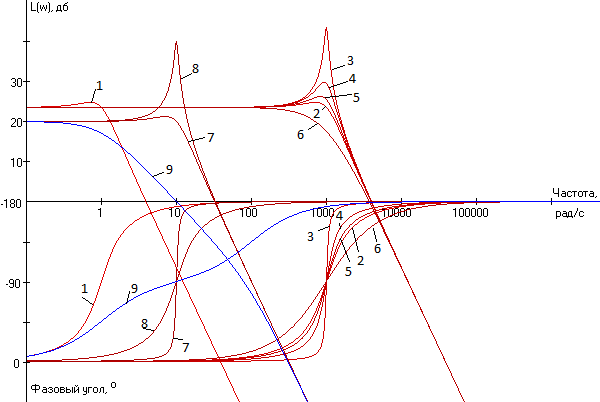Рисунок 5 -ЛАХ для колебательного звена

1. 1) L(w)= 24.8, w= 0.7, φ =-53.0

L(w)= 24.8, w=691.8, φ =-53.0
L(w)= 43.5, w=1000, φ =-90.0
L(w)= 29.8, w= 940.4, φ =-76.2
L(w)= 26.2, w=806.6, φ =-61.6
L(w)= 23.5, w=0.1, φ =-0.0
L(w)= 21.2, w= 7.1, φ =-55.5
L(w)= 40.0, w= 10.0, φ =-90.0
L(w)= 20.0, w=0.1, φ =-5.7

2. 1) При w=l/T]=l, k=14.96, φ =-90°

При w=l/T₁=1000₅ к=14.96, φ =-90°
При w= 1 / T₁=1000, к=149,62, φ=-90°
При w=l/ T₁=1000, к=29.85, φ=-90°
При w= 1 / T₁=1000, к= 18.83, φ =-90°
При w=l/ T₁=1000, к=7.49, ф=-90°
При w=l/ T₁=10, к=10, φ =-90°
При w=l/ T₁^:=10, к=104.71, φ =-90°
При w=l/ T₁=10, к , φ =-90°

1) При w=2/T₁=2, к=4.31, φ =-145.5°

При w=2/ T₁=2000, к=4.31, φ =-145.5°
При w=2/ T₁=2000, к=5.24, φ =-176.1°
При w=2/T₁=2000, к=4.95, φ =-161.0°
При w=2/ T₁=2000, к=4.57, φ =-151.2°
При w=2/ T₁=2000, к=3.09, φ —126.1⁰
При w=2/ T₁=20, к=2.69, φ =-146.9°
При w=2/ T₁=20, к=3.5, φ =-176.1°
При w=2/ T₁=20, к=0.5, φ =-98.3°

1) w_c =3.7, φ =-164.0°

w_c=3744, φ =-164.0°
w_c=3744 ,φ =-178.4°
w_c=3744, φ =-171.8°
w_c=3744, φ =-167.0°
w_c=3521, φ =-148.3°
w_c =30.2, φ =-159.6°
w_c=31 Л, φ =-177.9°
w_c=8.8 , φ =-88.6°

1) w=3414, φ =-178.2°

w=31141, φ =-178.2°
w=3414, φ =-178.2°
w=T5848, φ =-178.2°
w=25118, φ =-178.2°
w=63095, φ =-178.2°
w=331.1, φ =-178.2°
w=35.2, φ =-178.2°
w=3114, φ =-178.2°

Коэффициент усиления звена к определяет начальное значение амплитуды L(w).
Постоянные времени связаны между собой коэффициентом демпфирования 8⁼Т₂/2Т 1. Чем меньше значения Т1 и Т2, тем дольше держится неизменным знамение амплитуды L(w).

-Чем больше значение е, тем плавнее переход графика, чем меньше значение 8, тем больше скачок и тем круче переход угла от 0 до -180.

Таблица 12-Исходные данные для построения переходных характеристик колебательного звена

Вариант	1	2	3	4	5	6
к	10	10	10	10	15	15
Т1	0.2	0.2	0.2	0.2	0.5	0.2
Т2	0.2	0.1	0.05	1	0.5	0.2

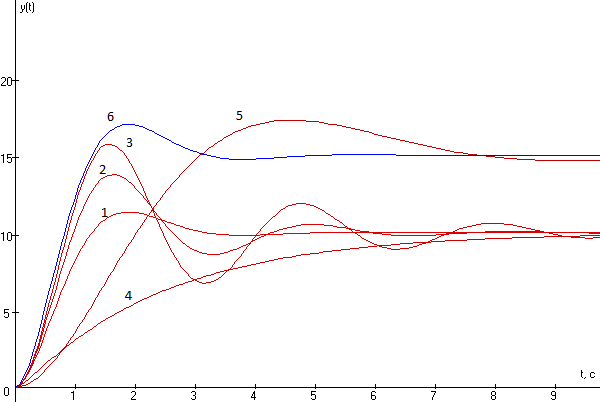Рисунок 6-Переходные характеристики для колебательного звена

- Чем меньше значения Т1 и Т2, тем быстрее, сигнал доходит до своего установившегося значения.

-Чем меньше коэффициент демпфирования г, тем больше колебаний будет происходить, и тем дольше будет устанавливаться значение сигнала У_уст.

S=0.132 4) S- нет
S=0.374 5) S=0.15
S=0.572 6) S-0.132

Интегрирующее звено.

Интегрирующее звено ликвидирует статические ошибки.

Тp -y(t) = к * x(t)

Таблица 13-Исходные данные для построения переходных характеристик интегрирующего звена

Вариант	1	9	3	4	5
к	10	10	10	10	15
Т	0.5	1	2	3	2

- чем больше величина постоянной времени Т, тем меньше угол наклона кривой к оси времени.

-чем больше коэффициент к, тем больше угол наклона кривой к оси времени.

Вариант	1	2	3	4	5
к	10	10	10	10	15
Т	0.5	1	2	3	2
t	1.21	2.47	4.97	7.43	4.98

4. Дифференциальное звено

(

Рисунок 7- Переходные характеристики для интегрирующего звена Таблица 14

Tр + 1 )y(t) = Tpx(t) где к - коэффициент преобразования звена,

x(t), y(t) - функции входного и выходного сигналов звена, р - оператор дифференцирования.

Таблица 15-Исходные данные для построения переходных характеристик дифференциального звена

Вариант	1	2	3	4
Т1	0.1	0.5	1	2

-чем больше постоянная времени Т, тем меньше начальное значение выходного сигнала.

Рисунок 8- Переходные характеристики для дифференциального звена

При t = 0 график производной ступенчатой функции стремиться к бесконечности, а график реального дифференциального звена принимает конкретное значение.

Вывод:

В ходе выполнения лабораторной работы были изучены частотные характеристики типовых структурных звеньев и взаимосвязи между видом частотных характеристик и переходными процессами в звеньях.

1 2