Отчет по лабораторной работе 1 Многокритериальная оптимизация технологических процессов
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
|
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего образования «Уфимский государственный авиационный технический университет» Кафедра СиМ Отчет по лабораторной работе №1 «Многокритериальная оптимизация технологических процессов» Вариант №8 Выполнили: студенты группы СМ-217 Манапова А.Н. Сулейманова З.Ю. Проверил: старший преподаватель Сафина А.Ф. Уфа, 2018 г. СодержаниеЦель работы 3 Основные теоретические сведения 3 Задание 5 Условие 6 Ход работы 7 Однокритериальная оптимизация 7 Многокритериальная оптимизация 9 Выводы 11 Цель работы Целью лабораторной работы является ознакомление с методами оптимизации процессов и получение практических навыков проведения оптимизации технологических процессов на различных иерархических уровнях по различным критериям. Основные теоретические сведения Технологический процесс является иерархической системой с детерминированной структурой. Не представляет трудностей исследование структуры, т.к. она является искусственно созданной. Технологический процесс разделяется на этапы, операции, технологические переходы, установы, ходы. В пределах рассматриваемого иерархического уровня элементы этого уровня связаны друг с другом, что может быть отражено в виде соответствующего сетевого графа. Нас в основном интересует уровень операций, поскольку операция является основным структурным элементом технологического процесса. Граф, отображающий последовательность выполнения операций техпроцесса, является, как правило, многовариантным. Основной целью системного анализа технологического процесса на операционном уровне является выбор оптимального маршрута: такого пути на многовариантном графе, который является наилучшим по выбранным заранее критериям. Рассмотрим подробнее процесс выбора оптимального пути (варианта технологического процесса). Основными критериями оптимизации могут быть: приведенные затраты на операцию, штучное (штучно-калькуляционное) время и др. В качестве дополнительных критериев оптимизации могут служить площадь, занимаемая оборудованием, энергоемкость и др. Существует ряд методов решения многокритериальных оптимизационных задач, наиболее используемыми являются: - построение обобщенного критерия оптимизации; - пороговая оптимизация. Оптимизация по обобщенному критерию Суть данной процедуры сводится к следующему: вершинам графа (i=1,n) (которые обозначают технологические операции) при нормировании ставится в соответствие величина обобщенного критерия оптимизации, который определяется по формуле: 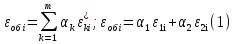 где 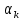 – весовой коэффициент, определяющий значение k -го критерия и назначаемый экспертно; – весовой коэффициент, определяющий значение k -го критерия и назначаемый экспертно; 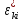 - значение k -го критерия для i-й вершины графа, приведенного к относительному виду. - значение k -го критерия для i-й вершины графа, приведенного к относительному виду.Причем, должно выполняться условие: 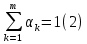 Величина 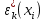 определяется по формуле: определяется по формуле: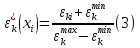 где 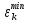 , , 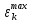 - соответственно минимальное и максимальное значения, которое принимает k-й критерий оптимизации на всех n вершинах графа. - соответственно минимальное и максимальное значения, которое принимает k-й критерий оптимизации на всех n вершинах графа. Из зависимости (3) видно, что 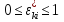 К примеру, если каждой i-й вершине графа приписаны три критверия оптимизации - себестоимость обработки 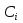 , штучное время , штучное время 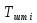 , площадь под оборудованием , площадь под оборудованием 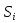 , то зависимость (1) в этом случае будет иметь вид: , то зависимость (1) в этом случае будет иметь вид: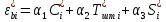 Весовые коэффициенты 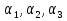 назначаются исходя из важности того или иного критерия с учетом соотношения (2). назначаются исходя из важности того или иного критерия с учетом соотношения (2).Пороговая оптимизация На множестве всех возможных путей графа q, соединяющих первую вершину с последней, определим понятие j-й длины пути (j=1,q) по k-му критерию оптимизации 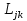 : это сумма значений k-го критерия по всем вершинам j-го пути. : это сумма значений k-го критерия по всем вершинам j-го пути.Пороговая оптимизация выполняется в виде следующих шагов. 1) Назначают главный 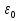 и множество второстепенных критериев оптимизации и множество второстепенных критериев оптимизации 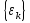 , k=1,m-1 и присваивают их каждой вершине графа (операции): , k=1,m-1 и присваивают их каждой вершине графа (операции): 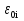 , , 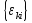 , k=1,m-1. , k=1,m-1.2) Определяем множество 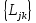 , j=1,q, k=1,m с помощью программы AMACONT, выбрав в качестве основного критерия – критерий , j=1,q, k=1,m с помощью программы AMACONT, выбрав в качестве основного критерия – критерий 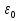 . . В результате получается полный перечень путей графа, отсортированный в порядке возрастания основного критерия 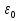 . .3) Для каждого k-го второстепенного критерия экспертно назначается ограничение (порог) на длину пути 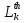 . .Пороговое значение 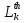 отсекает часть множества q всех путей графа: путь отсекается – вычеркивается из перечня, полученного в п.2, если хотя бы по одному из второстепенных критериев оптимизации он не удовлетворяет неравенству отсекает часть множества q всех путей графа: путь отсекается – вычеркивается из перечня, полученного в п.2, если хотя бы по одному из второстепенных критериев оптимизации он не удовлетворяет неравенству 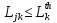 - если оптимизация k-го критерия предусматривает его минимизацию и неравенству - если оптимизация k-го критерия предусматривает его минимизацию и неравенству 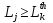 если оптимизация k-го критерия предусматривает его максимизацию. если оптимизация k-го критерия предусматривает его максимизацию.Неравенства могут быть строгими – в том случае, если длина пути, равная пороговой не включается в множество путей, прошедших порог. 4) Таким образом множество всех путей q проверяется на соответствие ограничениям по каждому из второстепенных критериев. Остаются лишь те пути, которые удовлетворяют всем ограничениям, т.е. прошли пороги по всем второстепенным критериям. Обозначим это множество 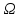 5) На множестве 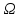 проводим однокритериальную оптимизацию по программе AMACONT, т.е. из множества путей проводим однокритериальную оптимизацию по программе AMACONT, т.е. из множества путей  выбираем тот, который содержит наилучший показатель основного (главного) критерия (к примеру, если это себестоимость С, то минимальное значение) выбираем тот, который содержит наилучший показатель основного (главного) критерия (к примеру, если это себестоимость С, то минимальное значение)Задание Необходимо выполнить следующие оптимизационные расчеты в среде MS Excel: 1) Однокритериальную оптимизацию: - по первому критерию; - по второму критерию; 2) Многокритериальную оптимизацию: - по обобщенному критерию, приняв 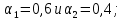 - пороговую, приняв в качестве основного 1-й критерий, пороговые значения 2-го критерия (второстепенного) взять соответствующими базовому варианту технологического процесса (путь выделен утолщенными ребрами). Условие Нам задана таблица 1 и граф №5. Таблица 1 – Значение критериев оптимизации
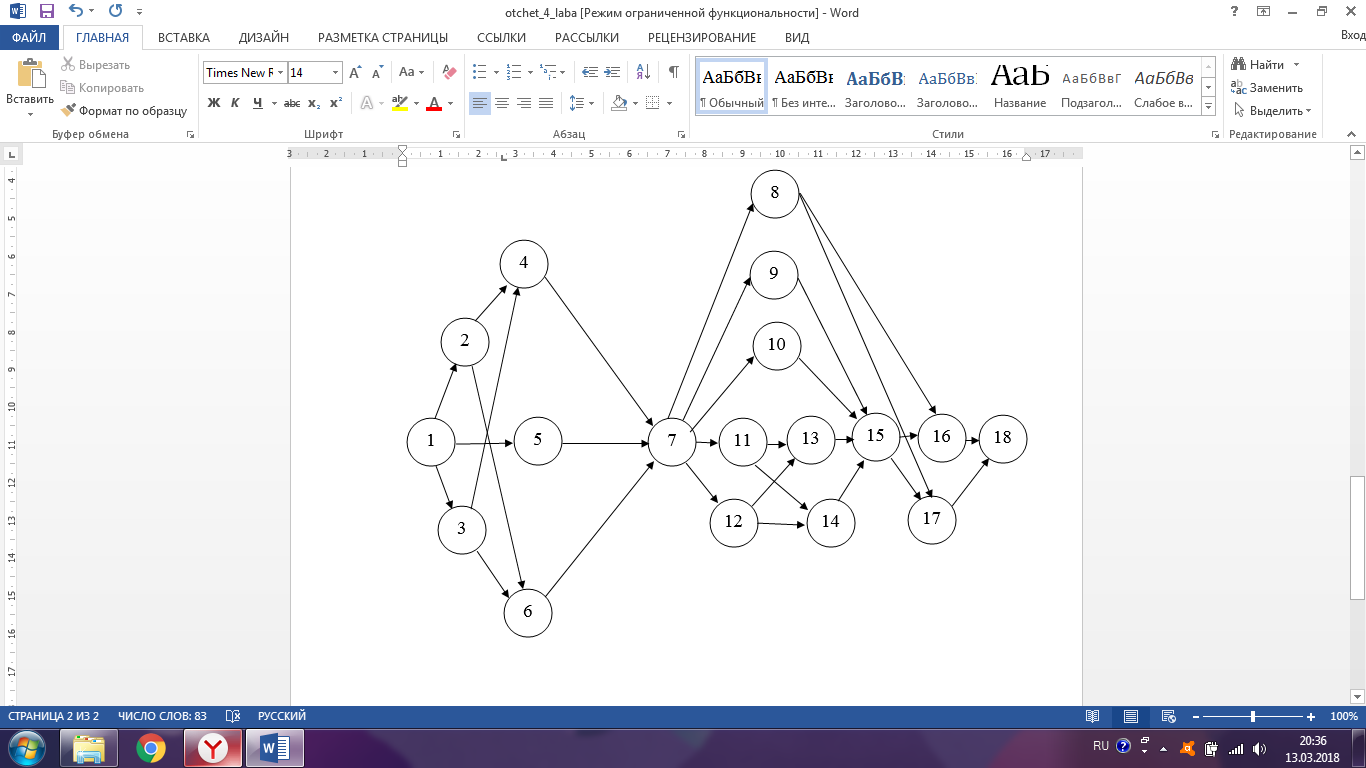 Ход работы Однокритериальная оптимизация Для начала, заполним нашу таблицу 1 в программе MS EXCELL Таблица 1 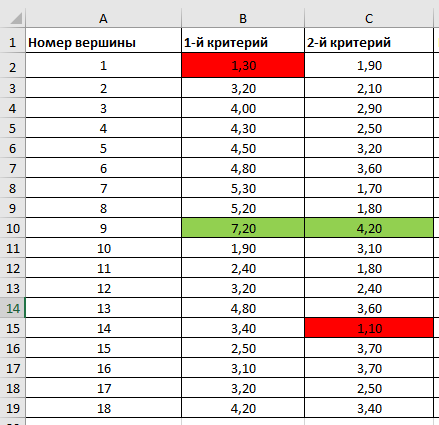 После этого, мы сделаем таблицу (табл. 1.11) в MS EXCELL, рассчитывая всевозможные комбинации путей из вершины 1 в вершину 17. Далее, мы найдем длины путей по 1 и 2 критериям, просуммировав соответствующие ячейки. Таблица 1.11 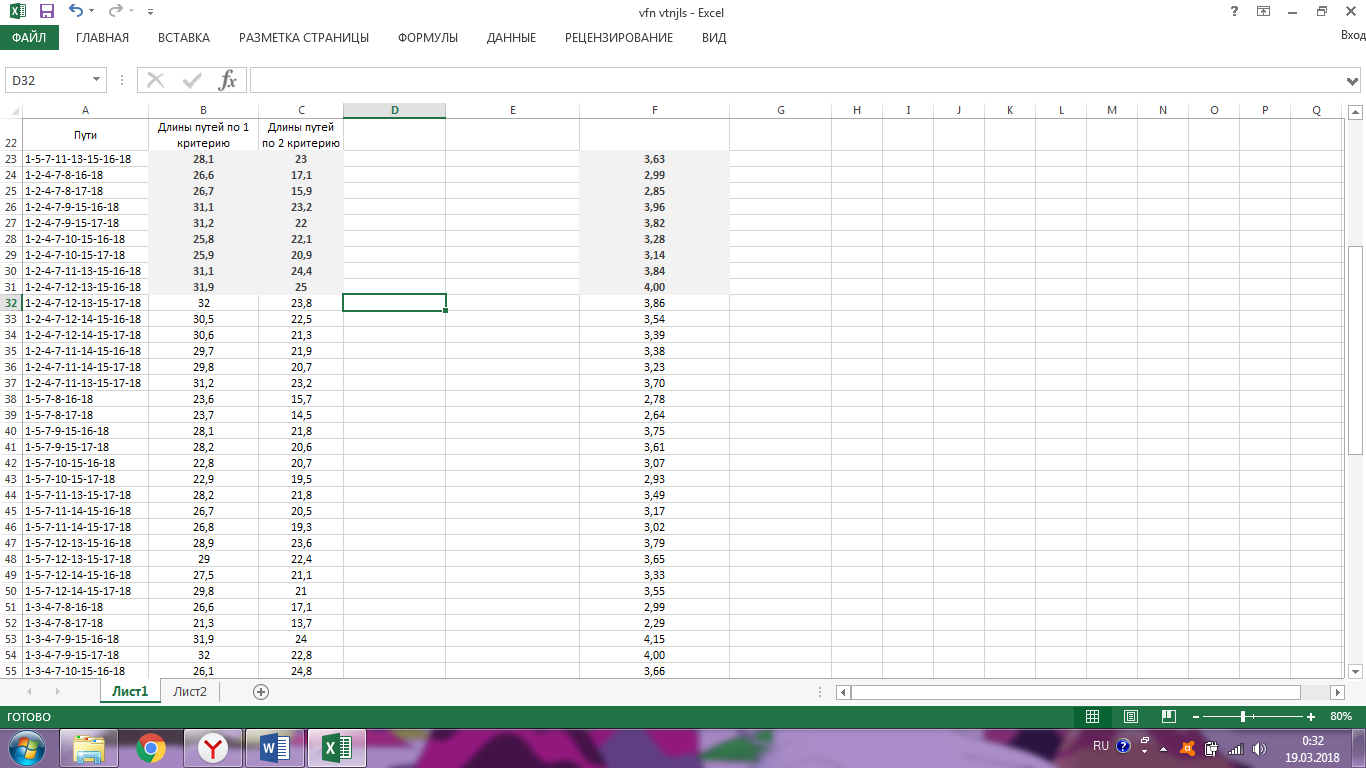 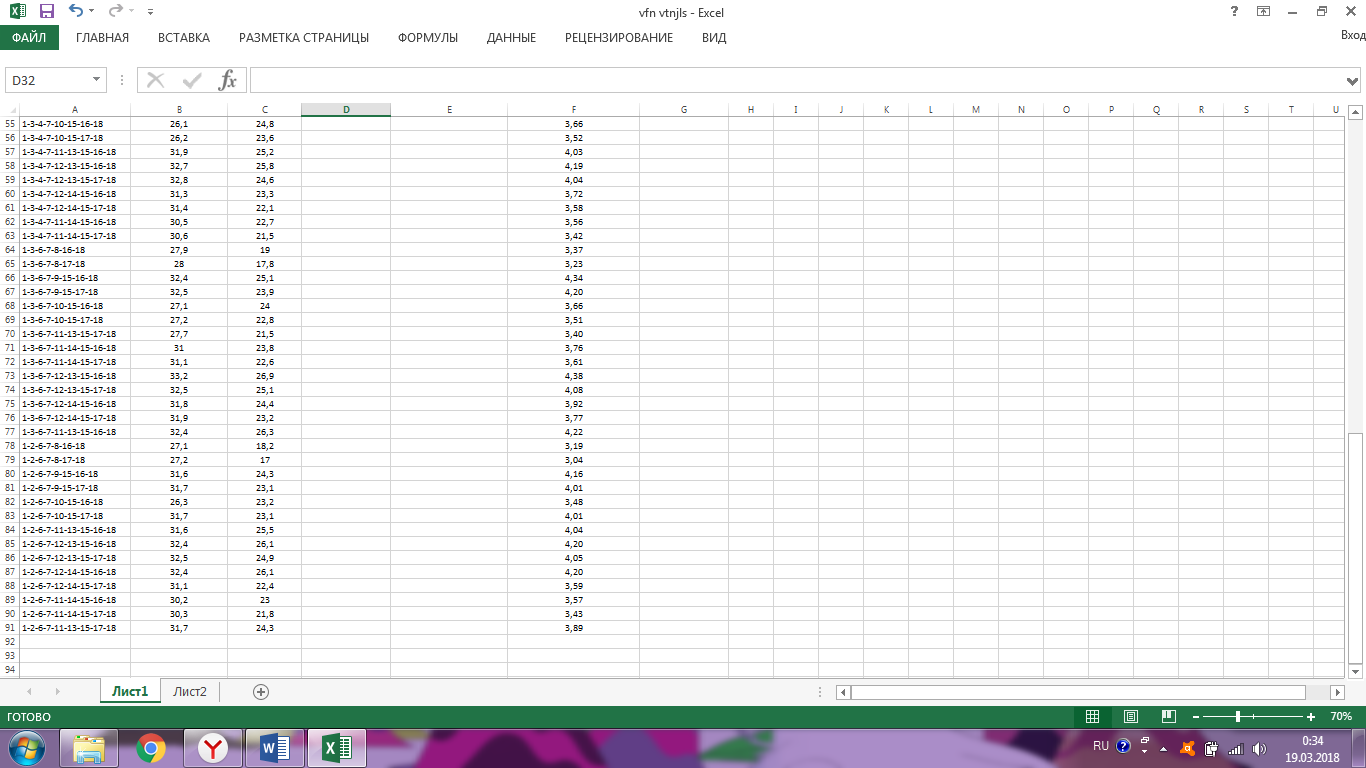 После того, как найдем длины, выполним однокритериальную оптимизацию по 1 критерию (по сумме) и по 2 критерию (по часам), для этого найдем минимальные значения: 1) По 1 критерию (по сумме) – это путь, под ячейкой А22 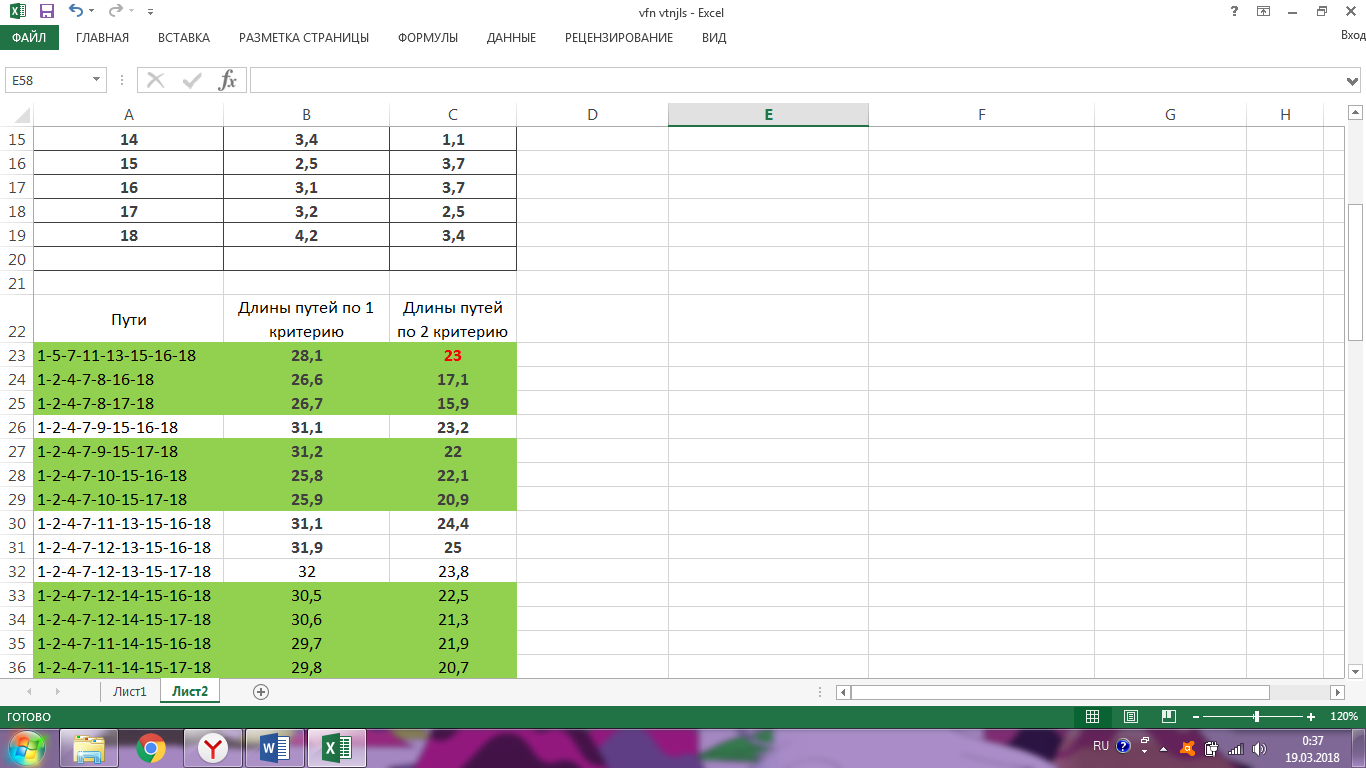 2) По 2 критерию (по часам) – это путь, под ячейкой А42 Многокритериальная оптимизация Многокритериальная оптимизация по обобщённому критерию Чтобы выполнить многокритериальную оптимизацию по обобщённому критерию, воспользуемся самой первой таблицей (табл.1). Для выполнения этой оптимизации, введем безразмерные величины. Для этого, в 1 и 2 критериях выделим минимальные и максимальные элементы. Таблица 1 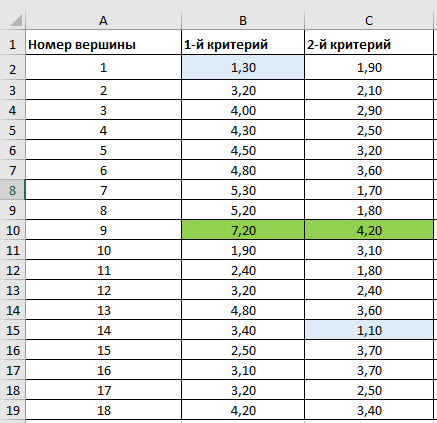 Для 1 критерия, max=7,20 (ячейка В10); min=1,30 (ячейка В1) Для 2 критерия, max=4,20 (ячейка С10); min=1,10 (ячейка С15) После этого построим новую таблицу (табл.1.12) с безразмерными величинами. Используем формулу:  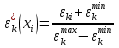 Так же, строим таблицу (табл.1.12) с обобщенным критерием, использую формулу: 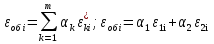 Где примем 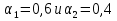 Таблица 1.12 Таблица 1.13 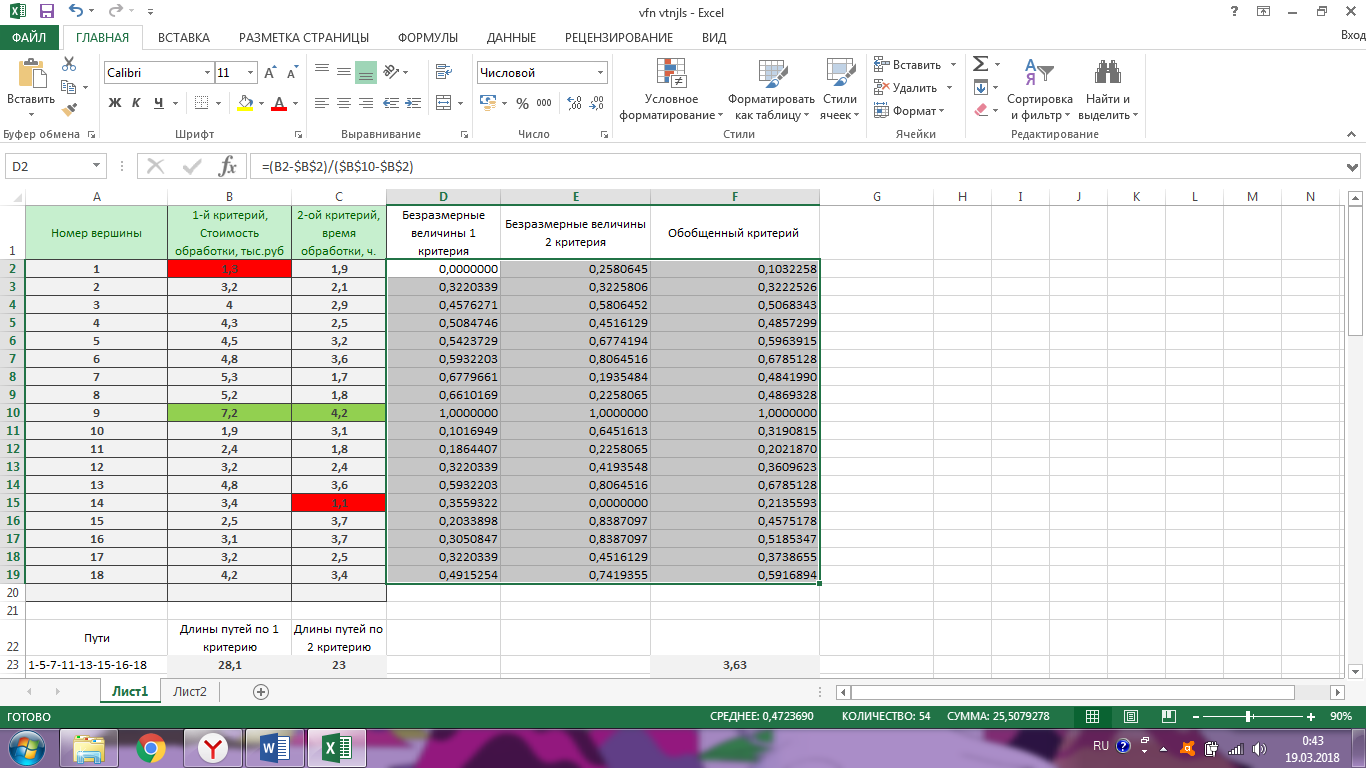 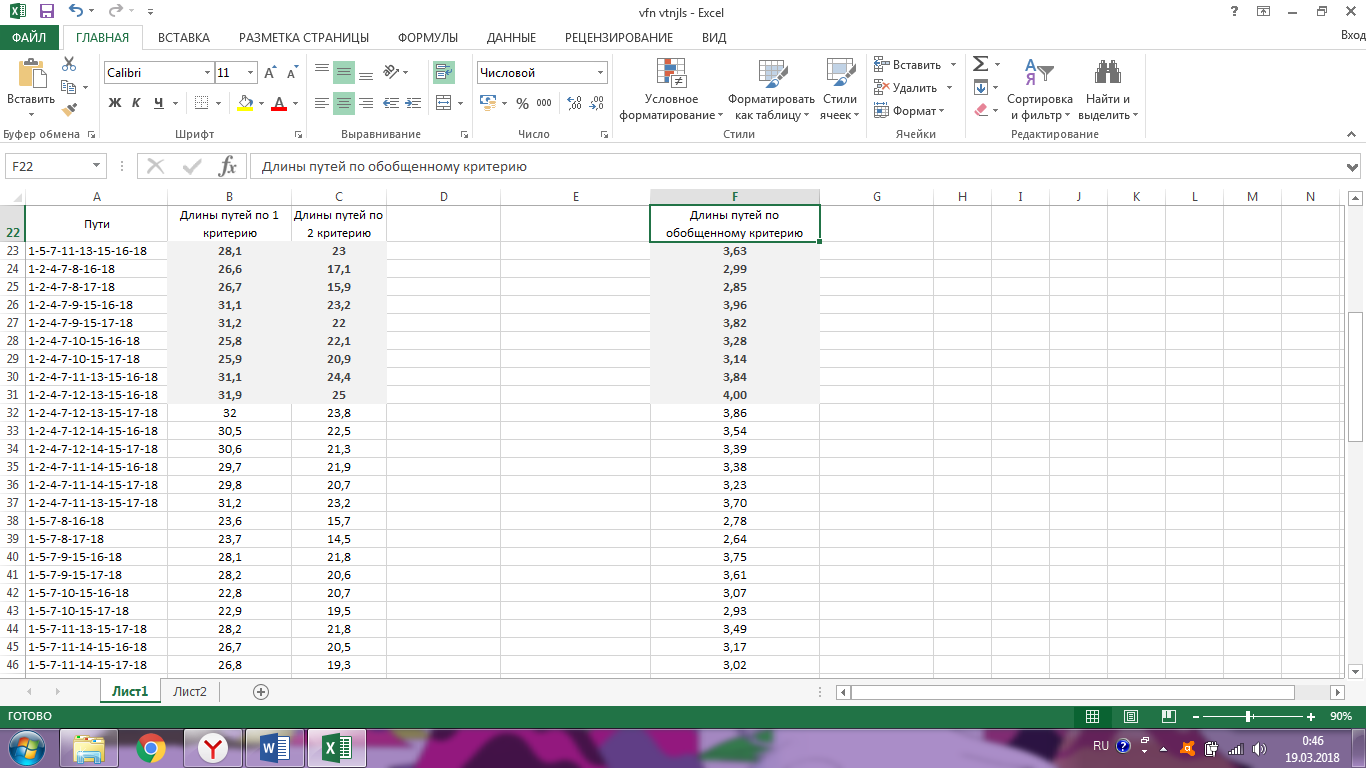 Последним шагом многокритериальной оптимизации по обобщённому критерию будет построение таблицы длины (табл.1.13) с обобщенным критерием. Для этого мы просуммируем соответствующие ячейки столбца F. Здесь, мы так же выберем ячейку с наименьшим значением - ячейка F22. Пороговая многокритериальная оптимизация Чтобы выполнить пороговую многокритериальную оптимизацию, скопируем таблицу 1 и таблицу 1.11 на новый лист в MS Excell. В качестве порогового значения, выступает значение длины 2 критерия, путь 1-4-6-9-10-12-14-17 (задано по условию): Следующим шагом, сортируем длины 2-го критерия, которые меньше порогового значения. Далее выбираем из всех сортируемых значений самое минимальное, в нашем случае это ячейка С42: В результате получим таблицу 1.14 Таблица 1.14 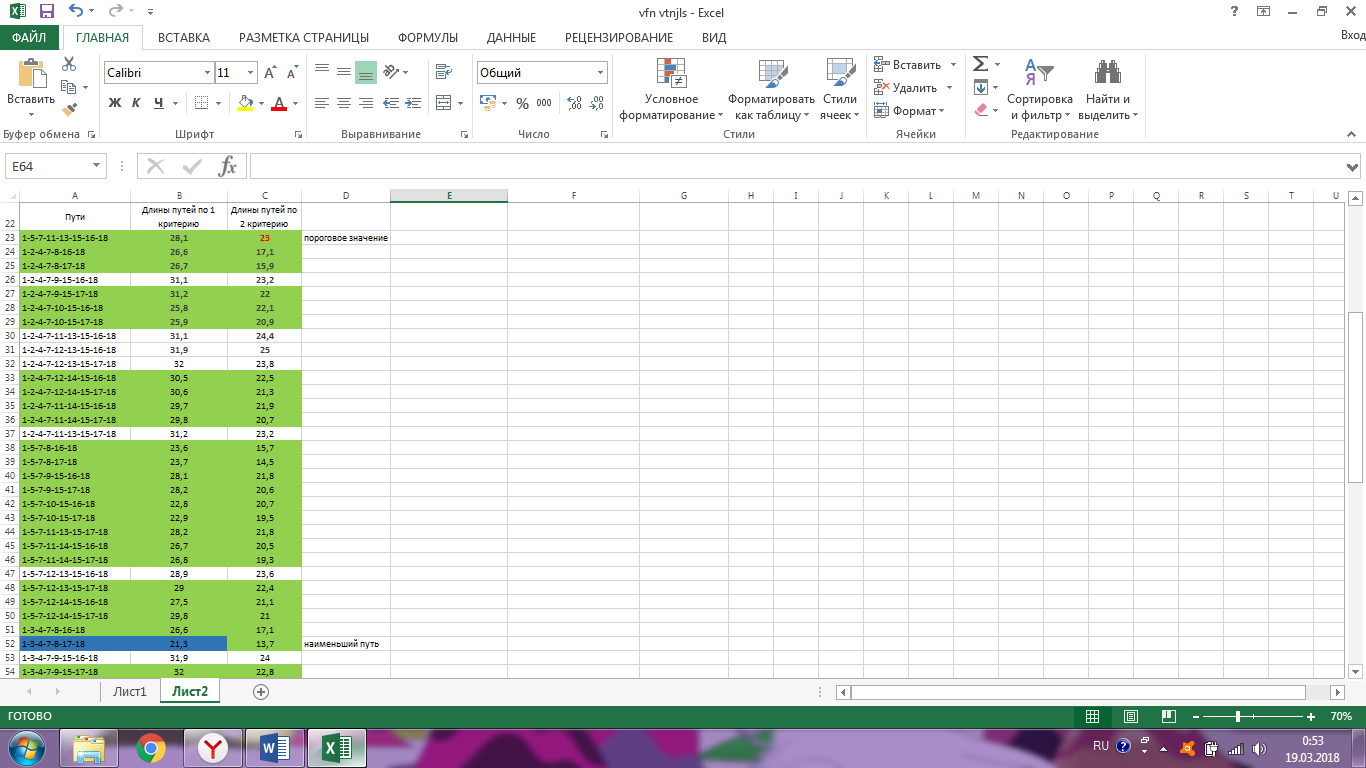 Выводы В ходе лабораторной работы, мы ознакомились с методами оптимизации процессов и получили практические навыки проведения оптимизации технологических процессов на различных иерархических уровнях по различным критериям. Мы провели однокритериальную оптимизацию по первому и второму критериям, и так же провели многокритериальную оптимизацию по обобщённому критерию и пороговую оптимизацию. |
