Отчет по лабораторной работе 1 по дисциплине Методы анализа динамических систем
 Скачать 101.01 Kb. Скачать 101.01 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Дальневосточный федеральный университет»
Кафедра электроэнергетики и электротехники ОТЧЕТ по лабораторной работе №1 по дисциплине «Методы анализа динамических систем» на тему «Исследование типовых динамических звеньев» Выполнил студент гр. Б3117-13.03.02ээсс А.И. Никифоров Проверил преподаватель, к.т.н. К.В. Чупина ____________________________ (зачет/незачет) «___» ____________2019 г. г. Владивосток 2019 Исходные данные и задание на работу Для заданных схем: определить передаточную функцию, изобразить амплитудно-фазовую характеристику, изобразить логарифмическую амплитудно-частотную характеристику, изобразить логарифмическую фазочастотную характеристику показать графики изменения переходных процессов при изменении параметров ПФ, сделать вывод о влиянии постоянной во времени и коэффициента передачи для каждого графика. Номиналы каждого элемента отображены соответственно на схемах, изображенных на рисунках 1 и 2. Все графики и вычисления проведены в программном продукте Mathcad 14 M035. 2.1. Передаточная функция Передаточной функцией называют один из способов математического описания динамической системы. Для определения передаточной функции необходимо выразить 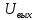 и и 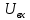 , для этого опишем первую схему по 2 закону Кирхгофа и переведём величины в операторную форму, учитывая, что , для этого опишем первую схему по 2 закону Кирхгофа и переведём величины в операторную форму, учитывая, что 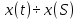 , где , где 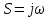 . .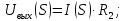 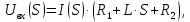 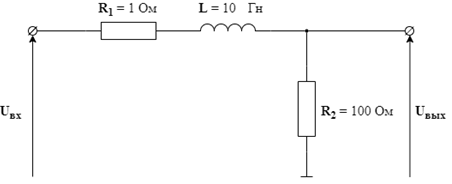 Рисунок 1 – Исследуемая схема №1 Тогда передаточная функция 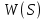 для первой схемы будет равна: для первой схемы будет равна: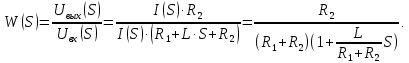 Сделаем замену, где постоянная во времени 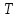 равна равна 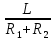 , а коэффициент передачи K равен , а коэффициент передачи K равен 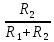 . Тогда передаточная функция для первой схемы . Тогда передаточная функция для первой схемы 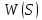 будет иметь следующий вид: будет иметь следующий вид: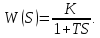 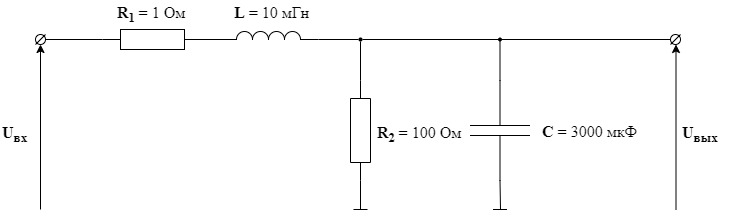 Рисунок 2 – Исследуемая схема №2 Подобные преобразования необходимо сделать, описав вторую схему и тогда мы получим, что: 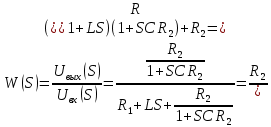 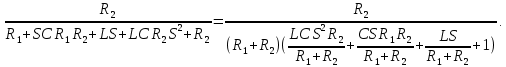 Сделаем замену, где постоянные во времени: 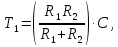 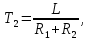 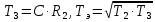 . .коэффициент передачи: 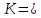 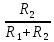 . .коэффициент колебательности: 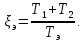 Тогда передаточная функция для второй схемы 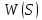 будет иметь вид: будет иметь вид: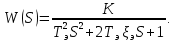 Для искусственных характеристик первой схемы примем, что 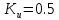 , а , а 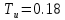 ; для второй соответственно: ; для второй соответственно: 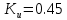 , , 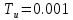 и и 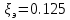 . .2.2. Амплитудно-фазовая характеристика Амплитудно-фазовая частотная характеристика – удобное представление частотного отклика линейной стационарной динамической системы в виде графика в комплексных координатах. Математически представляет собой функцию: 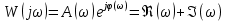 . .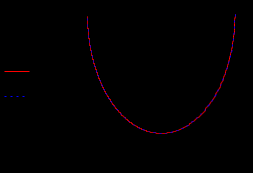 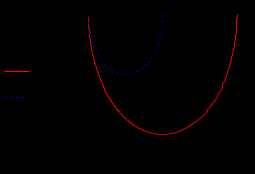 Рисунок 3 – АФХ при изменении величин ПФ для схемы №1 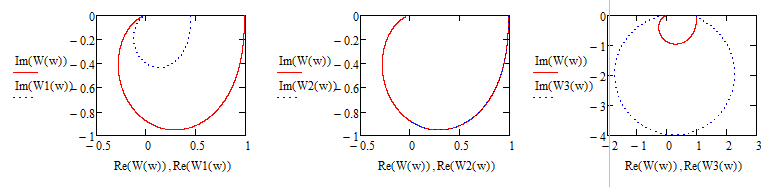 Рисунок 4 – АФХ при изменении величин ПФ для схемы №2 Стоит отметить, что вид амплитудно-фазовой характеристики не зависит от изменения постоянной во времени 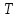 . . Изменяя частоту в диапазоне от 0 до 1000 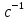 и соответственно коэффициент передачи звена и соответственно коэффициент передачи звена 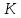 (практически в два раза) мы можем построить на комплексной плоскости график вектора АФХ – его годограф, представляющий собой полуокружность, расположенную в 4 квадранте комплексной плоскости, диаметр которой как раз и будет зависеть от (практически в два раза) мы можем построить на комплексной плоскости график вектора АФХ – его годограф, представляющий собой полуокружность, расположенную в 4 квадранте комплексной плоскости, диаметр которой как раз и будет зависеть от 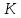 . .Коэффициент колебательности характеризует колебательность переходного процесса колебательного звена: чем он меньше, тем больше диаметр годографа. 2.3. Логарифмическая амплитудно-частотная характеристика Данная характеристика определяется как: 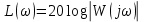 и по своей сути является зависимостью модуля коэффициента усиления (напряжения, тока или мощности) устройства от частоты в логарифмическом масштабе. и по своей сути является зависимостью модуля коэффициента усиления (напряжения, тока или мощности) устройства от частоты в логарифмическом масштабе.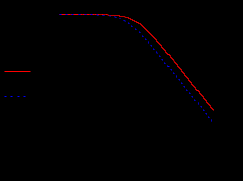 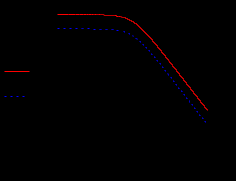 Рисунок 5 – ЛАЧХ при изменении параметров ПФ для схемы №1 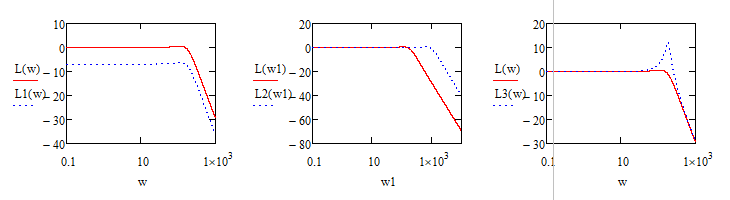 Рисунок 6 – ЛАЧХ при изменении параметров ПФ для схемы №2 Изменение постоянной во времени 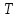 приводит к изменению частоты, а именно к смещению начальной наклонной точки графика. приводит к изменению частоты, а именно к смещению начальной наклонной точки графика.Коэффициент передачи звена определяет смещение от основной функции на графике. Чем меньше 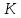 , то на ту же величину по основанию логарифма и будет смещен график логарифмической амплитудно-частотной характеристики вниз по оси ординат (изменение амплитуды). , то на ту же величину по основанию логарифма и будет смещен график логарифмической амплитудно-частотной характеристики вниз по оси ординат (изменение амплитуды).Изменение коэффициента колебательности приводит к появлениям резонансных явлений на характеристике. 2.4. Логарифмическая фазо-частотная характеристика Под данной зависимостью предполагают, что 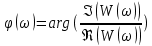 и по своей сути, это зависимость разницы фаз выходного и входного сигналов от частоты в полулогарифмическом масштабе. и по своей сути, это зависимость разницы фаз выходного и входного сигналов от частоты в полулогарифмическом масштабе.В проделанной нами работе, при изменении 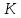 и и 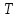 мы получили следующие графики: мы получили следующие графики: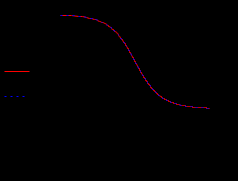 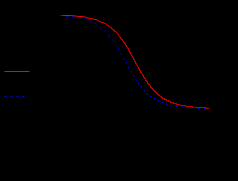 Рисунок 7 – ФЧХ при изменении параметров ПФ для схемы №1 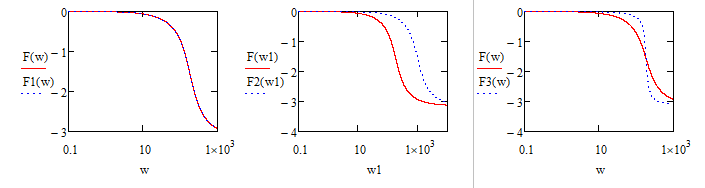 Рисунок 8 – ФЧХ при изменении параметров ПФ для схемы №2 Любое изменение коэффициента передачи звена никак не отображается на графике фазо-частотной характеристики, отсюда можно сделать вывод, что изменение сопротивлений, а именно самого 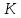 , не изменит форму и вид графика. , не изменит форму и вид графика.Изменение постоянной во времени 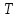 приведет к изменению частоты выходной фазы и смещению наклонной точки графика. приведет к изменению частоты выходной фазы и смещению наклонной точки графика.Изменение коэффициента колебательности приводит к уменьшению частоты среза, либо же к уменьшению полосы пропускания и подавления. 2.5. Переходные процессы Для прямой оценки качества системы управления используют кривую переходного процесса 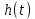 , которую характеризуют несколько числовых показателей: , которую характеризуют несколько числовых показателей: установившееся значение переходного процесса, максимальное значение процесса, перерегулирование, время регулирование или время переходного процесса 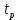 , отсчитываемое от момента приложения воздействия, , отсчитываемое от момента приложения воздействия,число перерегулирований, момент 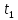 первого достижения уровня задания, первого достижения уровня задания,время достижение 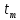 первого максимума. первого максимума.Кривую переходного процесса 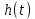 можно получить либо прямым путем, решая аналитически, или численными методами уравнения модели системы, либо косвенно, используя частотные и временные характеристики системы, путем построения некоторой ее аппроксимации. можно получить либо прямым путем, решая аналитически, или численными методами уравнения модели системы, либо косвенно, используя частотные и временные характеристики системы, путем построения некоторой ее аппроксимации. Алгоритмическим основанием для приближенного построения кривой переходного процесса является соотношение: 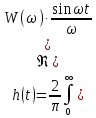 Используя наши данные, для первой схемы мы получили соответственно такие графики: 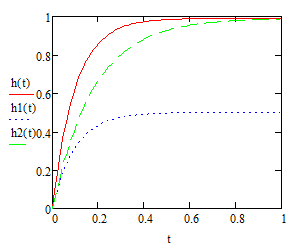 Рисунок 9 – Отображение переходных процессов при изменении параметров передаточной функции для 1 схемы Для второй: 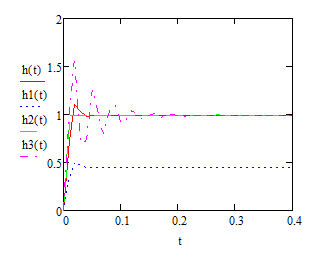 Рисунок 10 – Отображение переходных процессов при изменении параметров передаточной функции для 2 схемы Вывод: в проделанной лабораторной работе мы изучили типовые динамические звенья, а также экспериментально убедились в изменчивости характеристик в зависимости от различных значений параметров передаточной функции, например: при изменении коэффициента передачи 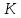 мы смещаем график от основного, либо же изменяем диаметр годографа (в случае с АФХ); при разных значениях постоянной во времени мы смещаем график от основного, либо же изменяем диаметр годографа (в случае с АФХ); при разных значениях постоянной во времени 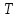 мы можем регулировать смещение наклонной точки графика; коэффициент колебательности задаёт графику появление резонансных явлений на характеристике, а приводит к уменьшению частоты среза, либо же к уменьшению полосы пропускания и подавления. мы можем регулировать смещение наклонной точки графика; коэффициент колебательности задаёт графику появление резонансных явлений на характеристике, а приводит к уменьшению частоты среза, либо же к уменьшению полосы пропускания и подавления. |
