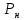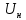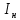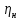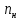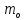СУЭП лаба 1. Отчет по лабораторной работе 1 Тема синтез модального регулятора и расчет переходных процессов в электроприводе постоянного тока
 Скачать 467.35 Kb. Скачать 467.35 Kb.
|
|
Министерство науки и высшего образования Российской Федерации  ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра электроэнергетики и электромеханики По дисциплине: Системы управления электроприводов (наименование учебной дисциплины согласно учебному плану) ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1 Тема: «СИНТЕЗ МОДАЛЬНОГО РЕГУЛЯТОРА И РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРОПРИВОДЕ ПОСТОЯННОГО ТОКА» Вариант №16 Автор: студент гр. ЭРБ-17 (шифр группы) (подпись) (Ф.И.О.) Оценка: Дата: Проверили: Руководитель работы: ассистент (должность) (подпись) (Ф.И.О.) Санкт-Петербург 2021 Цель работы заключается в изучении системы управления электроприводом постоянного тока с модальным регулятором координат на примере электропривода бурового станка Теоретические сведения: Структурная схема электропривода постоянного тока вращателя бурового става с модальным регулятором представлена на рис.1. Параметры электропривода принимаются в соответствии 16 варианта в табл.1. 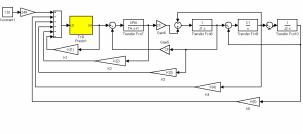 Рис 1 – Структурная схема с модальным регулятором Таблица 1
Таблица 2
Отрицательная обратная связь по координате объекта управления (ОУ) стабилизирует эту координату. Поэтому, если замкнуть ОУ по всем координатам, характеризующим его состояние в любой момент времени и называемым переменными состояния, то при соответствующем подборе коэффициентов обратных связей можно получить желаемые характеристики объекта управления относительно выходных координат. В общем случае ОУ имеет несколько: - входов U1, U2, …, Um; - выходов y1, y2, …, yr; - переменных состояния х1, х2, …, хn, где n - равно числу независимых дифференциальных уравнений, описывающих динамику ОУ . Сигналы обратных связей суммируются в модальном регуляторе в сигналы, образующие вектор UР(t) = [uр1, up2, …, upm]T, который подается на входы объекта управления, где вычитается из вектора задающих сигналов V(t) = [v1,v2, …,vm]T, в результате чего образуется вектор управляющих сигналов U(t) = [u1, u2, …, um]. Объект управления описывается системой дифференциальных уравнений в форме Коши: 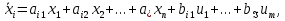 где i = 1, …, n; 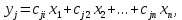 где j = 1, …, r. Уравнение модального регулятора и уравнение замыкания 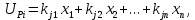 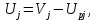 где j = 1, …, m. В матричной форме данные уравнения представляются в следующей форме: 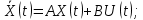 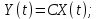 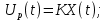 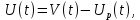 (1) (1)где А – квадратная матрица объекта управления ( 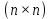 с элементом аij; с элементом аij; В – матрица управления 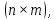 с элементом вij; с элементом вij;C – матрица выходов 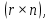 с элементом сij; с элементом сij;K – матрица модального регулятора 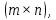 с элементом кij. с элементом кij.Проведя ряд преобразований с системой уравнений, получим результирующее матричное уравнение во временной области: 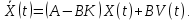 (2) (2)Уравнение (2) в операторной форме имеет вид 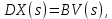 (3) (3)где D – характеристическая квадратная матрица 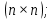 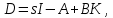 (4) (4) где I – единичная матрица. Детерминант от матрицы D является характеристическим полиномом замкнутого по вектору состояния объекта управления: 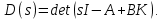 (5) (5)Решение характеристического уравнения D(s)=0 дает корни ОУ, замкнутого по вектору состояния. Отсюда вытекает принцип синтеза модального регулятора: подобрать матрицу К модального регулятора так, чтобы получить в комплексной плоскости желаемое распределение корней характеристического полинома замкнутого по вектору состояния объекта управления. Синтез МР выполняется методом стандартных уравнений, которые в нормированной форме приведены в справочной литературе. Процедура выполнения синтеза МР методом стандартных уравнений осуществляется в тир этапа: - определение количества и выбор переменных состояния, составление относительно выходной координаты характеристических уравнений для разомкнутого и замкнутого по вектору состояния ОУ; - выбор по желаемым показателям качества нормированного уравнения, порядок которого равен порядку уравнения ОУ; - определение параметров МР из системы уравнений 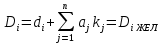 , (6) , (6)где i = 1,…, n. Синтез МР для приведенной системы электропривода (рис. 1) выполняется с использованием специальной программы в среде MATLAB «Вычисление коэффициентов оптимального регулятора [K]=lqry(sys,0.06,0.01)». Согласно процедуре синтеза выбираются переменные состояния: 1 - х1 = еП – ЭДС на выходе тиристорного преобразователя; 2 – х2 = iЯ - ток якоря двигателя; 3 – х3 = ω1– частота вращения якоря двигателя; 4 – х4 = М12– момент статических сопротивлений рабочего органа; 5 – х5 = ω2– частота вращения рабочего органа. 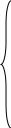 Далее составляются уравнения состояния, описывающих систему в форме Коши: Далее составляются уравнения состояния, описывающих систему в форме Коши: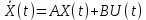 или в алгебраической форме: или в алгебраической форме: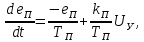 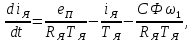 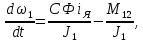 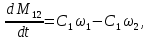 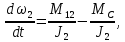 (7) (7)  где ТП = Тμ – электромагнитная постоянная времени тиристорного преобразователя. В соответствии системы уравнений (7) формируются матрицы А, В, С, D. где ТП = Тμ – электромагнитная постоянная времени тиристорного преобразователя. В соответствии системы уравнений (7) формируются матрицы А, В, С, D.   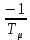 0 0 0 0 0 0 0 0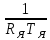 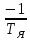 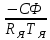 0 0 0 0А = 0 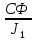 0 0 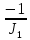 0 0 0 0 С1 0 - С1 0 0 0 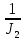 0 , 0 ,   В =[ В =[ 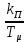 0 0 0 0 ], С = [0 0 0 0 1], D = [0]. 0 0 0 0 ], С = [0 0 0 0 1], D = [0].Ход работы: Для расчета параметров модального регулятора создаем m-файл, программа которого написана ниже: % Расчет оптимального регулятора для привода постоянного тока % Исходные данные % Двигатель 4ПФ180 P=37кВт CF=3.22; RA=0.344; TA=0.0139; J1=3; J2=0.05; C1=9570; % Динамическая система в пространстве состояний % dx/dt=Ax+Bu; % y=Cx+Du; A=[-100 0 0 0 0; 290.7 -71.9 -673.4 0 0; 0 1.07 0 -0.33 0; 0 0 9570 0 -9570; 0 0 0 20 0] B=[4400; 0; 0; 0; 0] C=[0 0 0 0 1] D=[0] % Сохранание динамической системы в пространстве состояний % под именем sys sys=ss(A,B,C,D) % Вычисление коэффициентов оптимального регулятора [K]=lqry(sys,0.06,0.01) 1. Произведем необходимые расчеты параметров электропривода в соответствии с исходными данными для расчета параметров из табл. 1. Тип двигателя 4ПФ180. При расчете принимаем следующие параметры: 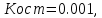 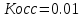 , , 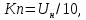 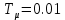 . . Расчет параметров двигателя: 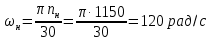 ; ; 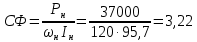 ; ; 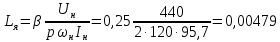 ; ; 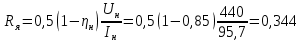 ; ; 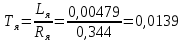 ; ; где р - число пар полюсов (принять р=2), 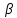 - коэффициент (принять - коэффициент (принять 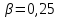 ). Момент инерции якоря двигателя ). Момент инерции якоря двигателя 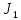 принимаем равным 3, т.к машинам большей мощности соответствует большее значение момента инерции. принимаем равным 3, т.к машинам большей мощности соответствует большее значение момента инерции.2. Рассчитаем параметры механической части привода. Вариант бурильной трубы указан в табл.1. Пользуясь табл. 2 рассчитать: - полярный момент сечения 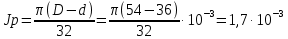 , ,где D - наружный диаметр буровой трубы; d - внутренний диаметр буровой трубы трубы. - крутильную жесткость буровой трубы 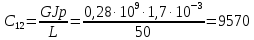 , ,где G - модуль сдвига; L = 50м – длина бурового става. - момент инерции бурового става 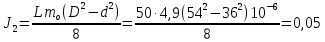 , ,где m0 - масса погонного метра трубы. 3. В модель системы вводим рассчитанные параметры МР и производим моделирование динамических процессов в модальном электроприводе. Затем производим такое же моделирование в системе с подчиненным регулированием параметров и оценим показатели качества переходных процессов при двух способах регулирования. Изменением общего коэффициента усиления усилительного звена после константы задания, добиваемся равенства установившихся значений переходных процессов. 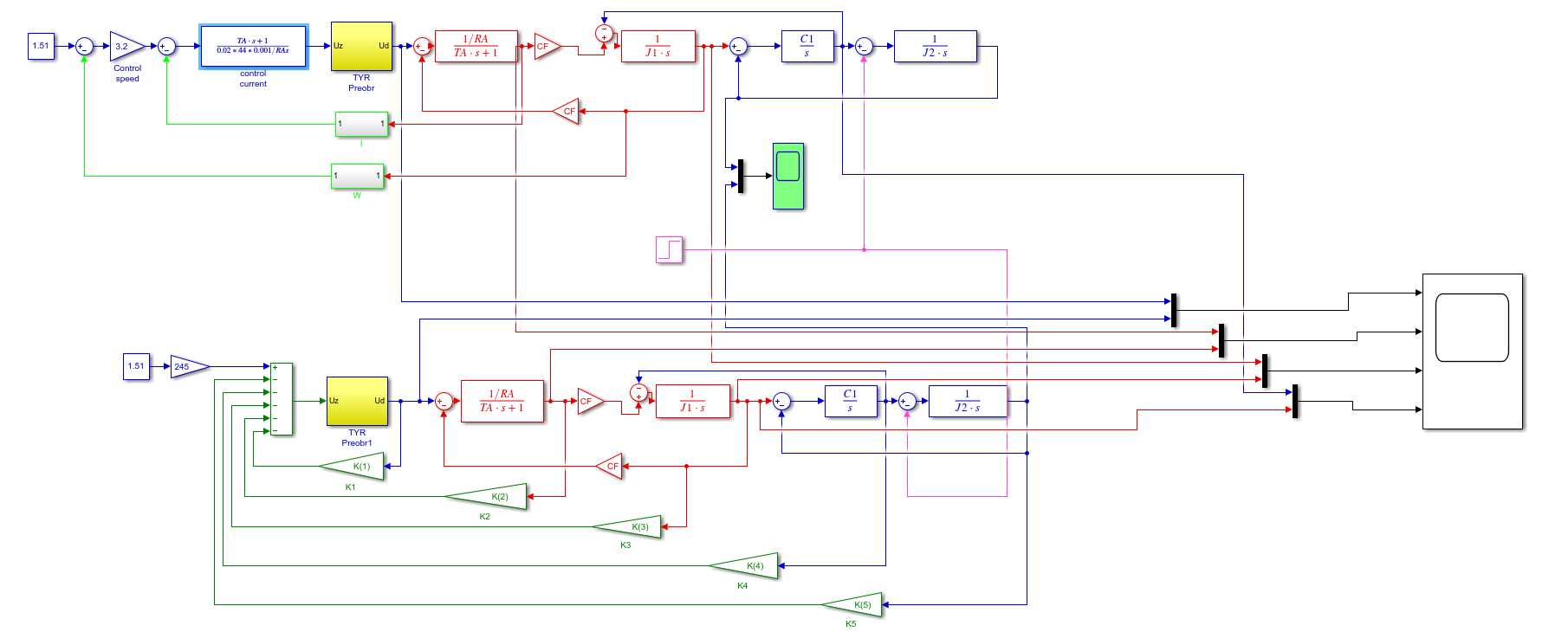 Рис.2 – Модель модального и подчиненного регулирования параметров  Рис.3 – Показания блока Scope Показатели качества переходного процесса: Время регулирования tр характеризует быстродействие системы и определяется следующим образом:  откладывается вверх и вниз от линии установившегося значения, образуется полоса, равная откладывается вверх и вниз от линии установившегося значения, образуется полоса, равная  . Время, при котором кривая переходной характеристики в последний раз входит в полосу . Время, при котором кривая переходной характеристики в последний раз входит в полосу  , считается временем регулирования. В данном случае время регулирования tр=0,8 с для модального регулирования и tр=0,19 с для подчиненного. , считается временем регулирования. В данном случае время регулирования tр=0,8 с для модального регулирования и tр=0,19 с для подчиненного.Перерегулирование определяется по формуле 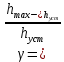 , , где 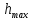 - максимальное значение регулируемой величины в переходном процессе. Перерегулирование получилось при подчиненном регулировании - максимальное значение регулируемой величины в переходном процессе. Перерегулирование получилось при подчиненном регулировании 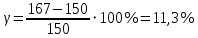 при модальном при модальном 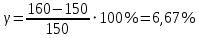 Качество управления считается удовлетворительным, если перерегулирование не превышает 40%. Качество управления считается удовлетворительным, если перерегулирование не превышает 40%.Колебательность  характеризуется числом колебаний регулируемой величины за время tр. Здесь колебательность равна трем в случае подчиненного регулирования и одному в случае с модальным. характеризуется числом колебаний регулируемой величины за время tр. Здесь колебательность равна трем в случае подчиненного регулирования и одному в случае с модальным.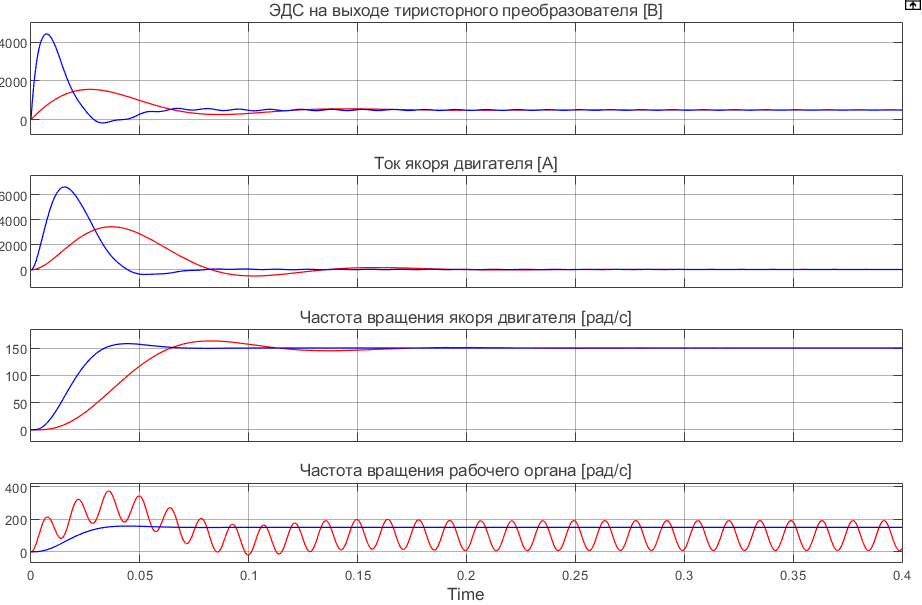 Рис.4 – Показания блока Scope при номинальной нагрузке 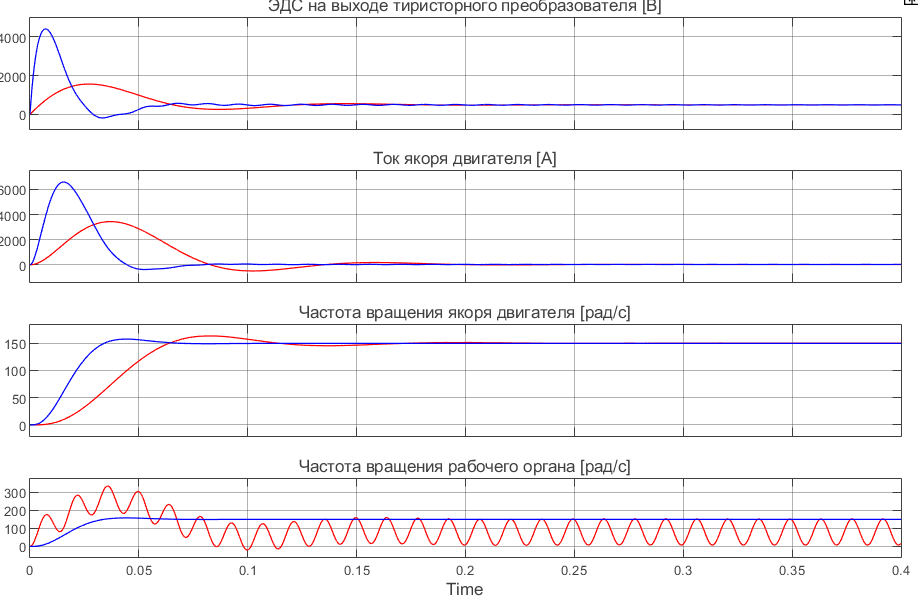 Рис.5 – Показания блока Scope при недогрузе (80% от номинального) 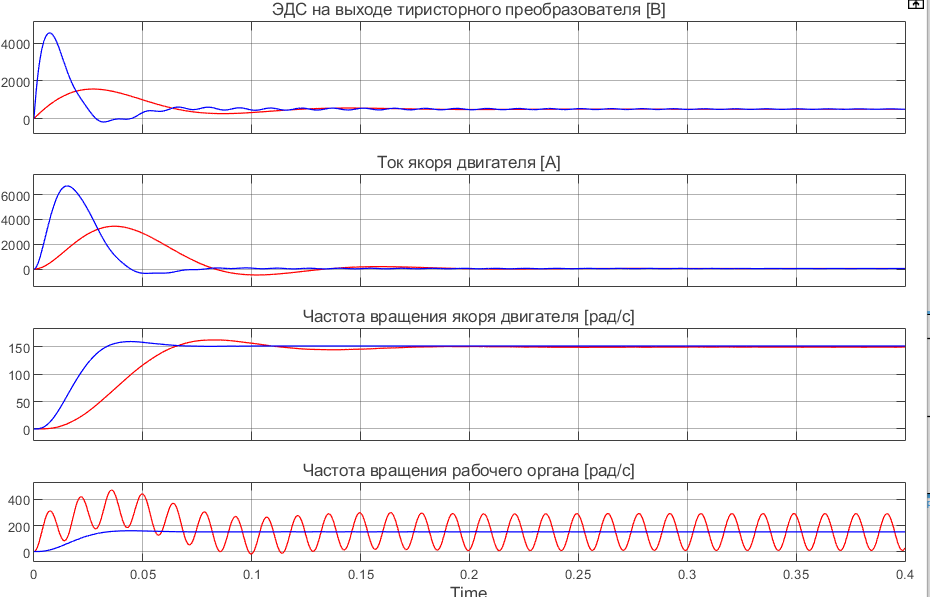 Рис.6 – Показания блока Scope при перегрузке (150% от номинального) 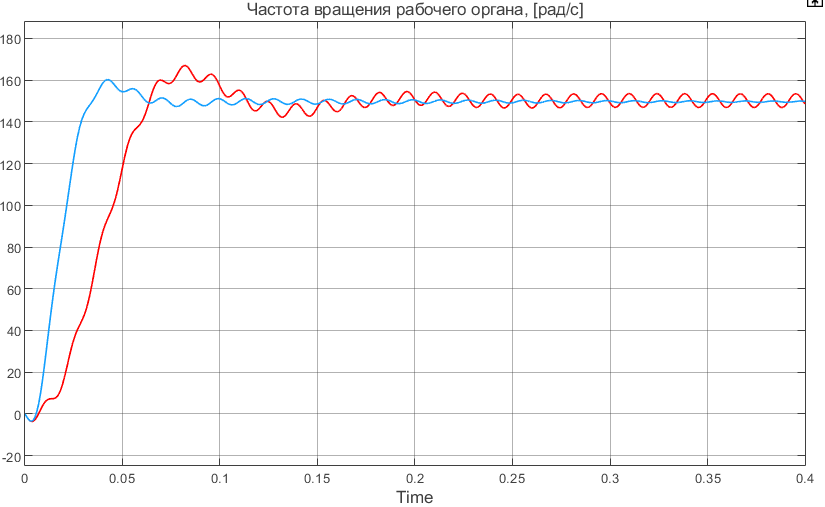 Рис.7 – Показания блока Scope при недогрузе (80% от номинального) 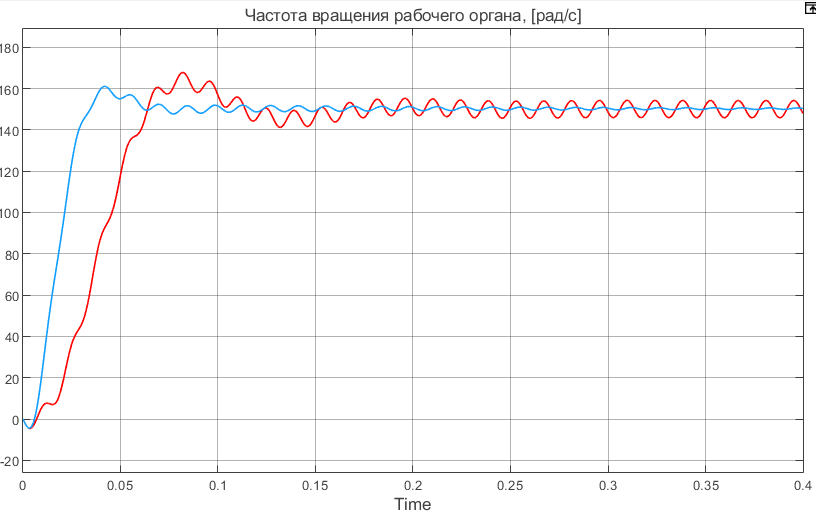 Рис.8 – Показания блока Scope при номинальной нагрузке 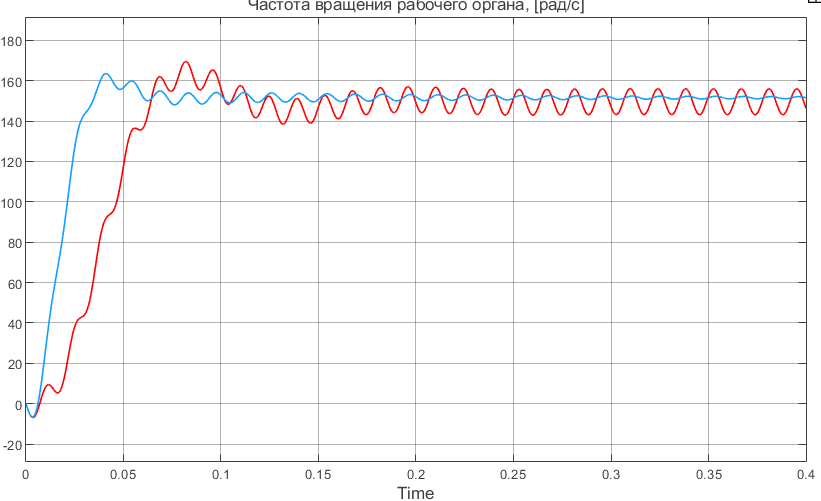 Рис.9 – Показания блока Scope при перегрузке (150% от номинального) Вывод: в ходе работы были рассмотрены переходные процессы в системе подчиненного регулирования и с МР. Система с МР имеет лучшие показатели качества (большее быстродействие, меньшее перерегулирование и меньшую колебательность) переходных процессов. При изменении нагрузки (80%, 100%, 150%) было установлено, что при увеличении нагрузки быстродействие падает, перерегулирование растет и существует большая колебательность процесса у процессов с подчиненным регулированием. В системах с МР показатели качества не изменяются. |