МиИОУ лаба № 1. Отчет По лабораторной работе 1 Вариант 4 По дисциплине Моделирование и идентификация объектов управления На тему Исследование линейных стационарных систем
 Скачать 0.51 Mb. Скачать 0.51 Mb.
|
|
Некоммерческое акционерное общество «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ» Кафедра «Автоматизация и управление» Отчет По лабораторной работе № 1 Вариант № 4 По дисциплине Моделирование и идентификация объектов управления На тему «Исследование линейных стационарных систем» Специальность «5В070200 – Автоматизация и управление Выполнил Бижанов Е.Г. Группа АИСУ-15-4 (Ф.И.О.) Принял ассистент Ташибаева А.Е. . (ученая степень, звание, Ф.И.О.) __________ ________________ «_____»________________2018 г. (оценка) (подпись) Алматы 2018 Лабораторная работа №1. Исследование линейных стационарных систем Цель работы: создание моделей динамических систем в командном окне MatLab; анализ моделей средствами пакета Control System Toolbox. Задание на лабораторную работуВ процессе выполнения лабораторной работы нужно: - создать модель системы в виде передаточной функции; - построить эквивалентные модели в пространстве состояний и в форме «нули-полюса»; - определить коэффициент усиления в установившемся режиме и полосу пропускания системы; - научиться строить импульсную и переходную характеристики, карту расположения нулей и полюсов, частотную характеристику; - научиться использовать пакет ControlSystemToolbox для построения различных характеристик; - научиться строить процессы на выходе линейной системы при произвольном входном сигнале. Выполнение заданий по лабораторной работе: 1) Номер варианта:
2) Очищаем рабочее пространство MatLab (память): clearall и очищаем окно MatLab: clc. 3) Смотрим краткую справку по команде tf: helptf. 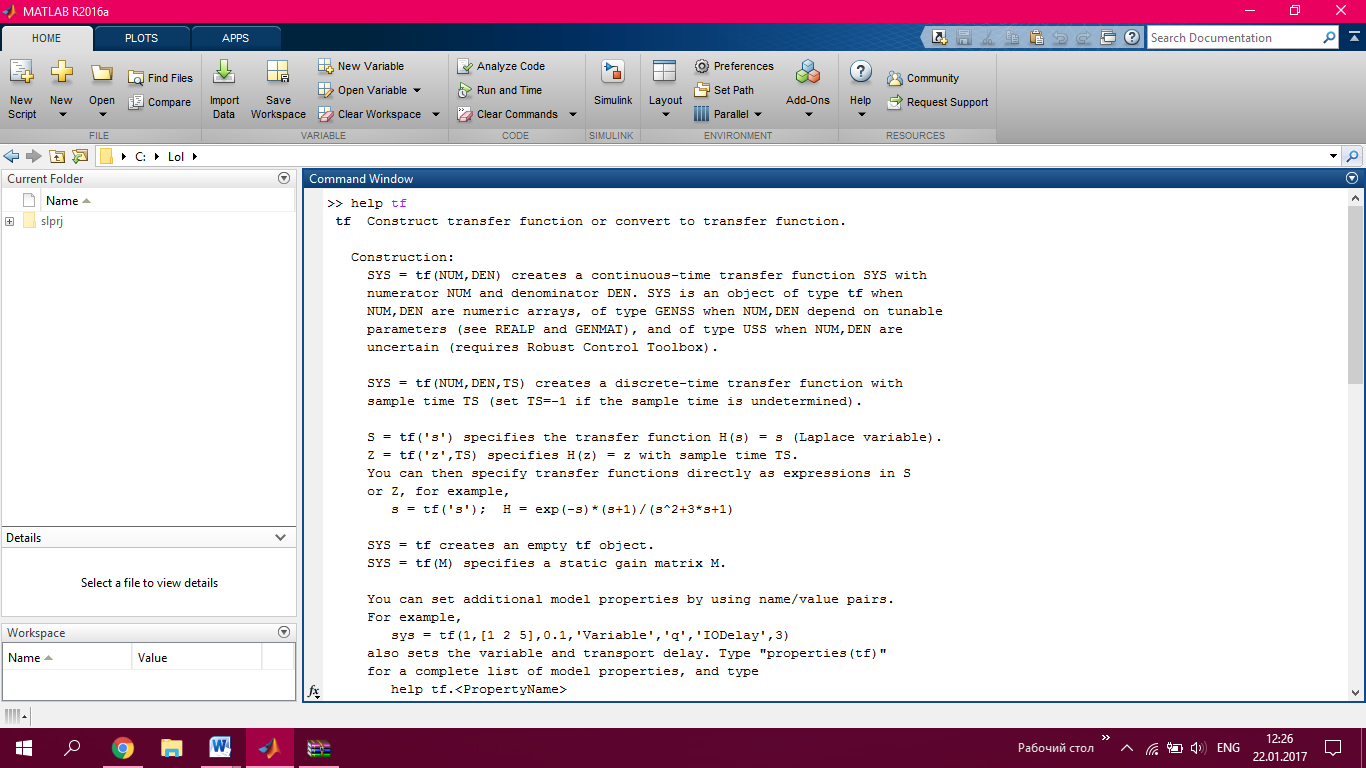 Рисунок 1 – Краткая справка по команде tf 4) В командном окне MatLab вводим вектора коэффициентов числителя num и знаменателя den передаточной функции (по варианту): 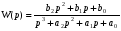 . . Рисунок 2 – Ввод векторов коэффициентов передаточной функции 5) Используя команду model = tf (num, den) создаем модель объекта.  Рисунок 3 – Создание модели объекта по векторам коэффициентов 6) Строим модель системы в пространстве состояний. Записываем систему уравнений для этой модели, используя полученные коэффициенты. 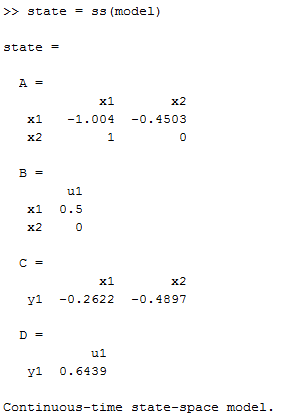  Рисунок 4 - Модель системы в пространстве состояний и ввод полученных матриц состояний 7) Находим нули и полюса передаточной функции. Знаменатель и числитель передаточной функции — это характеристические полиномы дифференциального уравнения движения линейной системы, где полюсами передаточной функции называют корни характеристического полинома знаменателя, нули — корни характеристического полинома числителя.  Рисунок 5 – Полюса и нули исходной передаточной функции 8) Cтроим модель исходной системы в форме «нули-полюса».  Рисунок 6 - Исходная функция в форме «нули-полюса» 9) Cтроим на графике расположение нулей и полюсов системы при помощи команды pzmap(model) 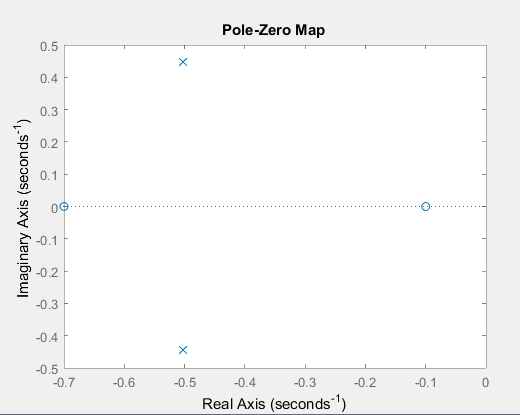 Рисунок 7 - График расположения нулей и полюсов 10) Преобразовываем непрерывную модель в дискретную  здесь 0.01 – шаг дискретизации, и обратно в непрерывную.  Рисунок 8 - Преобразование непрерывной модели в дискретную и обратно в непрерывную При обратном преобразовании получен исходный вариант модели. В результате этих действий в рабочей области сохранены три модели: model, disc, cont. 11) Находим коэффициент усиления звена в установившемся режиме. Объясняем, что определяет этот коэффициент. Коэффициент усиления показывает, во сколько раз изменится выходная величина по отношению к изменению входной величины в установившемся режиме.  Рисунок 9 - Коэффициент усиления звена в установившемся режиме 12) Определяем полосу пропускания системы (наименьшую частоту, на которой АЧХ становится меньше, чем - 3 дБ).  Рисунок 10 - Полоса пропускания системы 13) Определяем коэффициенты демпфирования и собственные частоты для всех элементарных звеньев (первого и второго порядка).   Рисунок 11 - Коэффициенты демпфирования и собственные частоты 14) В командной строке набираем ltiview. Выбираем в появившемся окне File/Import. Откроется диалоговое окно выбора модели для загрузки. Ваши модели тоже будут в этом списке. 15) Загружаем свою модельmodel. Появится окно с переходной характеристикой системы. 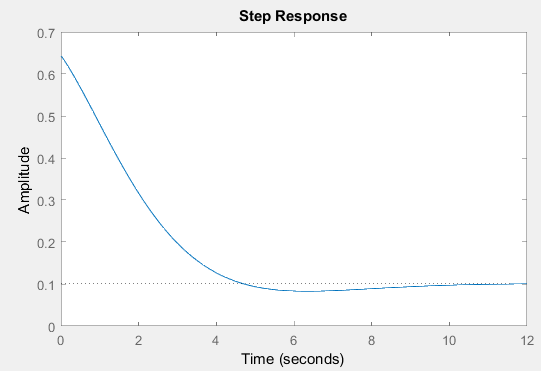 Рисунок 12 - Переходная характеристика системы 16) Строим импульсную характеристику (весовую функцию) этой системы: контекстое меню – PlotTypes – Impulse. 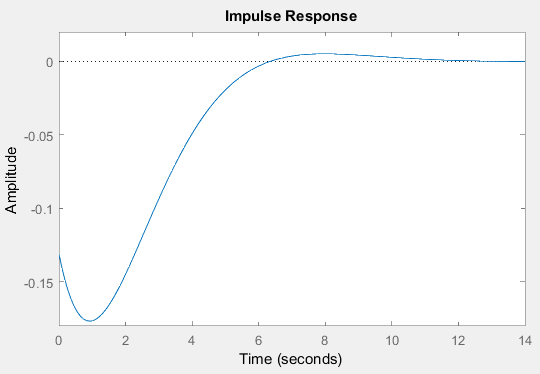 Рисунок 13 - Импульсная характеристика системы 17) Активизируем меню Edit/PlotConfiguration, что приведет к появлению диалогового окна, позволяющего выбрать набор интересующих характеристик для их отображения. Возможен выбор до 6 характеристик одновременно. Выбираем две характеристики: переходную и импульсную переходную функции. 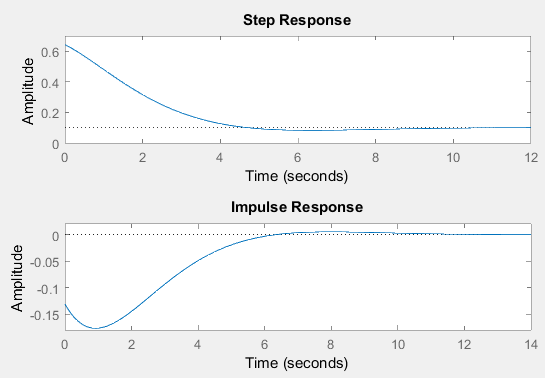 Рисунок 14 - Переходная и импульсная характеристики системы 18) На графике для каждой функции отмечаем: максимум, время переходного процесса, время нарастания (от 10% до 90% установившегося значения), установившееся значение: контекстое меню – Characteristics: 1. PeakResponse. 2. SettlingTime, 3. RiseTime, 4. SteadyState. И щелкая мышью по меткам-кружкам, выведите на экран рамки с численными значениями этих параметров и расположите их так, чтобы все числа были видны. 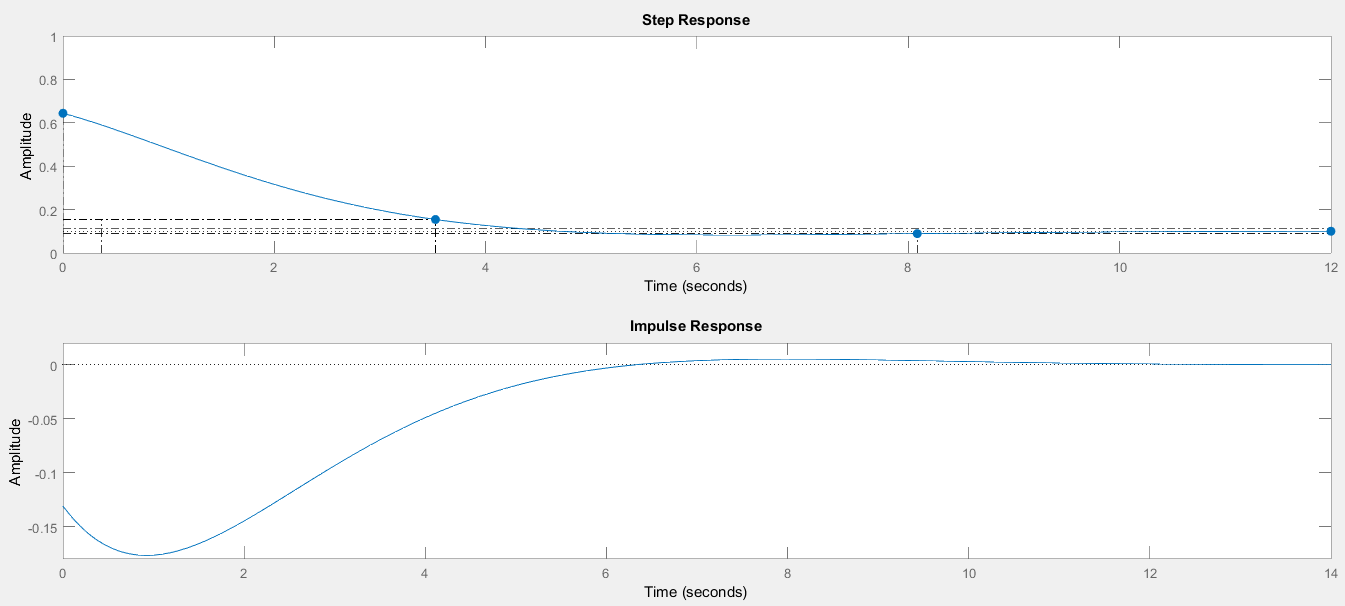 Рисунок 15 - Переходные характеристики с прямыми показателями качества 19) Закрываем окно LTIViewer. 20) Создаем массив частот для построения частотной характеристики (100 точек в интервале от 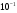 до до 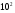 с равномерным распределением на логарифмической шкале): с равномерным распределением на логарифмической шкале): w = logspace(-1, 2, 100); 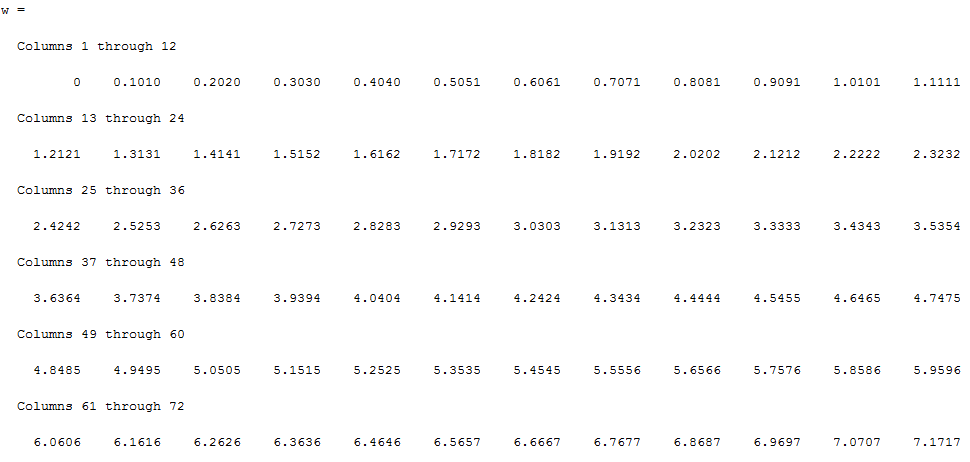  Рисунок 16 - Массив частот 21) Рассчитываем частотную характеристику исходной системы и строим ее на осях с логарифмическим масштабом по оси абсцисс. >> r = freqresp ( f, w );  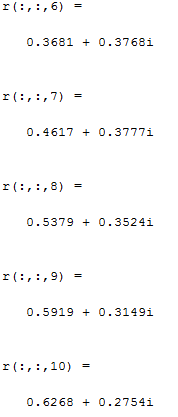              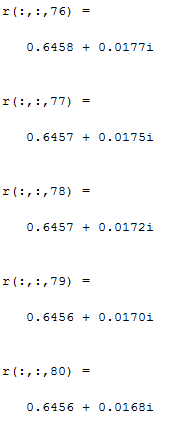  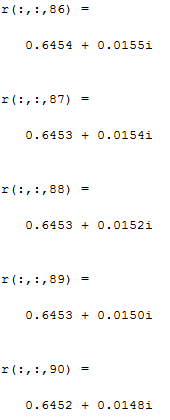 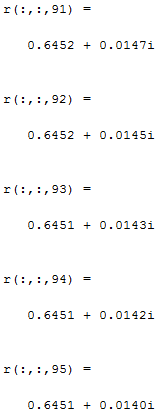  Рисунок 17 - Оператор обработки массивов  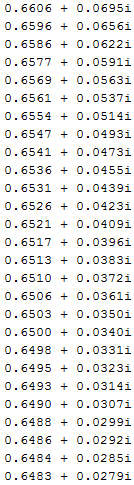   Рисунок 18 - Обработка одномерного массива 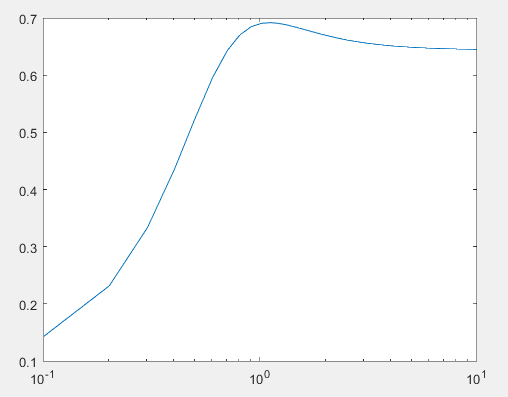 Рисунок 19 - Построение частотной характеристики в логарифмическом масштабе 22) Объяснить, где на графике можно найти коэффициент усиления в статическом режиме и как определить полосу пропускания системы. Коэффициент усиления в статическом режиме определяется значением, при котором переходная характеристика установилась. Так как в пункте 21 была построена логарифмическая амплитудно-частотная характеристика (ЛАЧХ), то для нахождения коэффициента усиления необходимо приравнять 20lgK=L1(ω), и выразить значение К. Полоса пропускания – это интервал частот, при котором выполняется условие 0,707А(0)≤А(ω). Заключение В данной лабораторной работе были изучены основные команды командного окна MatLab. Были созданы модели динамических систем, а также произведен подробный анализ моделей средствами пакета Control System Toolbox. Были получены навыки построения тех или иных графиков, на основе которых можно анализировать систему. В конце работы рассчитаны частотные характеристики исходные системы и построены на осях. Можно сказать, что командное окно MatLab удобная среда для анализа систем, с большой экономией времени и не требующая ручных расчетов. |
