МССУК лабораторная работа 2 (wecompress.com). Отчет по лабораторной работе 2 По дисциплине мссиУК
 Скачать 0.62 Mb. Скачать 0.62 Mb.
|
|
Некоммерческое акционерное сообщество «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ имени Гумарбека Даукеева»  Кафедра «Автоматизация и управление» Отчет по лабораторной работе №2 По дисциплине: МССиУК Специальность: Автоматизация и управление Выполнил: Еркинов Т. А. Группа: АУ-20-7 Вариант: 9 Приняла: Хан С. Г. ___________ ____________ «_____» __________2022 г. (оценка) (подпись) Алматы 2022 г. Цель работы: - ознакомление с методикой выполнения прямых измерений с многократными наблюдениями при наличии грубых погрешностей (промахов, выбросов). Получение применительно к этому случаю навыков обработки результатов наблюдений и оценивая погрешностей результатов измерений. Задание к лабораторной работе: - изучить структурные схемы и технические характеристики ТХА-2174 и КСП-2-07, представляемых на экране виртуальной лабораторной работы; - провести имитационный эксперимент по измерению заданной входной величины с помощью данных средств измерений; - провести статическую обработку результатов имитационного эксперимента; - оценить законы распределения погрешностей данных средств измерений; - проверить гипотезу о принадлежности результатов наблюдений нормальному распределению с помощью критерия согласия Пирсона. Задание: Провести статистическую обработку результатов измерения температуры t=260 °C, используя: 1) первичный преобразователь ТХА-2174; 2) вторичный прибор КСП-2-07 Определить значение критерия согласия Пирсона при P1=0,97; P2=0,93. Выполнение задания: Первичный преобразователь Первичный прибор по заданию – ТХА-2174. 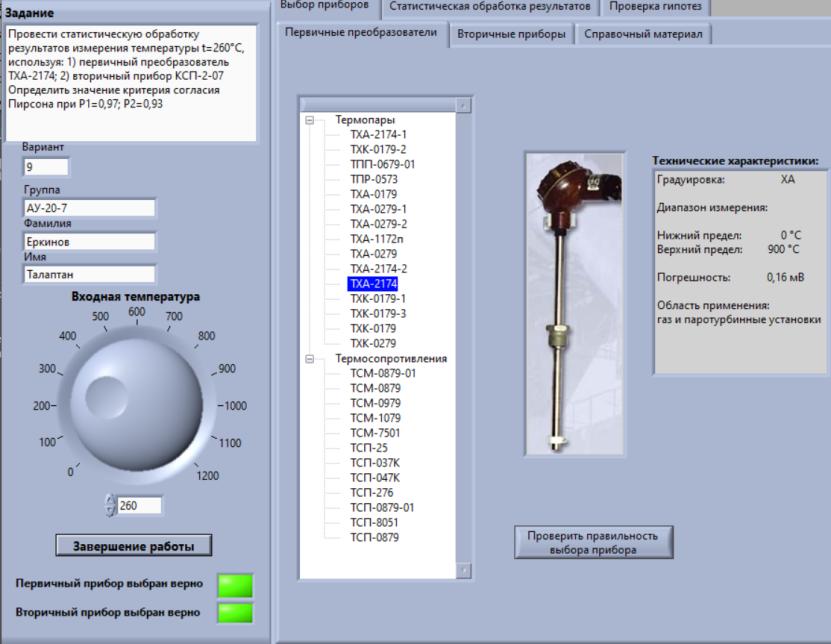 Рисунок 1. Выбор первичного преобразователя. После выбора прибора, нужно провести имитационный эксперимент на 25 случайных величин. 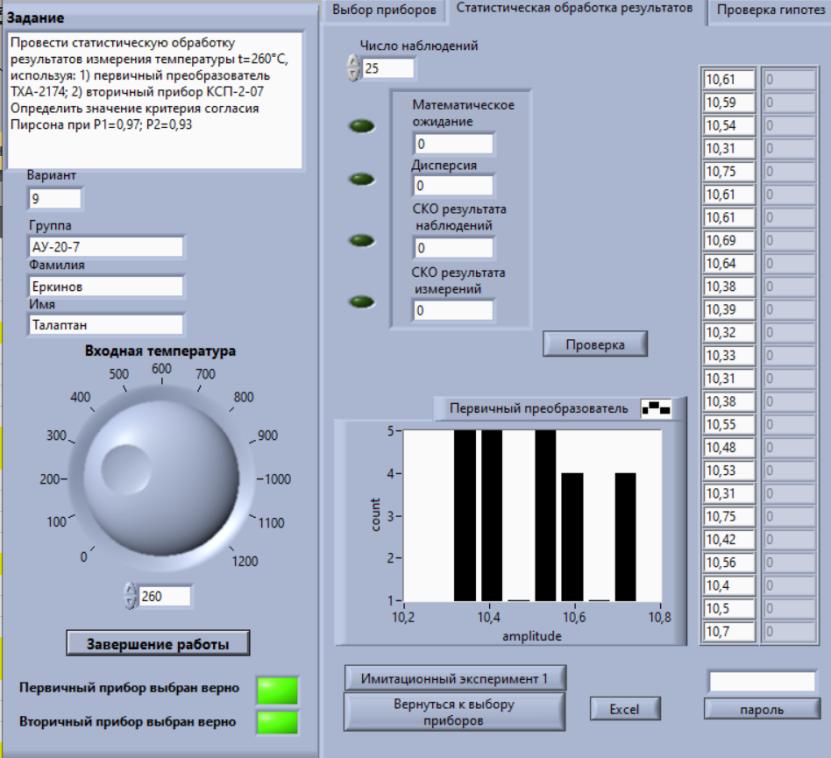 Рисунок 2. Получение 25 случайных величин. Далее, нужно провести статистический расчет полученных результатов, вычисления проводят в таблице Excel. 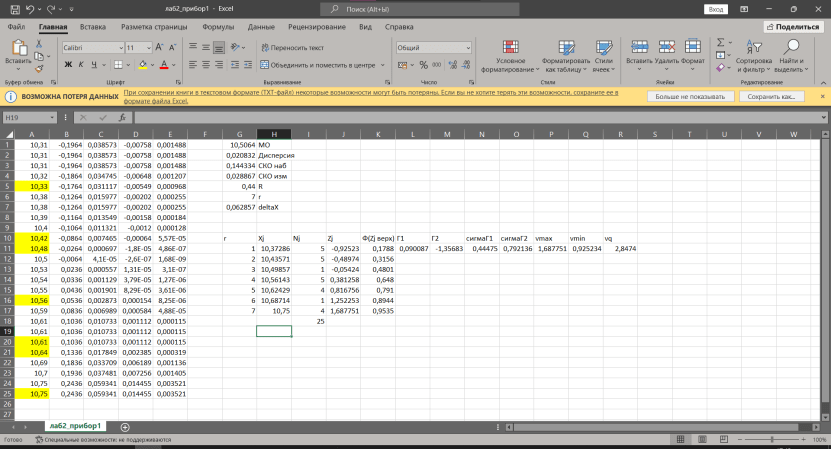 Рисунок 3. Расчет статистических результатов для первичного преобразователя. 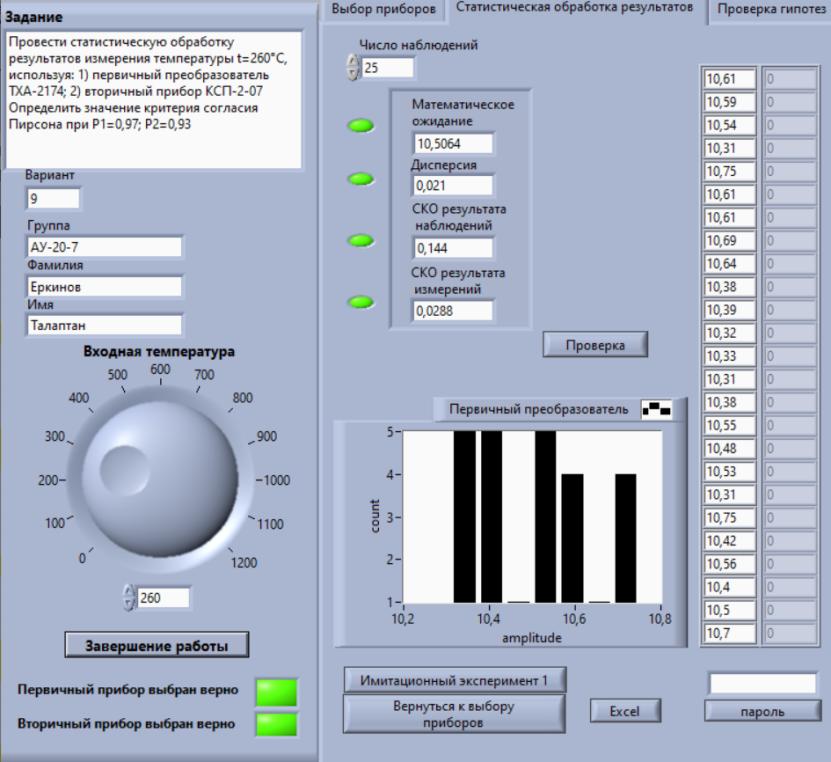 Рисунок 4. Проверка проведенных расчетов. Расчеты для первичного преобразователя а) Математическое ожидание: X = 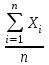 = 10,5 мВ; = 10,5 мВ;б) Дисперсия: D = S2 = 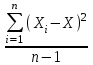 = 0,021 мВ; = 0,021 мВ;в) Среднеквадратическое отклонение наблюдения: 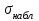 = =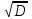 = 0,14 мВ; = 0,14 мВ;г) Среднеквадратическое отклонение измерения: 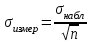 =0,028 мВ; =0,028 мВ;Проверка гипотезы о нормальном законе распределения по эмпирическим оценкам. Производим расчеты коэффициентов асимметрии и эксцесса для первичного преобразователя. Эмпирическая оценка Г1 коэффициента асимметрии: Г1= 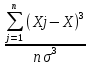 = 0,09 = 0,09Эмпирическая оценка Г2 коэффициента эксцесса: Г2= 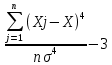 = -1,35 = -1,35Степень рассеяния для величин Г1 и Г2 может быть приближенно оценена путем сравнения их с оценкой среднего квадратического отклонения коэффициентов асимметрии 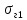 и эксцесса и эксцесса 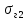 : :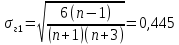 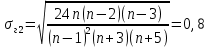 Распределение считают нормальным, если одновременно выполняются соотношения: 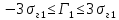 и и 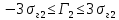 . .Для первичного преобразователя соотношения выполняются, т.е.: -1,335≤ 0,09≤2,376 для коэффициента асимметрии; -2,4≤-1,35≤2,4 для коэффициента эксцесса, следовательно закон распределения нормальный. 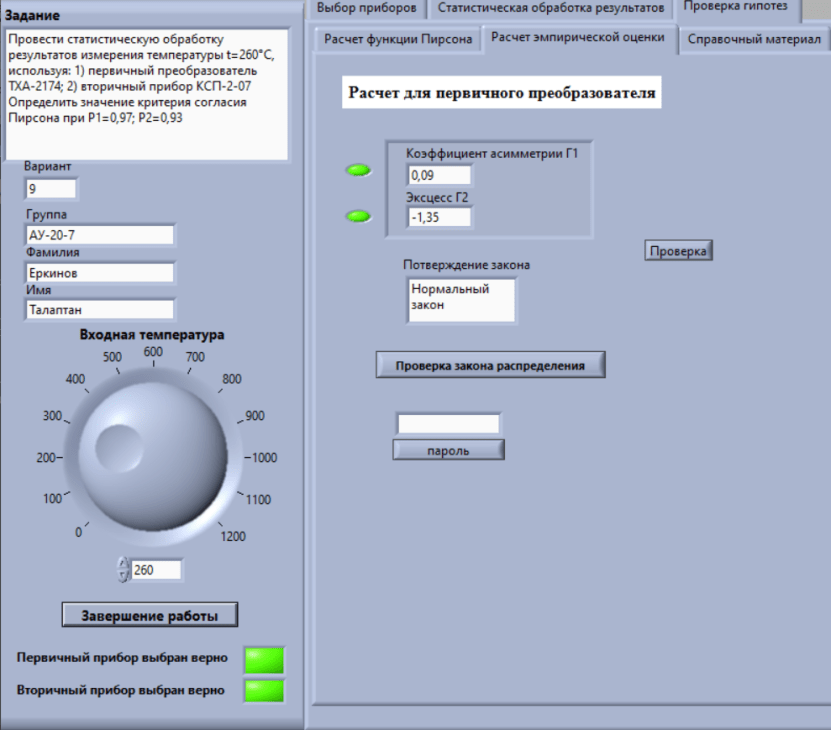 Рисунок 5. Расчет эмпирической оценки для первичного преобразователя. Исключение грубых погрешностей и промахов Производим расчеты грубых погрешностей по правилу «трех сигм» и с помощью статистики, называемой функцией наблюдений v. а) по функции наблюдения v Существует более квалифицированный критерий, согласно которому проверяется гипотеза о том, что сомнительный результат наблюдения Х не содержит грубой погрешности. Сомнительными в первую очередь являются наибольший или наименьший из результатов наблюдений. Поэтому для проверки гипотезы пользуются статистикой, называемой функцией наблюдений, 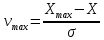 =1,68 или =1,68 или  = 1,92 = 1,92Грубых погрешностей нет, если одновременно выполняются соотношения: 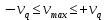 и и 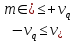 , , где 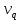 = 2,8474 при Р=0,97 . = 2,8474 при Р=0,97 .-2,8474 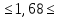 2,8474 и -2,8474 2,8474 и -2,8474 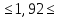 2,8474; 2,8474;б) по правилу «трех сигм» Ip=( 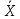 -3σн; -3σн; 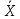 +3σн); Ip= (10,07 ; 10,94) мВ. +3σн); Ip= (10,07 ; 10,94) мВ.Вычисление погрешности измерения При Р=0,97 К=2,2 Погрешность результата наблюдений: 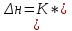  = 2,2*0,14=0,308 мВ = 2,2*0,14=0,308 мВПогрешность результата измерений: 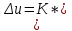 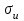 = 2,2*0,028 =0,0616 мВ = 2,2*0,028 =0,0616 мВПредставление результата измерения 1)Результат наблюдений: Х=(x± 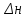 )=(10,5064 ± 0,308) мВ, P=0,97; )=(10,5064 ± 0,308) мВ, P=0,97;2)Результат измерений: Х=(x± 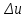 )= (10,5064 ± 0,0616) мВ, P=0,97; )= (10,5064 ± 0,0616) мВ, P=0,97;Результаты после округления: 1)Результат наблюдений: Х=(x± 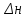 )=(10,5±0,3) мВ, P=0,97; )=(10,5±0,3) мВ, P=0,97;2)Результат измерений: Х=(x± 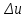 )= (10,5±0,61) мВ, P=0,97. )= (10,5±0,61) мВ, P=0,97.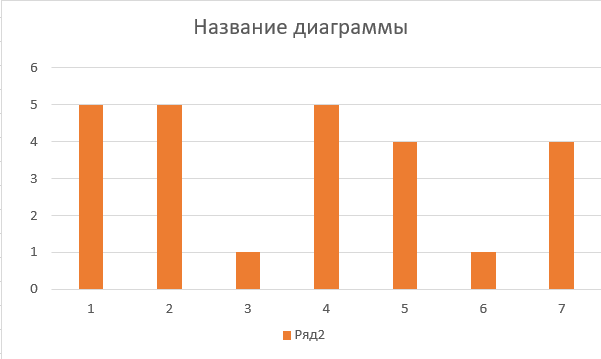 Рисунок 6. Гистограмма. Вторичный прибор Первичный прибор по заданию – КСП-2-07. 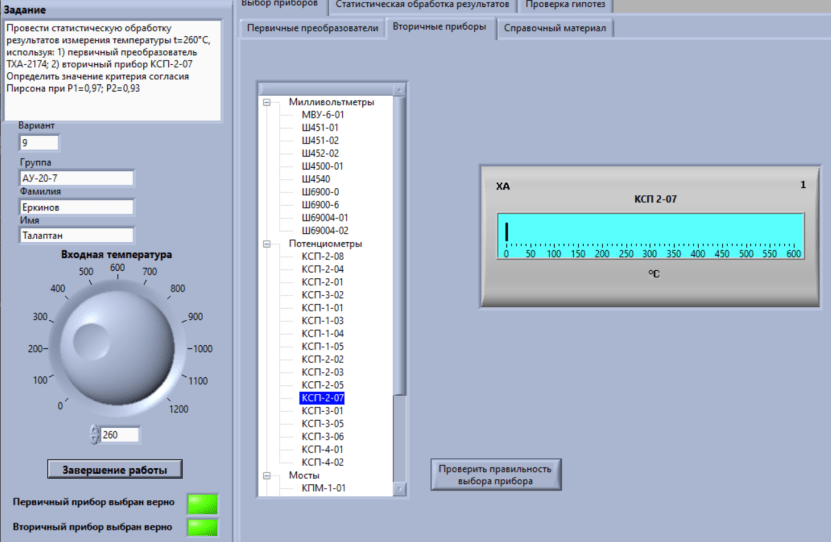 Рисунок 7. Выбор вторичного прибора. После выбора прибора, нужно провести имитационный эксперимент на 25 случайных величин. 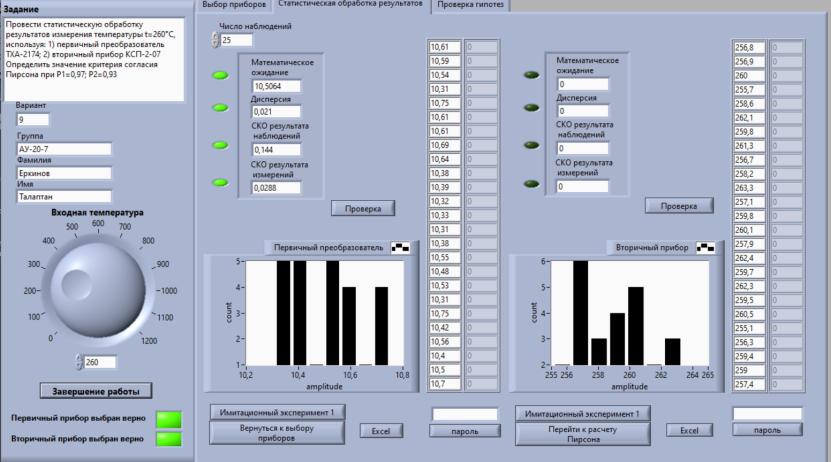 Рисунок 8. Получение 25 случайных величин. Далее, нужно провести статистический расчет полученных результатов, вычисления проводят в таблице Excel. 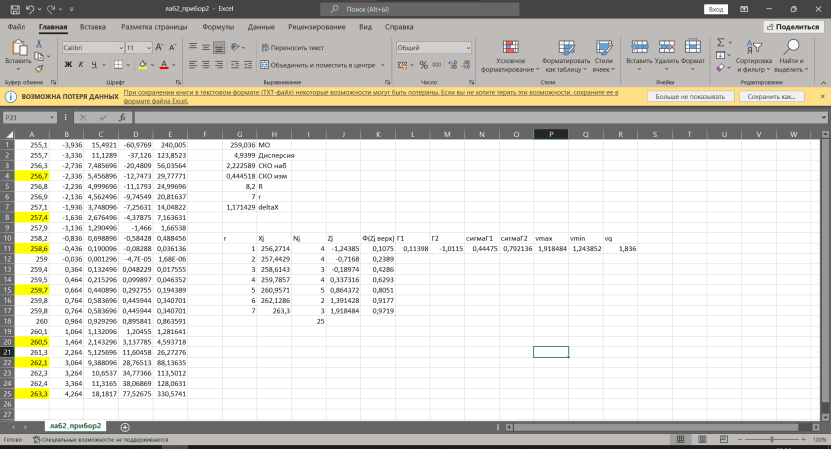 Рисунок 9. Расчет статистических результатов для вторичного прибора. 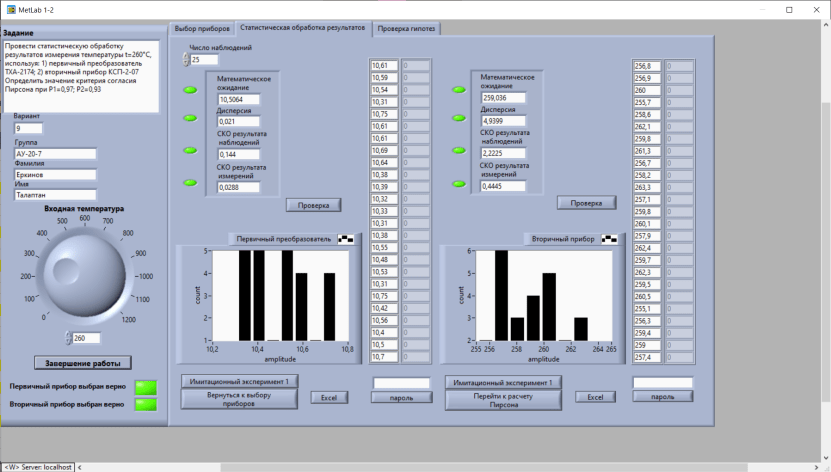 Рисунок 10. Проверка проведенных расчетов. Расчеты для первичного преобразователя а) Математическое ожидание: X = 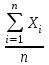 = 259 °С; = 259 °С;б) Дисперсия: D = S2 = 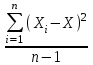 = 4,94 °С; = 4,94 °С;в) Среднеквадратическое отклонение наблюдения: 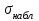 = =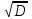 = 2,22 °С; = 2,22 °С;г) Среднеквадратическое отклонение измерения: 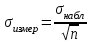 =0,44 °С; =0,44 °С;Проверка гипотезы о нормальном законе распределения по эмпирическим оценкам. Производим расчеты коэффициентов асимметрии и эксцесса для первичного преобразователя. Эмпирическая оценка Г1 коэффициента асимметрии: Г1= 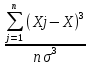 = 0,11 = 0,11Эмпирическая оценка Г2 коэффициента эксцесса: Г2= 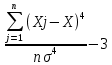 = -1 = -1Степень рассеяния для величин Г1 и Г2 может быть приближенно оценена путем сравнения их с оценкой среднего квадратического отклонения коэффициентов асимметрии 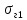 и эксцесса и эксцесса 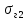 : :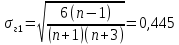 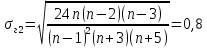 Распределение считают нормальным, если одновременно выполняются соотношения: 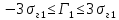 и и 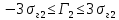 . .Для первичного преобразователя соотношения выполняются, т.е.: -1,335≤ 0,11≤2,376 для коэффициента асимметрии; -2,4≤-1≤2,4 для коэффициента эксцесса, следовательно закон распределения равномерный.  Рисунок 11. Расчет эмпирической оценки для первичного преобразователя. Исключение грубых погрешностей и промахов Производим расчеты грубых погрешностей по правилу «трех сигм» и с помощью статистики, называемой функцией наблюдений v. а) по функции наблюдения v Существует более квалифицированный критерий, согласно которому проверяется гипотеза о том, что сомнительный результат наблюдения Х не содержит грубой погрешности. Сомнительными в первую очередь являются наибольший или наименьший из результатов наблюдений. Поэтому для проверки гипотезы пользуются статистикой, называемой функцией наблюдений, 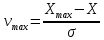 =1,92 или =1,92 или  = 1,24 = 1,24Грубых погрешностей нет, если одновременно выполняются соотношения: 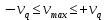 и и 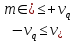 , , где 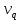 = 1,8 при Р=0,93. = 1,8 при Р=0,93.-1,8 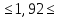 1,8 и -1,8 1,8 и -1,8 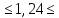 1,8; 1,8;В этом случае, мы имеем грубые погрешности, так как 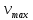 , не входит в диапазон , не входит в диапазон 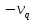 и и 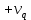 . .б) по правилу «трех сигм» Ip=( 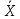 -3σн; -3σн; 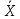 +3σн); Ip= (252,376; 265,696) °С. +3σн); Ip= (252,376; 265,696) °С.Вычисление погрешности измерения При Р=0,93 К=1,8 Погрешность результата наблюдений: 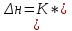 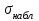 = 1,8*2,22 = 3,996 °С = 1,8*2,22 = 3,996 °СПогрешность результата измерений: 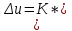 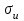 = 1,8*0,45 = 0,81 °С = 1,8*0,45 = 0,81 °СПредставление результата измерения 1)Результат наблюдений: Х=(x± 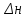 )=(259,036 ± 3,996) °С, P=0,93; )=(259,036 ± 3,996) °С, P=0,93;2)Результат измерений: Х=(x± 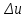 )= (259,036 ± 0,81) °С, P=0,93; )= (259,036 ± 0,81) °С, P=0,93;Результаты после округления: 1)Результат наблюдений: Х=(x± 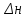 )=(259±4) °С, P=0,93; )=(259±4) °С, P=0,93;2)Результат измерений: Х=(x± 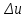 )= (259 ±0,8) °С, P=0,93. )= (259 ±0,8) °С, P=0,93.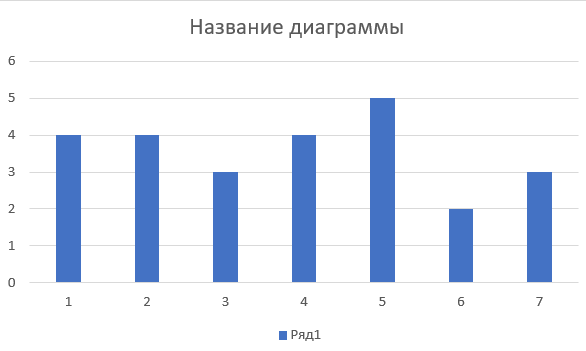 Рисунок 12. Гистограмма. Вывод В ходе выполнения лабораторной работы получили навыки по стандартной обработке результатов многократных измерений при грубых погрешностях и определению законов распределения погрешностей средств измерений, оцениванию погрешностей и представлению результатов измерений. Для данной лабораторной работы были рассчитаны математическое ожидание, дисперсия, среднеквадратичное отклонение изменений, среднеквадратичное отклонение наблюдений. Таким образом, построив гистограмму случайных выборок и числа попаданий в интервал этих выборок, графически подтвердился равномерный закон распределения. Полученные данные по первичному преобразователю: Математическое ожидание= 10,5 мВ; Дисперсия: = 0,021 мВ; Среднеквадратическое отклонение наблюдения: = 0,14 мВ; Среднеквадратическое отклонение измерения: = 0,028 мВ. Построил гистограмму, по виду гистограммы предположил равномерный закон распределения. Произвел расчеты коэффициентов асимметрии и эксцесса для первичного преобразователя. Эмпирическая оценка Г1 коэффициента асимметрии: Г1= 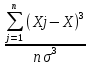 = 0,09 = 0,09Эмпирическая оценка Г2 коэффициента эксцесса: Г2= 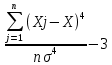 = -1,35 = -1,35Степень рассеяния для величин Г1 и Г2 может быть приближенно оценена путем сравнения их с оценкой среднего квадратического отклонения коэффициентов асимметрии 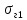 и эксцесса и эксцесса 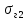 : :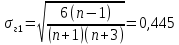 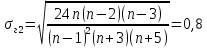 Т.к. выполняются условия: --1,335≤ 0,09≤2,376 для коэффициента асимметрии; -2,4≤-1,35≤2,4 для коэффициента эксцесса, следовательно закон распределения нормальный. Произвел расчеты грубых погрешностей по правилу «трех сигм» и с помощью статистики, называемой функцией наблюдений v. а) по функции наблюдения v Грубых погрешностей нет, если одновременно выполняются соотношения: 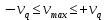 и и 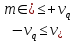 , , где 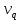 = 2,8474 при Р=0,97 . = 2,8474 при Р=0,97 .-2,8474 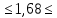 2,8474 и -2,8474 2,8474 и -2,8474  2,8474; 2,8474;б) по правилу «трех сигм» Ip=( 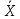 -3σн; -3σн; 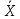 +3σн); Ip= (10,07 ; 10,94) мВ. +3σн); Ip= (10,07 ; 10,94) мВ.Вычисление погрешности измерения При Р=0,97 К=2,2 Погрешность результата наблюдений: 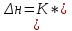  = 2,2*0,14=0,308 мВ = 2,2*0,14=0,308 мВПогрешность результата измерений: 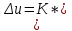  = 2,2*0,028 =0,0616 мВ = 2,2*0,028 =0,0616 мВПредставление результата измерения 1)Результат наблюдений: Х=(x± 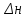 )=(10,5064 ± 0,308) мВ, P=0,97; )=(10,5064 ± 0,308) мВ, P=0,97;2)Результат измерений: Х=(x± 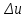 )= (10,5064 ± 0,0616) мВ, P=0,97; )= (10,5064 ± 0,0616) мВ, P=0,97;Результаты после округления: 1)Результат наблюдений: Х=(x± 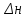 )=(10,5±0,3) мВ, P=0,97; )=(10,5±0,3) мВ, P=0,97;2)Результат измерений: Х=(x± 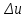 )= (10,5±0,61) мВ, P=0,97. )= (10,5±0,61) мВ, P=0,97.Полученные данные по вторичному прибору: Математическое ожидание = 259 °С; Дисперсия = 4,94 °С; Среднеквадратическое отклонение наблюдения = 2,22 °С; Среднеквадратическое отклонение измерения = 0,44 °С. Построил гистограмму, по виду гистограммы предположил равномерный закон распределения. Произвел расчеты коэффициентов асимметрии и эксцесса для первичного преобразователя. Эмпирическая оценка Г1 коэффициента асимметрии: Г1= 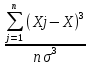 = 0,11 = 0,11Эмпирическая оценка Г2 коэффициента эксцесса: Г2= 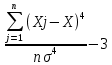 = -1 = -1Степень рассеяния для величин Г1 и Г2 может быть приближенно оценена путем сравнения их с оценкой среднего квадратического отклонения коэффициентов асимметрии 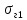 и эксцесса и эксцесса 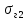 : :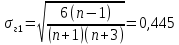 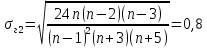 Распределение считают нормальным, если одновременно выполняются соотношения: 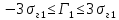 и и 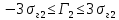 . .Для первичного преобразователя соотношения выполняются, т.е.: -1,335≤ 0,11≤2,376 для коэффициента асимметрии; -2,4≤-1≤2,4 для коэффициента эксцесса, следовательно закон распределения равномерный. Произвел расчеты грубых погрешностей по правилу «трех сигм» и с помощью статистики, называемой функцией наблюдений v. а) по функции наблюдения v Грубых погрешностей нет, если одновременно выполняются соотношения: 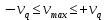 и и 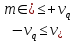 , , где 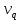 = 1,8 при Р=0,93. = 1,8 при Р=0,93.-1,8  1,8 и -1,8 1,8 и -1,8 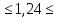 1,8; 1,8;В этом случае, мы имеем грубые погрешности, так как 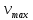 , не входит в диапазон , не входит в диапазон 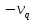 и и 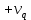 . .б) по правилу «трех сигм» Ip = ( 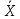 -3σн; -3σн; 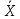 +3σн); Ip= (252,376; 265,696) °С. +3σн); Ip= (252,376; 265,696) °С.Вычисление погрешности измерения При Р=0,93 К=1,8 Погрешность результата наблюдений: 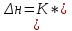 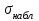 = 1,8*2,22 = 3,996 °С = 1,8*2,22 = 3,996 °СПогрешность результата измерений: 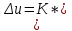 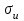 = 1,8*0,45 = 0,81 °С = 1,8*0,45 = 0,81 °СПредставление результата измерения 1)Результат наблюдений: Х=(x± 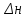 )=(259,036 ± 3,996) °С, P=0,93; )=(259,036 ± 3,996) °С, P=0,93;2)Результат измерений: Х=(x± 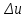 )= (259,036 ± 0,81) °С, P=0,93; )= (259,036 ± 0,81) °С, P=0,93;Результаты после округления: 1)Результат наблюдений: Х=(x± 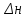 )=(259±4) °С, P=0,93; )=(259±4) °С, P=0,93;2)Результат измерений: Х=(x± 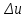 )= (259 ±0,8) °С, P=0,93. )= (259 ±0,8) °С, P=0,93. |
