ОТЧЕТ_4. Отчет По лабораторной работе 4. 1 По курсу Вычислительная математика
 Скачать 342.59 Kb. Скачать 342.59 Kb.
|
|
Федеральное агентство по образованию ФГАОУ ВО «Санкт-Петербургский политехнический университет Петра Великого» Институт компьютерных наук и технологий Кафедра Высшая школа киберфизических систем и управления Отчет По лабораторной работе №4.1 По курсу «Вычислительная математика» по теме «Метод наименьших квадратов» Выполнил студент группы 23533/2 Мусалимов Э.Ш. _____ Проверил Ерофеев С.А. _____ Санкт-Петербург 2018 г. Задание: Дана функция 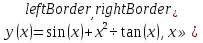 . Необходимо записать в текстовый файл координаты точек, вычисленные с помощью данной функции. Перед аппроксимацией координаты точек записать в массив. Построить график аппроксимирующей функции полинома методом наименьших квадратов на отрезке [ . Необходимо записать в текстовый файл координаты точек, вычисленные с помощью данной функции. Перед аппроксимацией координаты точек записать в массив. Построить график аппроксимирующей функции полинома методом наименьших квадратов на отрезке [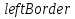 , ,  ]. Интервал [ ]. Интервал [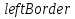 , ,  ], шаг функции и степень полинома задаются пользователем. ], шаг функции и степень полинома задаются пользователем.Теоретические данные: Суть метода наименьших квадратов (МНК).Общий смысл оценивания по методу наименьших квадратов заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. По методу МНК наилучшими коэффициентами  , , 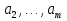 считаются те, для которых сумма квадратов отклонений будет минимальной. считаются те, для которых сумма квадратов отклонений будет минимальной.Отсюда, используя условия экстремума функции нескольких переменных, получаем нормальную систему для определения коэффициентов 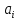 (i = 0, 1, 2,… m): (i = 0, 1, 2,… m):Если система (4) имеет единственное решение, то оно будет искомым. Система (4) упрощается, если эмпирическая функция  , , 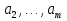 ) является линейной относительно параметров ) является линейной относительно параметров  , , 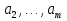 . Действительно, полагая . Действительно, полагаяполучим Отсюда 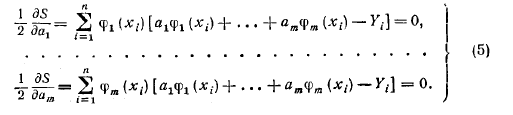 Введем сокращенные обозначения  Систему (5) можно записать в виде нормальной системы 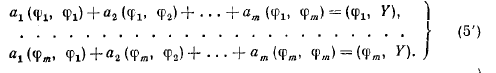 В частном случае, если эмпирическая функция является полиномом y =  , тогда , тогда 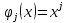 (j = 0, 1, … m) (j = 0, 1, … m)получаем Отсюда нормальная система (5’) будет иметь вид  Метод наименьших квадратов обладает тем преимуществом, что если сумма S квадратов отклонений мала, то сами эти отклонения также малы по абсолютной величине. Метода Гаусса решения СЛАУ Пусть нам требуется решить систему из n линейных алгебраических уравнений с n неизвестными переменными вида, и пусть определитель ее основной матрицы отличен от нуля.  Будем считать, что к n-ому уравнению прибавим первое, умноженное на 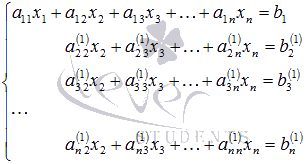 где   . . К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго. Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке  Будем считать, что Для этого к третьему уравнению системы прибавим второе, умноженное на  где  , а , а  Таким образом, переменная x2 исключена из всех уравнений, начиная с третьего. Далее приступаем к исключению неизвестной x3, при этом действуем аналогично с отмеченной на рисунке частью системы  Так продолжаем прямой ход метода Гаусса, пока система не примет вид  С этого момента начинаем обратный ход метода Гаусса: вычисляем xn из последнего уравнения как 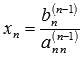 , с помощью полученного значения xn находим xn-1 из предпоследнего уравнения, и так далее, находим x1 из первого уравнения. , с помощью полученного значения xn находим xn-1 из предпоследнего уравнения, и так далее, находим x1 из первого уравнения.Пример работы программы

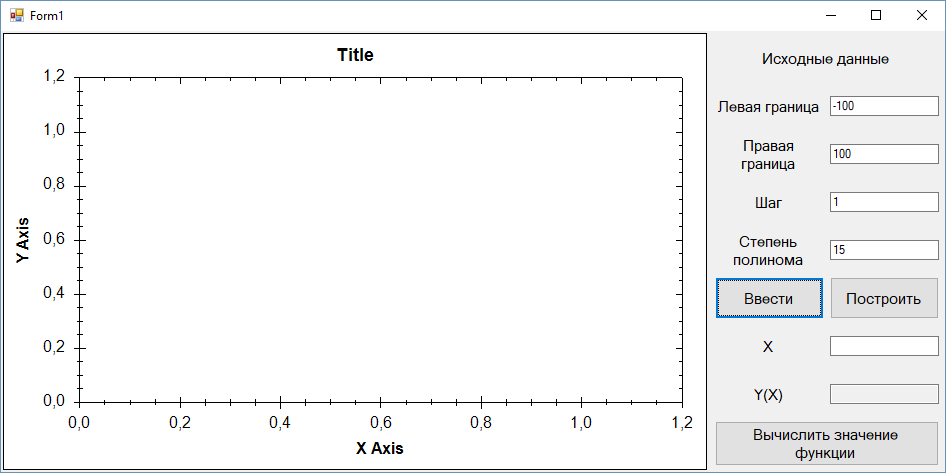

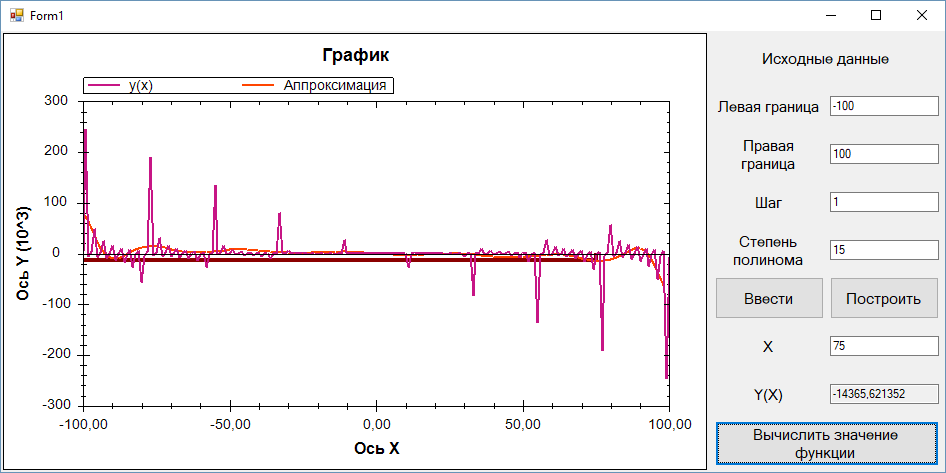 Пример исключительных ситуаций

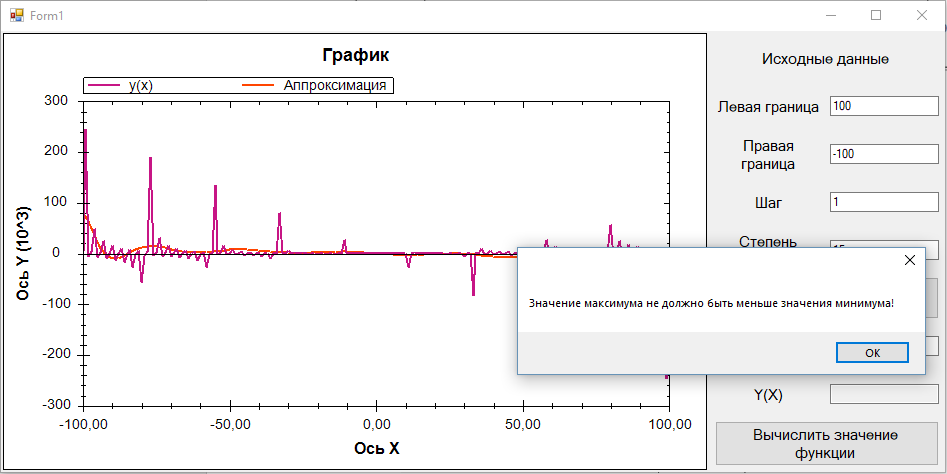

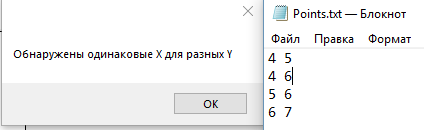


 Вывод При выполнении лабораторной работы нами был изучен метод наименьших квадратов для нахождения функции через решение системы линейных уравнений. Программа вычисляет коэффициенты интерполяционного полинома и строит график среднеквадратичного приближения, который при большой степени многочлена совпадает с большой точностью с графиком исходной функции. Код программы на С# using System; using System.Drawing; using System.Windows.Forms; using System.IO; using ZedGraph; namespace Lab_4_1 { public partial class Form1 : Form { public Form1() { InitializeComponent(); } // Левая граница, Правая граница, Количество точек double rightBorder_ = 0.0, leftBorder_ = 0.0, step_ = 0.0; // Степень полинома int polPower_ = 0; // Точки функции PointPairList list_F = new PointPairList(); // Исходная функция public double calcFun(double x) { return (Math.Sin(x) + x * x * Math.Tan(x)); } LineItem curve1; GraphPane pane; // Вспомогательный массив с коэффициентами double[] coeffArray = null; // Функция построения прямой, A - массив с коэффициентами private double Y(double x, double[] A) { double y = 0.0; for (int i = 0; i < A.Length; i++) y += A[i] * Math.Pow(x, i); return y; } // Найдём коэффициенты многочлена double[] MNK(PointPairList list) { double[] A = new double[polPower_ + 1]; // Матрица коэффициентов многочлена double[,] arr = new double[polPower_ + 1, polPower_ + 2]; // Расширенная матрица for (int i = 0; i < polPower_ + 1; i++) { for (int j = 0; j < polPower_ + 1; j++) { arr[i, j] = 0; for (int z = 0; z < list.Count; z++) arr[i, j] += Math.Pow(list[z].X, i + j); } for (int j = 0; j < list.Count; j++) arr[i, polPower_ + 1] += list[j].Y * Math.Pow(list[j].X, i); } M_Gauss(arr, ref A); return A; } private void M_Gauss(double[,] arr, ref double[] a) { try { int n = a.Length; // Размер несовмещенной матрицы double diag_el = 0.0, x = 0; // Преобразуем матрицу к ступенчатому виду for (int i = 0; i < n; i++) { Max_elem(arr, n, i); diag_el = arr[i, i]; // Преобразуем i-ю строку if (diag_el != 0) for (int j = 0; j < n + 1; j++) arr[i, j] /= diag_el; // Сделаем под элементом главной диагонали i-го столбца нули for (int j = i + 1; j < n; j++) { double temp = arr[j, i]; for (int k = 0; k < n + 1; k++) arr[j, k] -= temp * arr[i, k]; } } // Найдём значения коэффициентов for (int i = n - 1; i >= 0; i--) { // Начальное значение i-ой переменной x = arr[i, n]; // Корректировка начального значения for (int j = i + 1; j < n; j++) x -= a[j] * arr[i, j]; a[i] = x; } } catch (Exception m) { MessageBox.Show(m.Message); } } // Поиск максимального элемента массива в i-м столбeц; arr - совмещенная матрица, n - размер несовмещенной матрицы, i - индекс стобца private void Max_elem(double[,] arr, int n, int i) { int inx_max = i; for (int j = i + 1; j < n; j++) { if (Math.Abs(arr[inx_max, i]) < Math.Abs(arr[j, i])) inx_max = j; } if (inx_max != i) Swap(arr, n, i, inx_max); } // Меняем строки местами. n - размер несовмещенной матрицы, int row1, row2 - номера строк private void Swap(double[,] arr, int n, int row1, int row2) { double temp = 0; for (int i = 0; i < n + 1; i++) { temp = arr[row1, i]; arr[row1, i] = arr[row2, i]; arr[row2, i] = temp; } } private void CreateGraph(ZedGraphControl zgc) { // Зададим панель для графика pane = zgc.GraphPane; zgc.AutoSize = false; pane.XAxis.Scale.MaxAuto = true; pane.XAxis.Scale.MinAuto = true; pane.YAxis.Scale.MaxAuto = true; pane.YAxis.Scale.MinAuto = true; // Установка масштаба pane.XAxis.Scale.Min = leftBorder_; pane.XAxis.Scale.Max = rightBorder_; pane.XAxis.Scale.Format = "F2"; pane.XAxis.Scale.FontSpec.Size = 12; pane.YAxis.Scale.FontSpec.Size = 12; // Очистим список кривых на тот случай, если до этого что-то уже было нарисовано pane.CurveList.Clear(); // Заголовки pane.Title.Text = "График"; pane.XAxis.Title.Text = pane.XAxis.Title.Text = "Ось X"; pane.YAxis.Title.Text = pane.YAxis.Title.Text = "Ось Y"; } private void but_Enter_Click(object sender, EventArgs e) { try { // Вводим и проверяем данные rightBorder_ = double.Parse(tb_RightBorder.Text); leftBorder_ = double.Parse(tb_LeftBorder.Text); step_ = double.Parse(tb_Step.Text); polPower_ = int.Parse(tb_PolPow.Text); if (leftBorder_ > rightBorder_) throw new Exception("Значение максимума не должно быть меньше значения минимума!"); if (rightBorder_ - leftBorder_ < 0.0001) throw new Exception("Значение максимума не должно быть равно минимуму!"); if (step_ > (rightBorder_ - leftBorder_)) throw new Exception("Недопустимо большой шаг функции!"); if (step_ <= 0) throw new Exception("Значение шага функции не может быть меньше, либо равно нулю!"); if ((rightBorder_ - leftBorder_) / (step_) > Math.Pow(10, 4)) throw new Exception("Слишком большое количество точек!"); if (polPower_ > 154 / Math.Log10(rightBorder_)) throw new Exception("Слишком большая степень!"); if ((rightBorder_ - leftBorder_) / (step_) < polPower_ + 1) throw new Exception("Слишком мало точек для данной степени полинома!"); if (polPower_ <= 0) throw new Exception("Недопустимая степень полинома!"); StreamWriter SW = new StreamWriter("Points.txt"); for (double x = leftBorder_; x <= rightBorder_; x += step_) { SW.WriteLine(x + " " + calcFun(x)); } SW.Close(); } catch (Exception mes) { MessageBox.Show(mes.Message); } } private void but_Build_Click(object sender, EventArgs e) { tb_X.Clear(); tb_Y.Clear(); try { list_F.Clear(); pane = zedGraphControl1.GraphPane; pane.CurveList.Clear(); zedGraphControl1.AxisChange(); zedGraphControl1.Invalidate(); //-------------------------------------------------------- // Считываем значение функции из файла StreamReader SR_ = new StreamReader("points.txt"); string rawData = SR_.ReadToEnd(); SR_.Close(); // Записываем данные в массив rdyData string[] rdyData = rawData.Split(' ', '\n', '\r'); // Заполняем массив точек list_F.Clear(); for (int i = 0; i < rdyData.Length - 1; i++) { if (rdyData[i] != "") { Convert.ToDouble(rdyData[i]); } if (rdyData[i] != "" && rdyData[i + 1] != "") { list_F.Add(Convert.ToDouble(rdyData[i]), Convert.ToDouble(rdyData[i + 1])); } } // Проверяем входные данные if (list_F.Count < 2) { throw new Exception("Невозможно построить график по одной точке"); } list_F.Sort(); for (int i = 0; i < list_F.Count - 1; i++) { if (list_F[i].X == list_F[i + 1].X && list_F[i].Y != list_F[i + 1].Y) throw new ApplicationException("Обнаружены одинаковые X для разных Y"); } if (list_F.Count == 1) { throw new Exception("Невозможно построить график по одной точке"); } polPower_ = int.Parse(tb_PolPow.Text); if (polPower_ == 0) { throw new Exception("Выберите степень интерполяции"); } if (polPower_ > list_F.Count) { throw new Exception("Степень интерполяции должна быть мeньше количества точек"); } //------------------------------------------------------------------------- //Проверим границы графика rightBorder_ = list_F[list_F.Count - 1].X; leftBorder_ = list_F[0].X; //------------------------------------------------------------------- CreateGraph(zedGraphControl1); //Строим график Draw(list_F); coeffArray = MNK(list_F); //Построим полученную прямую Draw_line(coeffArray); } catch (FileNotFoundException) { throw new Exception("Возникла ошибка. Файл не найден."); } catch (Exception mes) { MessageBox.Show(mes.Message); } } private void but_Calc_Click(object sender, EventArgs e) { try { double x = double.Parse(tb_X.Text); if (x < leftBorder_ || x > rightBorder_) throw new Exception("Значение Х не входит в введённый интервал!"); double y = Y(x, coeffArray); tb_Y.Text = string.Format("{0:F6}", y); //Строим прямые к найденной точке PointPairList line = new PointPairList(); curve1.Clear(); Draw(list_F); Draw_line(coeffArray); line.Add(0, y); line.Add(x, y); line.Add(x, 0); curve1 = pane.AddCurve("", line, Color.DarkRed, SymbolType.None); curve1.Line.Width = 4; // Вызываем метод AxisChange(), чтобы обновить данные об осях. zedGraphControl1.AxisChange(); // Обновляем график zedGraphControl1.Invalidate(); } catch (Exception mes) { MessageBox.Show(mes.Message); } } private void Draw(PointPairList list) { //Готовим наш массив с точками list.TrimExcess(); list.Sort(); try { pane.CurveList.Clear(); //Подписываем график curve1 = pane.AddCurve("y(x)", list, Color.MediumVioletRed, SymbolType.None); curve1.Line.Width = 2; // Вызываем метод AxisChange(), чтобы обновить данные об осях. zedGraphControl1.AxisChange(); // Обновляем график zedGraphControl1.Invalidate(); } catch (Exception m) { MessageBox.Show(m.Message); } } private void Draw_line(double[] A) { try { PointPairList list = new PointPairList();//Создаём лист с точками //Вычисляем значение прямой for (double x = leftBorder_; x < rightBorder_; x += (rightBorder_ - leftBorder_) / 100) list.Add(x, Y(x, A)); list.Sort(); //Подписываем график curve1 = pane.AddCurve("Аппроксимация", list, Color.OrangeRed, SymbolType.None); curve1.Line.Width = 2; // Вызываем метод AxisChange(), чтобы обновить данные об осях. zedGraphControl1.AxisChange(); // Обновляем график zedGraphControl1.Invalidate(); } catch (Exception m) { MessageBox.Show(m.Message); } } } } |
