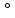4 лабораторная работа, механика. Отчет,л.4 механика. Отчет по лабораторной работе 4 (механика) Измерение скорости полета с помощью балластического маятника
 Скачать 319.27 Kb. Скачать 319.27 Kb.
|
|
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ  МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра общей и технической физики Отчет по лабораторной работе №4 (механика) «Измерение скорости полета с помощью балластического маятника» Выполнил: студент гр. ГС-21-1 Черниговская М.В. (шифр группы) (подпись) (Ф.И.О.) Дата: Проверил: (должность) (подпись) (Ф.И.О.) Цель работы: определить скорость полета пули с помощью крутильных колебаний баллистического маятника. Краткие теоретические сведения а) В основе эксперимента лежит явление неупругого соударения тел, в результате которого баллистический маятник совершает крутильные колебания. б) Определение основных физических понятий и величин Абсолютно неупругий удар-столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое Момент инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс nматериальных точек системы на квадраты их расстояний до рассматриваемой оси Период крутильных колебаний маятника- время, за которое маятник совершает одно колебание в) Если пренебречь силами трения можно воспользоваться законами сохранения. Закон сохранения момента импульса: момент импульса замкнутой системы тел относительно любой неподвижной точки не изменяется с течением времени. L=const Закон сохранения полной механической энергии: если на механическую систему (тело) не действуют неконсервативные силы (силы сопротивления), то механическая энергия системы сохраняется. 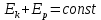 Теорема Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции относительно параллельной оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями. 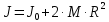 , ,где M – масса одного груза. Зависимость периода крутильных колебаний маятника T от его момента инерции: 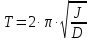 г) пояснения к формулам пункта 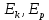 – кинетическая и потенциальная энергии, [Ek]=[Ep]= Дж; – кинетическая и потенциальная энергии, [Ek]=[Ep]= Дж;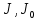 - моменты инерции маятника с грузом и без груза, [J]=[J0]= кг*м2; - моменты инерции маятника с грузом и без груза, [J]=[J0]= кг*м2;D– модуль кручения проволоки. 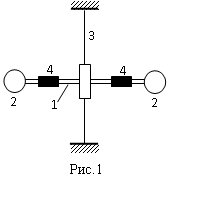 Схема установки Схема установкиБалластический маятник: 1- стержни,2 шт.; 2- емкости с пластилином,2шт.; 3- проволока; 4- грузы; Установка: 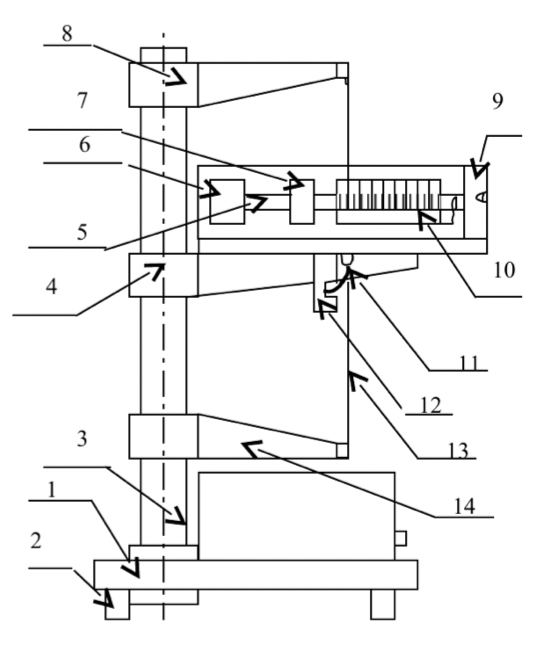 1- основание; 1- основание;2- регулирующиеся ножки; 3- колонка; 4- средний кронштейн; 5- 2 стержня; 6- 2 мисочки; 7- 2 перемещающих груза; 8- верхний кронштейн; 9- стреляющее устройство; 10- угловая шкала; 11- «водилка»; 12- фотоэлектрический датчик; 13- стальная проволока; 14- нижний кронштейн; Основная расчетная формула скорости пули 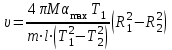 , ,где M,m – массы пули и грузов, [M]=[m]=кг; max- максимальный угол отклонения маятника; T1,T2 -периоды колебания маятника [T1]=[T2]=с; R,l – расстояние от оси вращения маятника до центра масс грузов и до точки удара пули, [R]=[l]=с. 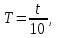 где T – период,[T]=c t – измеренное время, [t]=с. Формула для расчёта погрешности косвенных измерений 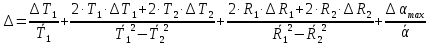
Пример вычислений а) исходные данные M = 0,2 кг m= 0,0125 кг max= 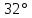 R1 = 0,09 м R2 =0,025 м l = 0,12 м б) погрешности прямых измерений 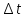 = 0,01 с = 0,01 с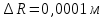 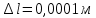  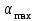 = =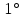  T =0,001с T =0,001с m= m=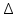 M=1 г M=1 гв) 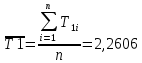 c c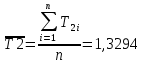 c c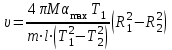 = = 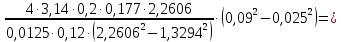 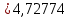 (м/c) (м/c)г) вычисление погрешности косвенных измерений 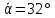 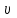 ср = 4,72774 м/с ср = 4,72774 м/с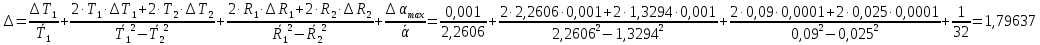 В ходе работы имеем:  = =  ср ± ср ±   = 4,72774 ± 1,79637 (м/с) = 4,72774 ± 1,79637 (м/с)Вывод: данная лабораторная работа позволяет понять принцип работы баллистического маятника, с помощью которого можно найти скорость пули. Малая погрешность говорит о высокой точности приборов. Санкт-Петербург 2022 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||