Отчет по лабораторной работе 5 Линеаризация системы дифференциальных уравнений сау
 Скачать 64.56 Kb. Скачать 64.56 Kb.
|
|
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ТУЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Политехнический институт Кафедра робототехники и автоматизации производства ОТЧЕТПО лабораторной работе №5«Линеаризация системы дифференциальных уравнений САУ» по учебной дисциплине «МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ СИСТЕМ»ВАРИАНТ З-6 Выполнил: ст. гр. 621011 Нгуен.М.Т. Проверил: к.т.н., доцент кафедры ИБ Середин О.С. ‘ ЦЕЛЬ РАБОТЫ Изучение понятия линейного и нелинейного уравнения, условий и способов линеаризации дифференциальных уравнений. ЗАДАНИЕ НА РАБОТУ Привести мотивированное заключение, какие дифференциальные уравнения в составе исходной системы являются линейными, а какие нелинейными; Ввести обозначение номинальных значений переменных и отклонений переменных от номинальных значений (перечень обозначений либо четкое изложение принципа формирования этих обозначений); Сформировать мотивированное заключение, какие переменные системы имеют нулевые номинальные значения; Составить линеаризованную систему уравнений с пояснениями, если линеаризация данного уравнения проводилась способом, отличным от принятого в работе; Для каждого вновь вводимого коэффициента необходимо указать его единицу измерения. 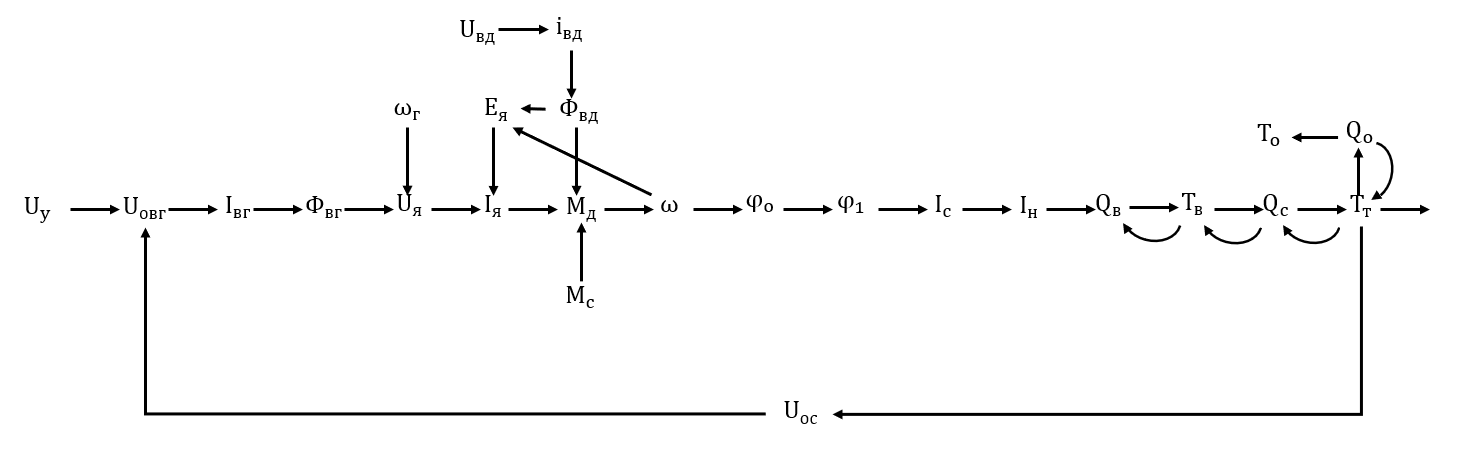 Рисунок 1 – Сигнальный граф Система автоматического регулирования температуры электропечи сопротивления ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Если некоторые уравнения, входящие в систему дифференциальных уравнений САУ, нелинейны, то исследование и решение системы уравнений затрудняются. Поэтому обычно стремятся заменить нелинейные уравнения линейными так, чтобы получаемая при этом система линейных уравнений (линейная модель) приближенно отражала свойства САУ при выполнении некоторых условий. Такую приближенную замену нелинейных уравнений линейными называют линеаризацией системы дифференциальных уравнений. Как правило, САУ предназначена для поддержания некоторого вполне определенного значения управляемой величины. Такое значение называют номинальным. Номинальному значению управляемой величины соответствуют некоторые номинальные значения всех внешних воздействий на систему: сигнала задания и возмущающих воздействий. Если после установления постоянных номинальных значений внешних воздействий прошло достаточно много времени и все переходные процессы в системе закончились, то в системе установился номинальный режим. Номинальному режиму соответствуют некоторые номинальные значения всех внутренних переменных. ХОД РАБОТЫ Произведем линеаризацию системы дифференциальных уравнений из лабораторной работы №4. 1) 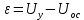 - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: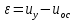 . .2) 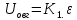 - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: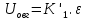 где где 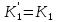 . .3) 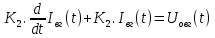 - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: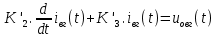 где где 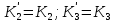 . .4)Зависимость магнитного потока возбуждения генератора от величины тока возбуждения Iвг задана графически. Отметив на графике точку номинального режима и проведя касательную к графику в этой точке, получим линеаризованную зависимость магнитного потока от тока в отклонениях. Тангенс угла наклона к оси iвг обозначим К4. Линеаризованная зависимость примет вид 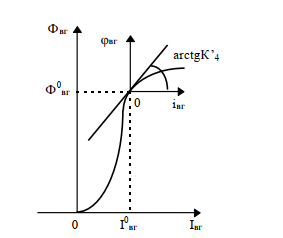 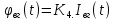 - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: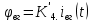 где где 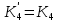 . .5) Для линеаризации зависимости напряжения на щетках якоря генератора Uг от величины магнитного потока возбуждения Фвг и скорости привода генератора г необходимо найти частные производные Uг. по переменным Фвг и вг в точке номинального режима: 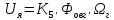 - нелинейное уравнение, поэтому найдем частные производные по всем аргументам: - нелинейное уравнение, поэтому найдем частные производные по всем аргументам: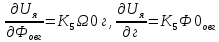 Линеаризованная зависимость: 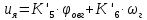 где где  6)  - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: 7)Линеаризация зависимости вращающего момента на валу двигателя Мд от тока якоря Iя и величина потока возбуждения аналогична линеаризации уравнения п. 4. Линеаризованная зависимость: 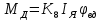 - нелинейное уравнение, поэтому найдем частные производные по всем аргументам: - нелинейное уравнение, поэтому найдем частные производные по всем аргументам: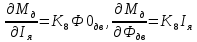 Конечная линеаризованная зависимость: 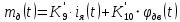 Где 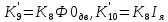 8) 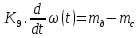 - нелинейное уравнение, поэтому найдем частные производные по всем аргументам - нелинейное уравнение, поэтому найдем частные производные по всем аргументам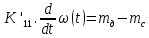 где где 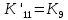 9) 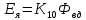 - нелинейное уравнение, поэтому найдем частные производные по всем аргументам - нелинейное уравнение, поэтому найдем частные производные по всем аргументам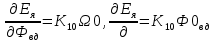 Линеаризованная зависимость: 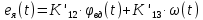 Где 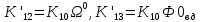 10) 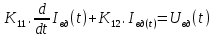 - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: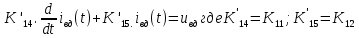 11)Линеаризация графически заданной зависимости величины магнитного потока возбуждения двигателя Фвд от тока возбуждения проводится аналогично 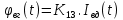 - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: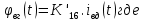 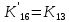 12)  - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: где где  13)  - нелинейное уравнение, из этого получим: - нелинейное уравнение, из этого получим: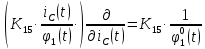 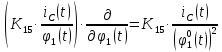 тогда, 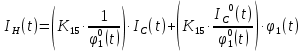 где 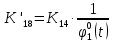 , , 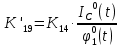 . . В итоге, получим 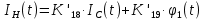 14) 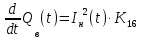 - нелинейное уравнение. - нелинейное уравнение.Выходной величиной является функция 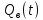 , которая является производной от правой части рассматриваемого уравнения. , которая является производной от правой части рассматриваемого уравнения. Пусть 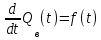 , тогда , тогда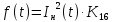 Возьмём частные производные функции 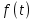 : :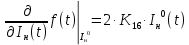 Тогда линеаризованная зависимость примет вид:  где  . .15)  - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: где где  . .16)  - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: где где  . .17)  - линейное уравнение, из этого получим: - линейное уравнение, из этого получим: где где  . . |
