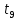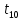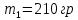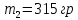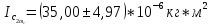Изучение плоскопараллельного движения твердого тела на примере маятника Максвелла.. 7лр. Отчет по лабораторной работе 7 Изучение плоскопараллельного движения твердого тела на примере маятника Максвелла
 Скачать 33.85 Kb. Скачать 33.85 Kb.
|
|
Национальный Исследовательский Ядерный Университет МИФИ Институт Атомной Энергетики Кафедра Общей и Специальной Физики Отчет по лабораторной работе №7: Изучение плоскопараллельного движения твердого тела на примере маятника Максвелла. Студент: Бахтин Я.В. Группа: ИВТ-Б21 Обнинск 2021г. ЦЕЛЬ РАБОТЫ: Изучить плоскопараллельное движение твердого тела, то есть такого движения, при котором все точки тела описывают траектории, лежащие в параллельных плоскостях. Вычислить момент инерции маятника по экспериментальным результатам и оценить его абсолютную и относительную погрешности. Вычислить момент инерции и оценить погрешность. КРАТКАЯ ТЕОРИЯ: Плоскопараллельное движение твердого тела - такое движение, при котором все точки тела описывают траектории, лежащие в параллельных плоскостях. При плоском движении центр масс твердого тела движется в определенной плоскости, неподвижной в лабораторной системе отсчета, а вектор его угловой скорости все время остается перпендикулярным этой плоскости. Уравнение движения центра масс: 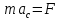 ; (1) ; (1)Уравнением вращательного движения, которое для случая вращения вокруг оси симметрии тела, проходящей через центр масс, и, следовательно, совпадающей с одной из главных осей инерции тела, имеет вид 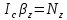 , (2) , (2)где m - масса тела; F - сумма сил, действующих на тело; βz - угловое ускорение тела, 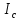 - момент инерции тела относительно оси, проходящей через центр масс, - момент инерции тела относительно оси, проходящей через центр масс, 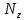 - сумма проекций моментов сил, действующих на тело, на ось вращения - сумма проекций моментов сил, действующих на тело, на ось вращенияЗаписывая моменты сил натяжения нитей в явном виде, можно переписать уравнение (2) как: 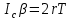 , (3) , (3)где Т-модуль силы натяжения нити. 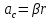 ; (4) ; (4)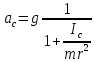 ; (5) ; (5)Величина ускорения ac определяется экспериментально по прямым измерениям времени опускания маятника t проходимому при этом расстояние S. Так как маятник начинает движение из состояния покоя и движется под действием постоянных сил, то: 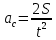 (6) (6)Подстановка ускорения из этого уравнения в предыдущее дает значение момента инерции: 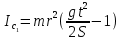 ; (7) ; (7)Момент инерции маятника 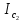 можно представить как сумму моментов трех его частей: момента инерции маятника можно представить как сумму моментов трех его частей: момента инерции маятника 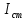 , момента инерции диска , момента инерции диска 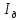 с отверстием для стержня и момента инерции сменного кольца с отверстием для стержня и момента инерции сменного кольца 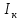 , надеваемого на диск: , надеваемого на диск: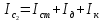 ; (7) ; (7)Момент инерции стержня относительно оси вращения, проходящей через его концы, определяется как 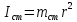 , (8) , (8)где 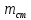 - масса стержня, r - его радиус. - масса стержня, r - его радиус.Момент инерции диска, вращающегося вокруг оси, перпендикулярной диску и проходящей через его центр, записывается следующим образом: 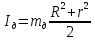 , (9) , (9)где 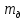 - масса диска, R - его внешний радиус, r - внутренний радиус. - масса диска, R - его внешний радиус, r - внутренний радиус.Момент инерции кольца рассчитывается аналогичным образом: 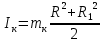 , (10) , (10)где 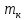 - масса кольца, - масса кольца, 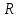 - внутренний радиус кольца, - внутренний радиус кольца, 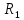 - внешний радиус кольца. - внешний радиус кольца.ХОД РАБОТЫ:
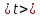 = =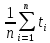 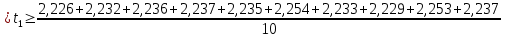 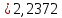 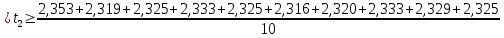 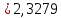 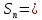 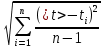 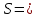 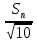 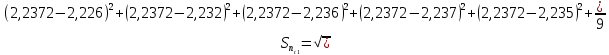 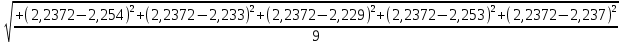 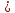 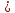 0,0092832 0,0092832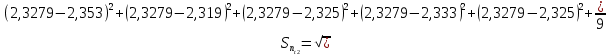 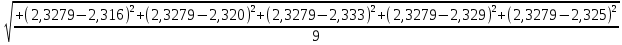   0,0104971 0,0104971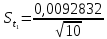 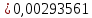 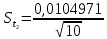 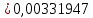 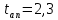 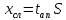 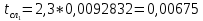 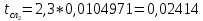 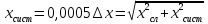 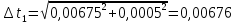 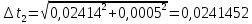 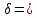 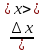 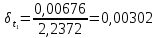 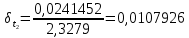 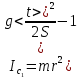 , где , где 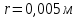 , ,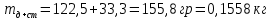 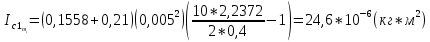 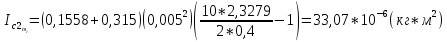 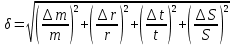 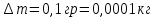 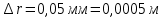 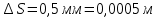 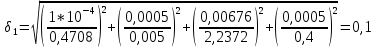 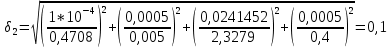 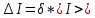 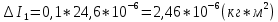 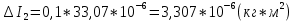 ИТОГ: 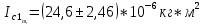 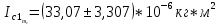 Вычисление момента инерции 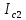 по расчетным данным: по расчетным данным: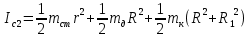 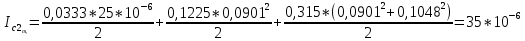 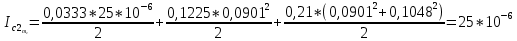 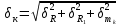 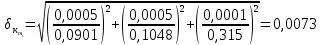 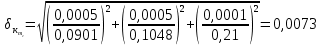 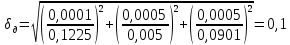 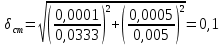 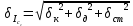 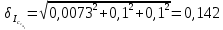 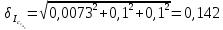 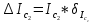 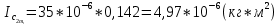 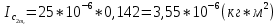 ИТОГ: 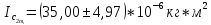 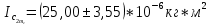 ВЫВОД: Экспериментально, с помощью маятника Максвелла мы изучили плоскопараллельное движение тела. Сопоставили значения моментов инерции маятника Максвелла. Сопоставили значения моментов инерции маятника ( 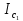 ) по экспериментальным результатам со значениями моментов инерции маятника ( ) по экспериментальным результатам со значениями моментов инерции маятника (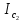 ), они получились примерно одинаковыми, теперь мы можем привести таблицу: ), они получились примерно одинаковыми, теперь мы можем привести таблицу:
|