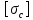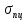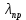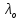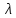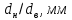Отчет по лабораторной работе 9 Расчет буровых вышек башенного типа Выполнил студент группы ндб 19 Принял
 Скачать 479.82 Kb. Скачать 479.82 Kb.
|
|
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра нефтегазового дела Бурение скважин на шельфе Отчет по лабораторной работе № 9 Расчет буровых вышек башенного типа Выполнил студент группы НДб 19 Принял Иркутск 2022 Лабораторная работа 9.Расчет буровых вышек башенного типаЦель работы: рассчитать нагрузки на вышку башенного типа и сделать проверочный расчет на устойчивость ноги в нижней ее части. Краткие теоретические сведения.На буровые вышки (мачты) действуют различные по силе и величине нагрузки, которые можно разделить на вертикальные и горизонтальные. Расчет производим без учета горизонтальных нагрузок. К вертикальным нагрузкам относятся: нагрузка на крюке, определяемая наибольшим весом спускаемой в скважину колонны; собственная масса вышки (мачты), натяжение ходового и неподвижного (мертвого) концов каната; вертикальные составляющие от натяжения в растяжках.Силы, действующие вдоль ног вышки, уравновешиваются реакциями фундаментных опор, а горизонтальные силы самоуравновешены. В результате этого, если боковые грани вышки представляют собой статически определенные фермы, то напряженными от действия нагрузки на кронблок будут ноги вышки и ее верхнее основание (подкранблочная рама), а пояса и раскосы не испытывают усилий. Вес колонны бурильных или обсадных труб Q, спускаемых в скважины, может быть определен по формуле Для колонны бурильных труб 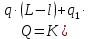 l]. (1) l]. (1)Знак минус показывает, что при спуске нагрузка на крюк будет меньше осевой силы тяжести на величину сил сопротивления. Применяется в вертикальных и наклонных скважинах. Для колонны обсадных труб 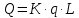 , (2) , (2)где q, 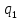 – соответственно вес 1м бурильных труб и 1м УБТ, Н; L – длина колонны бурильных труб, м;l– длина УТБ, м; K – коэффициент, учитывающий потерю веса труб в промывочной жидкости, – соответственно вес 1м бурильных труб и 1м УБТ, Н; L – длина колонны бурильных труб, м;l– длина УТБ, м; K – коэффициент, учитывающий потерю веса труб в промывочной жидкости,K=1-( 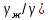 , (3) , (3)где ( 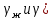 - соответственно плотность промывочной жидкости и материала бурильных труб, кг/ - соответственно плотность промывочной жидкости и материала бурильных труб, кг/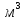 . .При более точных расчетах вес инструмента равен 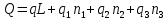 , (4) , (4)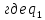 – вес одной муфты, Н; n1 - количество муфт; q2–вес одного замка, Н; – вес одной муфты, Н; n1 - количество муфт; q2–вес одного замка, Н;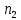 -количество замков; -количество замков;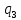 - увеличение веса трубы за счет высаженных концов, Н; - увеличение веса трубы за счет высаженных концов, Н; 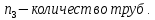 Нагрузка на крюк 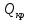 будет больше веса инструмента вследствие прихватов труб в скважине, динамических нагрузок при расхаживании инструмента и сил сопротивления при подъеме о стенки скважины: будет больше веса инструмента вследствие прихватов труб в скважине, динамических нагрузок при расхаживании инструмента и сил сопротивления при подъеме о стенки скважины: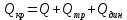 , (5) , (5)Сила трения при подъеме бурильных труб обычно принимается равной 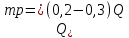 . .Динамические нагрузки возникают в начале подъема свечи в период разгона 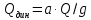 (6) (6)где g - ускорение силы тяжести, м/ 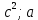 – ускорение движения колонны, м/ – ускорение движения колонны, м/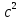 . .Ускорение движения колонны определяется по формуле 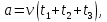 (7) (7)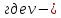 скорость подъема бурильных труб, м/с; скорость подъема бурильных труб, м/с; 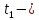 период разгона при подъеме (для геологоразведочного бурения период разгона при подъеме (для геологоразведочного бурения 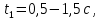 для нефтяного бурения для нефтяного бурения 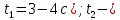 установившейся подъем, с; установившейся подъем, с; 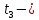 период остановки (0,2 – 0,5), с. период остановки (0,2 – 0,5), с.При бурении наклонных скважин нагрузка на крюке равна (рис.1) 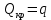 ∙L∙(l ∙L∙(l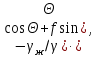 (8) (8)где 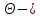 угол наклона скважины от вертикали (зенитный угол),град; угол наклона скважины от вертикали (зенитный угол),град; 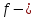 коэффициент трения стали о горную породу или обсадныетрубы (при трении по горным породам коэффициент трения стали о горную породу или обсадныетрубы (при трении по горным породам 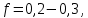 а по обсадным трубам а по обсадным трубам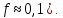 Общая нагрузка на кронблок буровой вышки от действия вертикальныхопределяется по формуле 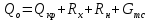 (9) (9)где 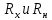 - соответственно усилия в ходовом (подвижном) и неподвижном (мертвом) концах каната, Н; - соответственно усилия в ходовом (подвижном) и неподвижном (мертвом) концах каната, Н; 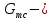 вес талевой системы, Н. вес талевой системы, Н.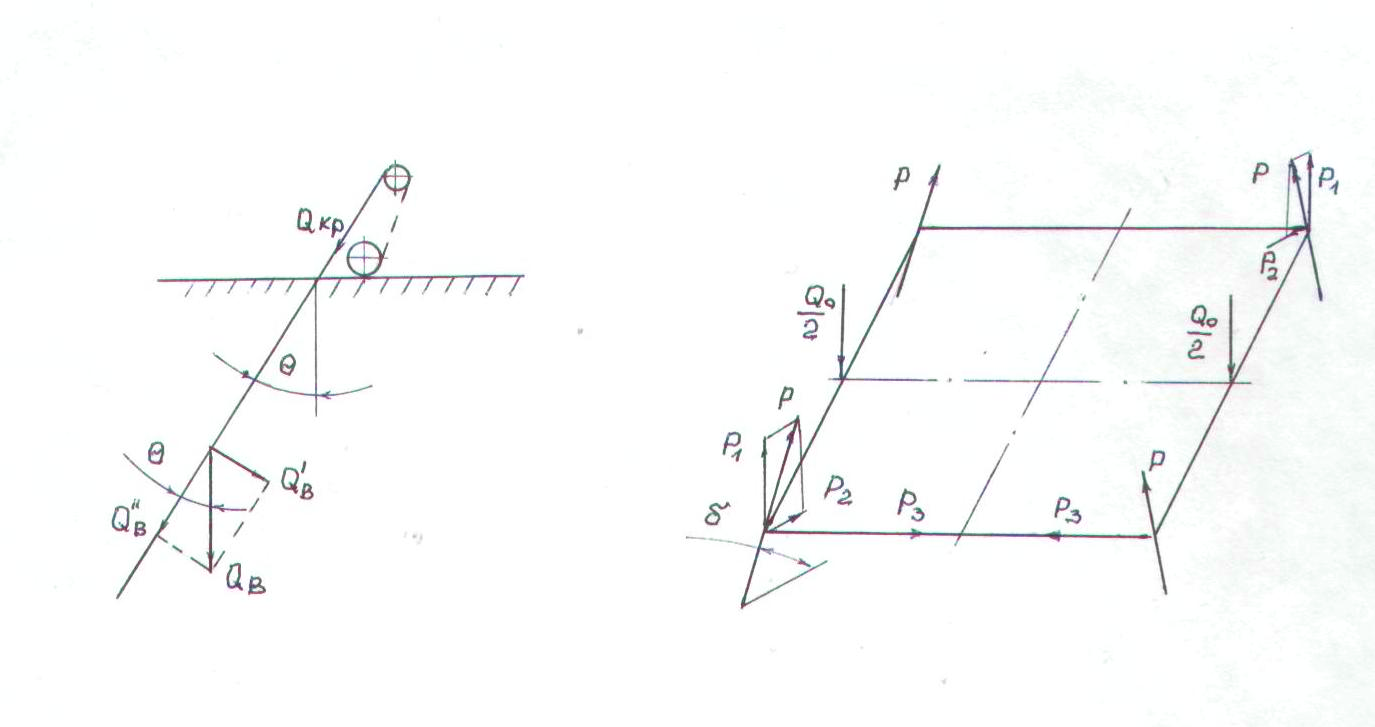
Нагрузку на кронблок вышки можно считать приложенной в центре кронблочной рамы, и тогда вертикальные составляющие реакций в узлах верхнего основания (рис.2) будут одинаковыми и при оснастке с мертвым концом каната 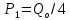 (10) (10)Вдоль оси ноги будет действовать сила 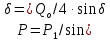 , (11) , (11)где 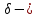 угол между ногой вышки и горизонтальной плоскостью, град. угол между ногой вышки и горизонтальной плоскостью, град. В плоскости верхней рамы по диагонали будут действовать силы 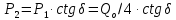 , (12) , (12)и по каждому из стержней силы 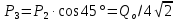 · ·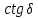 (13) (13)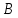 нижней части ноги четырехногой буровой вышки будет действовать нагрузка нижней части ноги четырехногой буровой вышки будет действовать нагрузка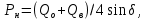 (14) (14)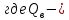 вес вышки. вес вышки.Нагрузка 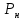 принимается за расчетную. Приближенно ноги вышки рассчитывают на продольный изгиб в зависимости от гибкости по формулам Эйлера, Тетмайера-Ясинского или на прочность. Расчет проводится на участке между первым поясом и основанием, где на ноги действует как полезная нагрузка, так и масса буровой вышки, а длина этого участка ног обычно больше остальных. принимается за расчетную. Приближенно ноги вышки рассчитывают на продольный изгиб в зависимости от гибкости по формулам Эйлера, Тетмайера-Ясинского или на прочность. Расчет проводится на участке между первым поясом и основанием, где на ноги действует как полезная нагрузка, так и масса буровой вышки, а длина этого участка ног обычно больше остальных. Для предотвращения продольного изгиба необходимо выполнить условие 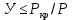 , (15) , (15)где 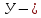 коэффициент запаса устойчивости ног буровой вышки (для стали 1,5 – 2 , для дерева коэффициент запаса устойчивости ног буровой вышки (для стали 1,5 – 2 , для дерева 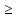 2); 2); 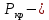 критическая сила, Н; критическая сила, Н;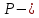 сила, сжимающая стержень, Н. сила, сжимающая стержень, Н.Формула Эйлера для определения критической силы, действующей на стержень, имеет вид 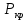 = =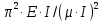 (16) (16)где 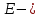 модуль продольной упругости материала стержня, Па; модуль продольной упругости материала стержня, Па; 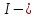 наименьший экваториальный момент инерции поперечного сечения стойки, наименьший экваториальный момент инерции поперечного сечения стойки, 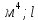 −длина расчетного участка ноги, м; −длина расчетного участка ноги, м;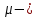 коэффициент, зависящий от типа и расположения опор и характера нагрузки (при шарнирном закреплении концов стойки, что наиболее характерно для условий буровой вышки, он равен (0,725 коэффициент, зависящий от типа и расположения опор и характера нагрузки (при шарнирном закреплении концов стойки, что наиболее характерно для условий буровой вышки, он равен (0,725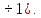 Нормальное критическое напряжение, возникающее в поперечном сечении стержня при 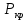 , определяется по формуле , определяется по формуле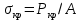 или или 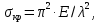 (17) (17)где 𝜆 - гибкость стержня, равная 𝜇∙l /i;А - площадь поперечного сечения ноги вышки. Минимальный радиус инерции поперечного сечения стойки определяется из соотношения i= 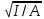 , (18) , (18)Формула Эйлера применима лишь в пределах справедливости закона Гука, т.е. при условии, когда критическое напряжение не превышает предела пропорциональности материала стержня 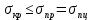 (см. таблицу 1). (см. таблицу 1).Применимость формулы Эйлера может быть установлена из соотношения 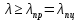 , ,где 𝜆 - гибкость стержня, зависящая от его длины, размеров и формы поперечного сечения (для деревянных конструкций 𝜆 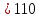 , для стальных 𝜆 , для стальных 𝜆 . .Предельная (граничная) гибкость для материала стержня, зависящая только от физико-механических свойств материала, определяется по формуле 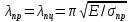 , (19) , (19)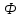 ормула Тетмайера-Ясинского используется для определения напряжений в стержнях при гибкостях меньше предельных. Критические напряжения находят по линейной эмпирической зависимости ормула Тетмайера-Ясинского используется для определения напряжений в стержнях при гибкостях меньше предельных. Критические напряжения находят по линейной эмпирической зависимости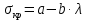 , (20) , (20)тогда 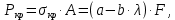 (21) (21) начение коэффициентов начение коэффициентов 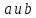 , имеющих размерность напряжения, устанавливаются экспериментально или по таблице 1. , имеющих размерность напряжения, устанавливаются экспериментально или по таблице 1.Формула Тетмайера-Ясинского применима тогда, когда гибкость стержня находится в пределах 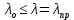 (22) (22)где 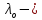 то значение гибкости, при котором критическое напряжение равно предельному (опасному) при сжатии. то значение гибкости, при котором критическое напряжение равно предельному (опасному) при сжатии.Следовательно, стержни, находящиеся в сжатом состоянии, рассчитывают по трем методикам: Стержни большой гибкости – по формуле Эйлера при 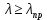 , стержни средней гибкости – по эмпирической формуле Тетмайера-Ясинского при , стержни средней гибкости – по эмпирической формуле Тетмайера-Ясинского при 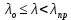 , стержни малой гибкости при , стержни малой гибкости при 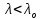 рассчитываются не на устойчивость, а на прочность, так как в данном случае критические напряжения будут равны или немного ниже соответственно пределу текучести рассчитываются не на устойчивость, а на прочность, так как в данном случае критические напряжения будут равны или немного ниже соответственно пределу текучести 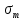 для пластичных материалов (сталь) или пределу прочности для пластичных материалов (сталь) или пределу прочности 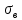 для хрупких материалов (чугун, дерево). для хрупких материалов (чугун, дерево).Таблица 1 Технические характеристики
Расчет на прочность проводится по деформации сжатия: 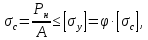 (23) (23)где 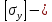 допускаемое напряжение при расчете на устойчивость; допускаемое напряжение при расчете на устойчивость;  коэффициент продольного изгиба; коэффициент продольного изгиба; 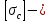 допускаемое напряжение на сжатие. допускаемое напряжение на сжатие.Таблица2 Значения коэффициента продольного изгиба
Математический расчёт. За исходные данные принимаем 11-ый вариант из табл. 3. В расчетах за максимальный вес колонны Q примем рабочую грузоподъемность буровой вышки. Для вышки Н-22: Q= 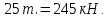 Сила трения при подъеме труб 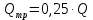 =0,25∙245=61,25 кН. =0,25∙245=61,25 кН. Принимаем среднюю механическую скорость подъема труб V= 1м/c. Тогда время установившегося подъема труб 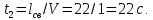 Ускорение движения колонны 𝑎 =V/( 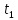 + +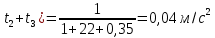 . .Динамические нагрузки 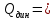 𝑎∙ 𝑎∙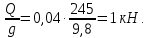 Нагрузка на крюк 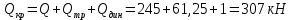 В буровых установках для глубин бурения 1250 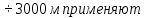 талевые системы с числом шкивов 2 талевые системы с числом шкивов 2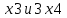 . Примем для нашего случая число шкивов 3х4, где кратность системы равна i=3∙2=6. Усилия в ветвях каната отличаются незначительно, поэтому приравниваем их, то есть . Примем для нашего случая число шкивов 3х4, где кратность системы равна i=3∙2=6. Усилия в ветвях каната отличаются незначительно, поэтому приравниваем их, то есть 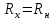 . По эмпирической формуле вес талевой системы . По эмпирической формуле вес талевой системы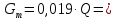 0,019∙245=4,67кН 0,019∙245=4,67кНУсилия в канатах 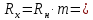 307∙0,177=54,3кН, 307∙0,177=54,3кН,где 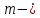 коэффициент, зависящий от оснастки, для системы коэффициент, зависящий от оснастки, для системы 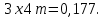 Общая нагрузка на кронблоке 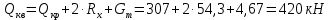 Составляющие силы, действующие в узлах верхнего основания (рис.2). 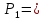 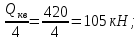 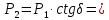 105∙ 105∙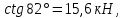 где 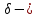 угол наклона оси ноги к горизонту ( угол наклона оси ноги к горизонту (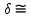 80 80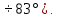 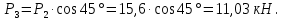 В нижней части ноги вышки 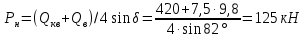 Критическая сила 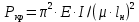 , ,где 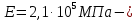 модуль упругости для стали;l=4,5 м - длина ноги в нижней секции; модуль упругости для стали;l=4,5 м - длина ноги в нижней секции;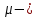 козффициент. Принимаем козффициент. Принимаем 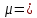 0,8;I – момент инерции сечения ноги вычисляем по формуле 0,8;I – момент инерции сечения ноги вычисляем по формуле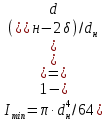 = 3,14∙ 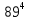 /64∙{1 /64∙{1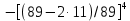 }=1348124 }=1348124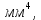 где δ = 11 – толщина стенки ноги вышки. 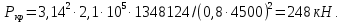 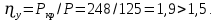 Условие неравенства выполнено. Но формула Эйлера применима лишь при условии 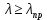 . .Гибкость стержня 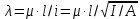 =0,8∙4500/ =0,8∙4500/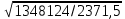 =108,5, =108,5,где i – главный центральный радиус инерции сечения стойки; А – площадь сечения стойки A = π∙( 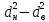 )/4=3,14∙( )/4=3,14∙(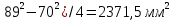 . .𝜆= 108,5 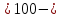 для стальных стержней. для стальных стержней.Предельная гибкость материала стержня 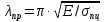 , ,где 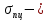 напряжение пропорциональности материала ноги. напряжение пропорциональности материала ноги.Принимаем материал ноги – сталь30, тогда из таблицы 1 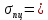 250МПа 250МПа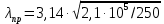 =91 =91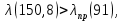 следовательно, Формула Эйлера применима. следовательно, Формула Эйлера применима.Вывод: в ходе проделанной работы мы рассчитали нагрузки на вышку башенного типа, а также сделали проверочный расчет на устойчивость ноги в нижней ее части, используя формулу Эйлера, применимость которой проверена. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||