Отчет по лабораторной работе1 по дисциплине Физика конденсированного состояния
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра МНЭ отчет по лабораторной работе№1 по дисциплине «Физика конденсированного состояния» «Исследование зонной структуры кристаллов»
Санкт-Петербург 2019 ОБРАБОТКА РЕЗУЛЬТАТОВ Расчет энергетического спектра электрона в 3 нижних зонах одномерного кристалла в рамках моделей почти свободных и сильно связанных электронов. а) Модель слабой связи (слабосвязанных электронов): 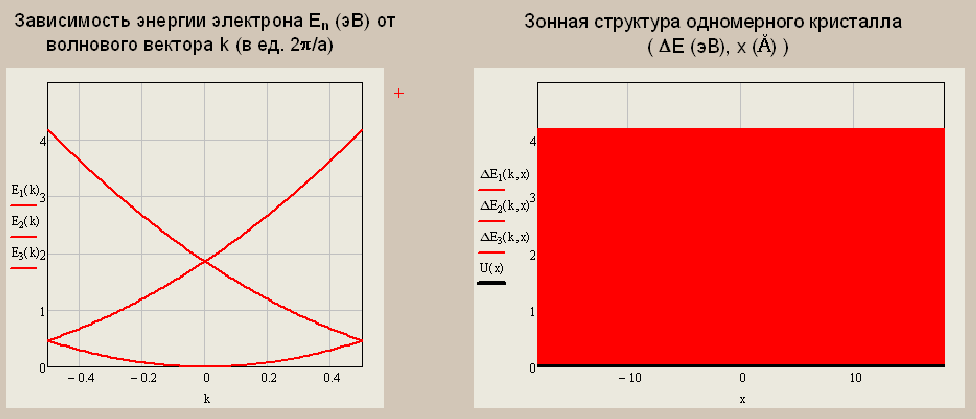 Рисунок1 — Зависимость энергии электрона En от волнового вектора k при U0 = 0и d = 4Å и зонная структура кристалла 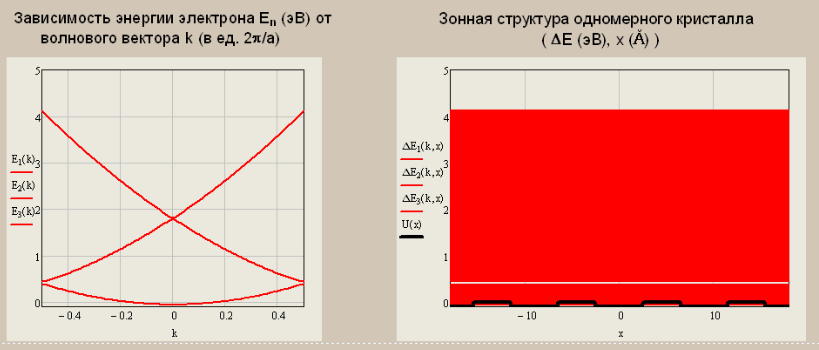 Рисунок 2 —Зависимость энергии электрона En от волнового вектора k при U0 = 0,1эВи d = 4Å и зонная структура кристалла 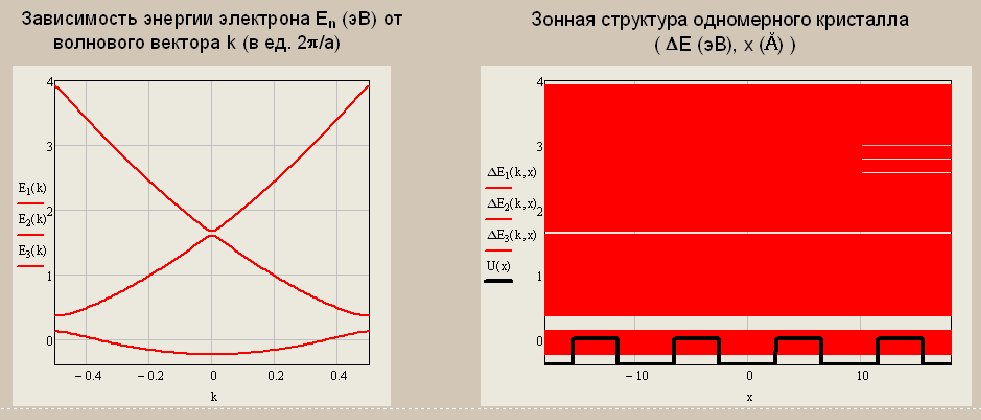 Рисунок 3 — Зависимость энергии электрона En от волнового вектора k при U0 = 0,4эВи d = 4Å и зонная структура кристалла 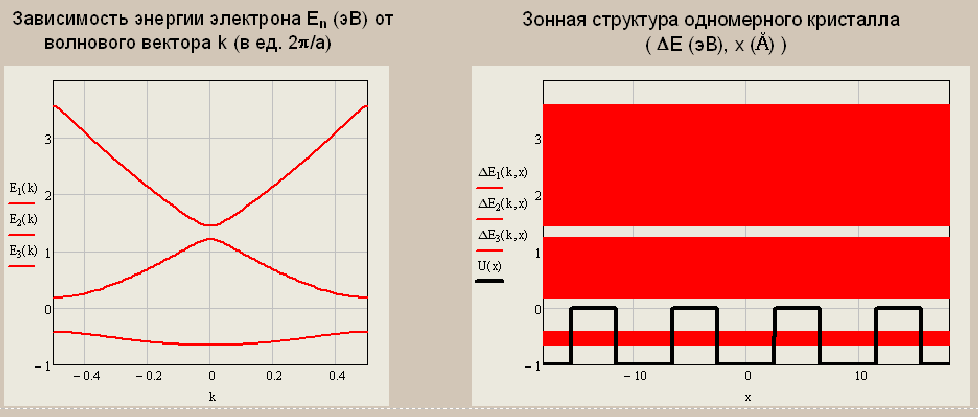 Рисунок 4 — Зависимость энергии электрона En от волнового вектора k при U0 = 1эВ и d = 4Å и зонная структура кристалла 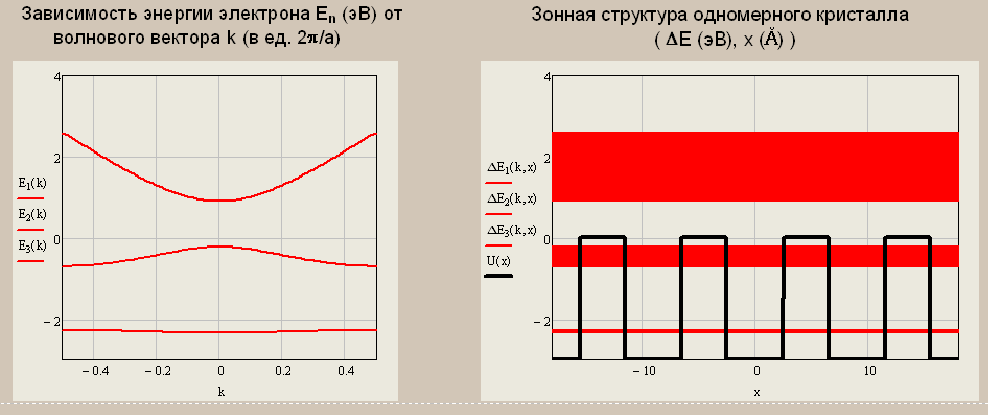 Рисунок 5 — Зависимость энергии электрона En от волнового вектора k при U0 = 3эВ и d = 4Å и зонная структура кристалла 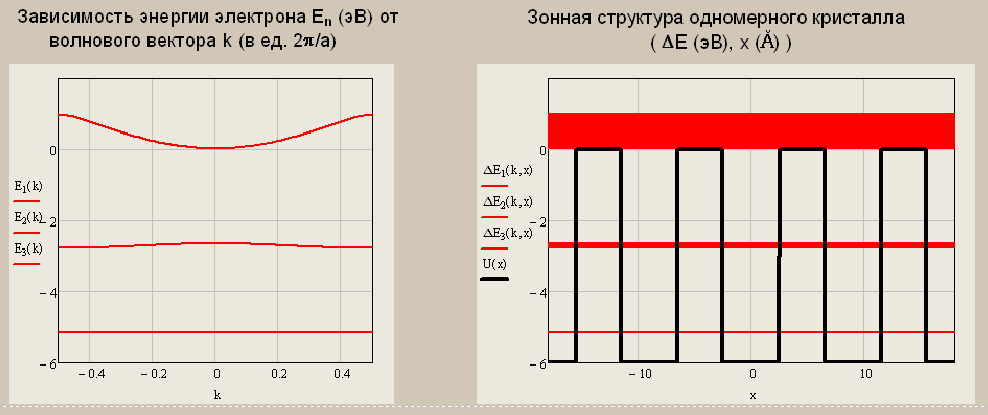 Рисунок 6 — Зависимость энергии электрона En от волнового вектора k при U0 = 6 эВ и d = 4 Å и зонная структура кристалла 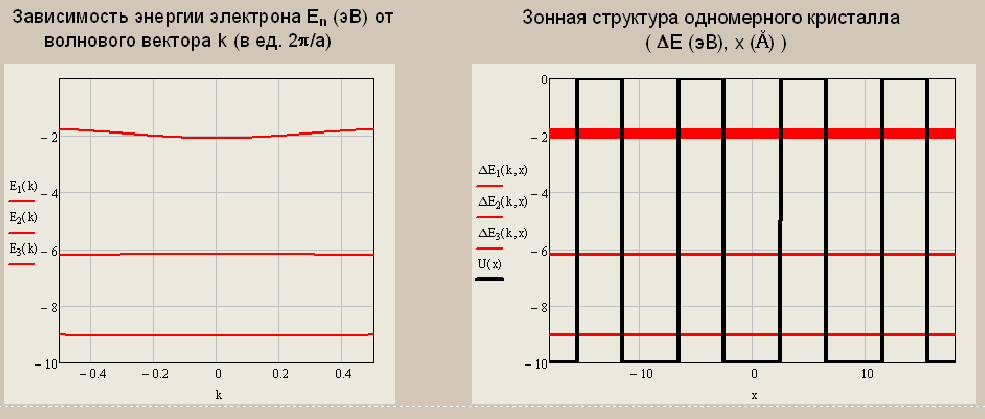 Рисунок 7 — Зависимость энергии электрона En от волнового вектора k при U0 = 10 эВ и d = 4 Å и зонная структура кристалла б) Модель сильной связи (сильносвязанных электронов): 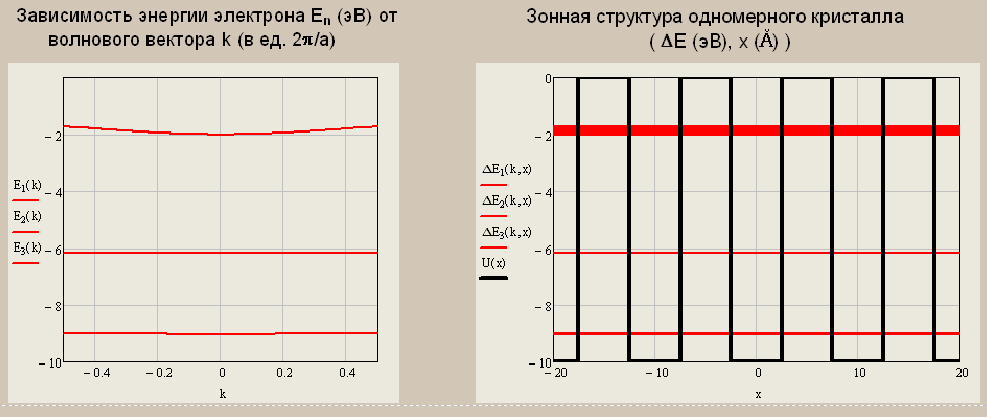 Рисунок 8 — Зависимость энергии электрона En от волнового вектора k при U0 = 10 эВ и d = 5 Å и зонная структура кристалла 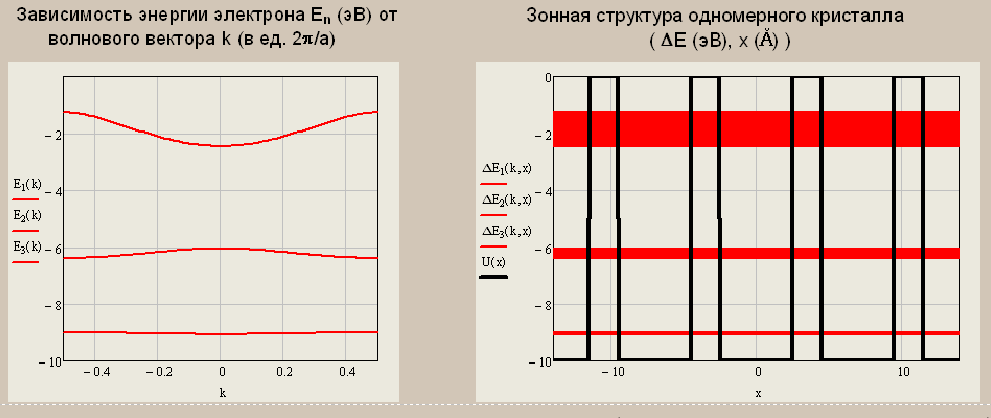 Рисунок 9 — Зависимость энергии электрона En от волнового вектора k при U0 = 10 эВи d = 2 Å и зонная структура кристалла 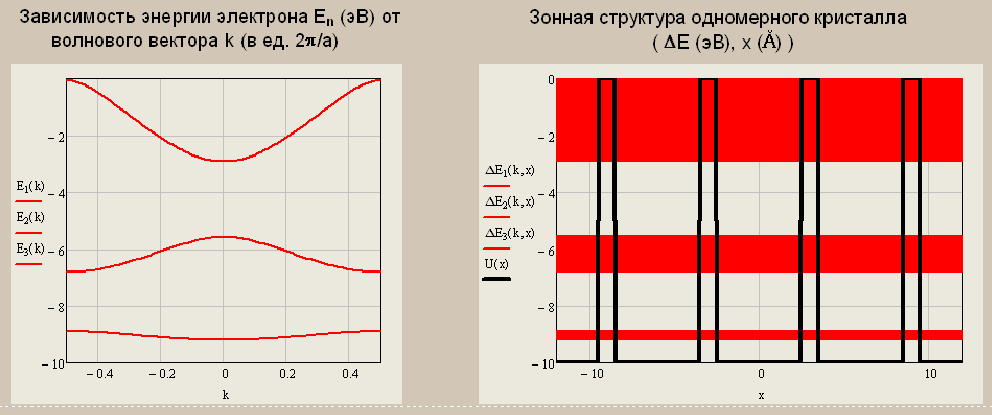 Рисунок 10 — Зависимость энергии электрона En от волнового вектора k при U0 = 10 эВи d = 1 Å и зонная структура кристалла 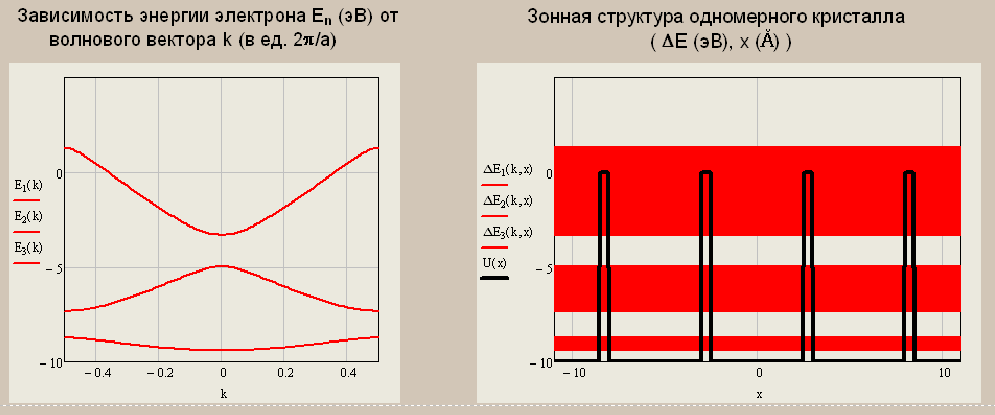 Рисунок 11 — Зависимость энергии электрона En от волнового вектора k при U0 = 10 эВи d = 0,5 Å и зонная структура кристалла 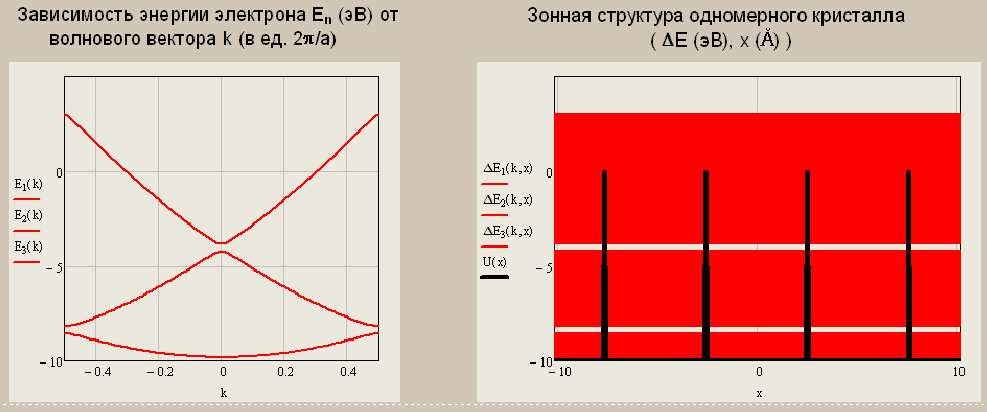 Рисунок 12 — Зависимость энергии электрона En от волнового вектора k при U0 = 10 эВи d = 0,1 Å и зонная структура кристалла 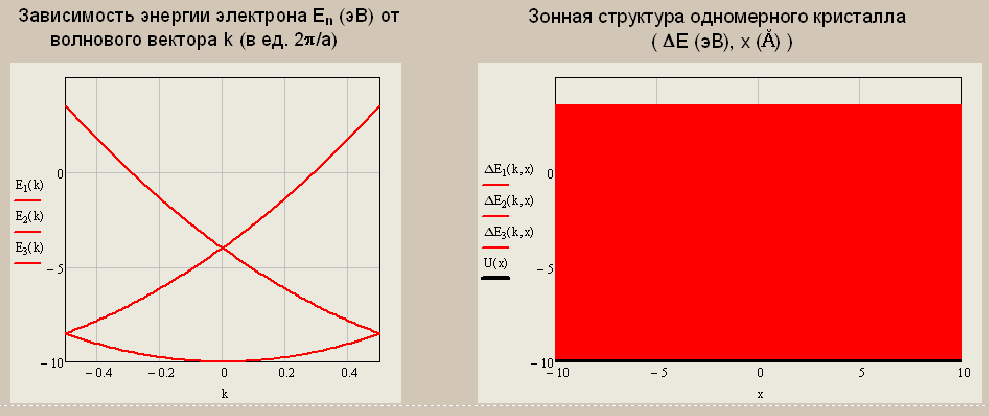 Рисунок 13 — Зависимость энергии электрона En от волнового вектора k при U0 = 10 эВи d = 0 Å и зонная структура кристалла Вывод к первому пункту: приближение слабой связи предполагает, что на электроны действует лишь слабое поле периодического потенциала кристаллической решетки, то есть учитывается лишь периодичность решетки. И электрон в кристалле можно рассматривать как свободный. Также при увеличении периодического потенциала ( речь идет об увеличении потенциальной энергии, создаваемой ионными остовами решетки) появляется и увеличивается ширина запрещенной зоны. Это модель хорошо подходит для описания зонной структуры полупроводников. Важно заметить что в данной модели образуются большие разрешенные зоны и малые запрещенные зоны. Приближение сильно связи учитывает потенциальное поле от каждого атома решетки. Видно что при относительно большой ширине барьера мы имеем большие запрещенные зоны и малые разрешенные. По мере уменьшения d увеличивается разрешенная зона. Также видно, что по мере приближения электрона к атому частица (электрон) попадает в потенциальную яму. И при нулевой ширине барьера d получаем структуру без запрещенной зоны ( получаем вырождение электронных уровней) Такая модель, как правило, применима для описания спектров молекулярных кристаллов, окислов. Расчет волновых функций электрона в 3-х нижних зонах при k = 0, U0 = 5 В. 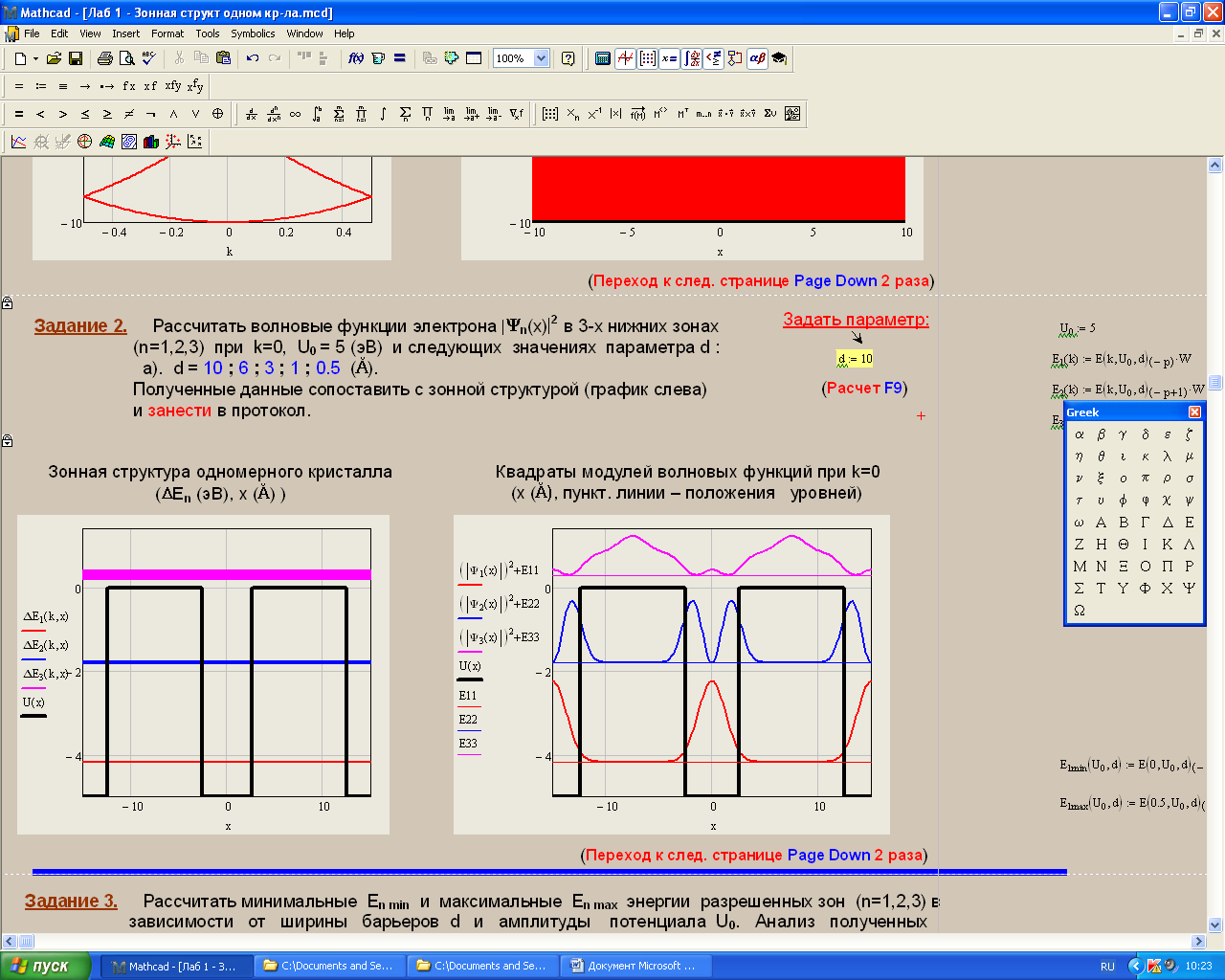  Рисунок 14 — Зонная структура кристалла и квадрат волновых функций электрона(ΔEn (эВ),x (Ă)) при n = 1,2,3 при k = 0, U0 = 5 эВ, d = 10Ă 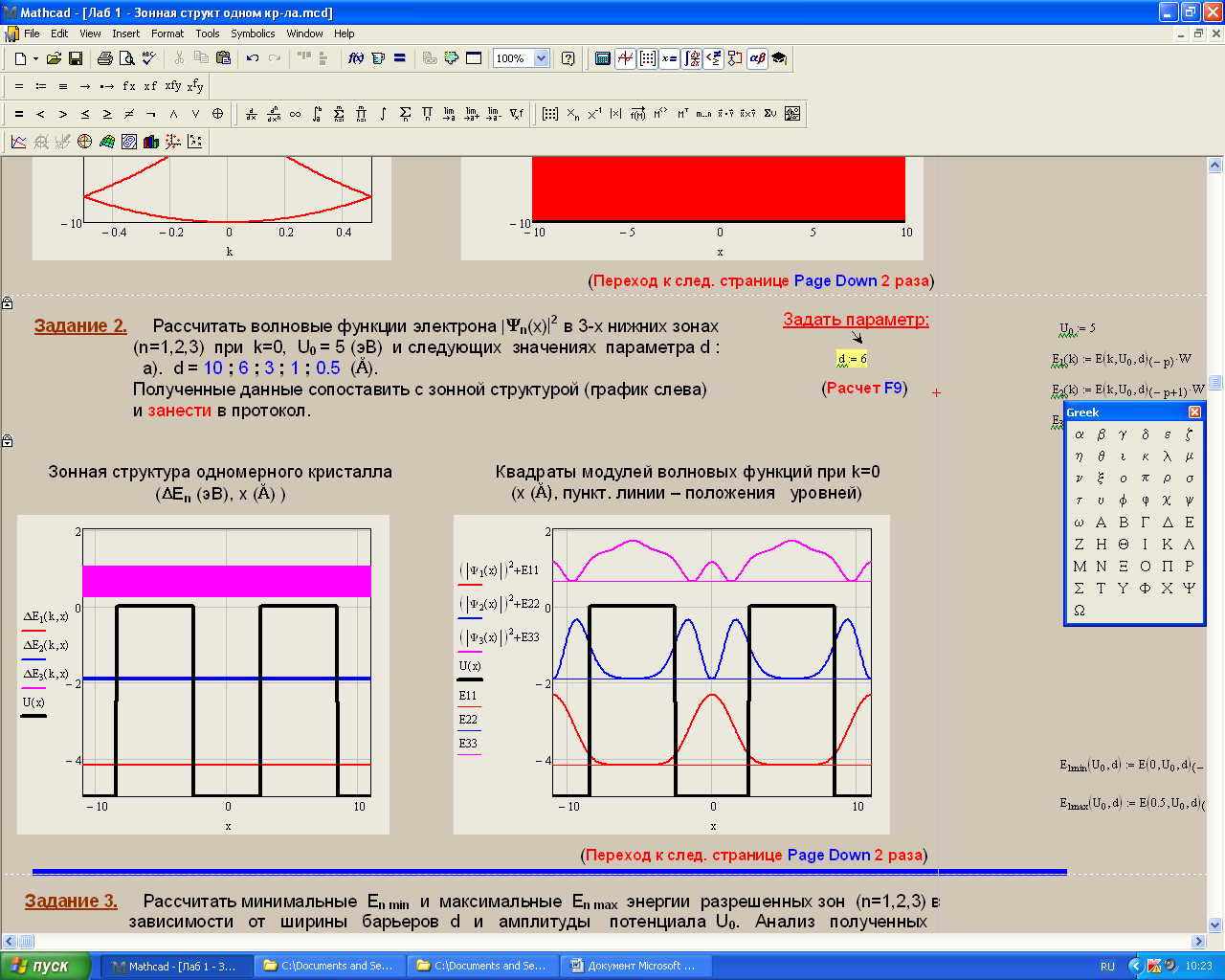  Рисунок 15 — Зонная структура кристалла и квадрат волновых функций электрона(ΔEn (эВ),x (Ă)) при n = 1,2,3 при k = 0, U0 = 5 эВ, d = 6Ă 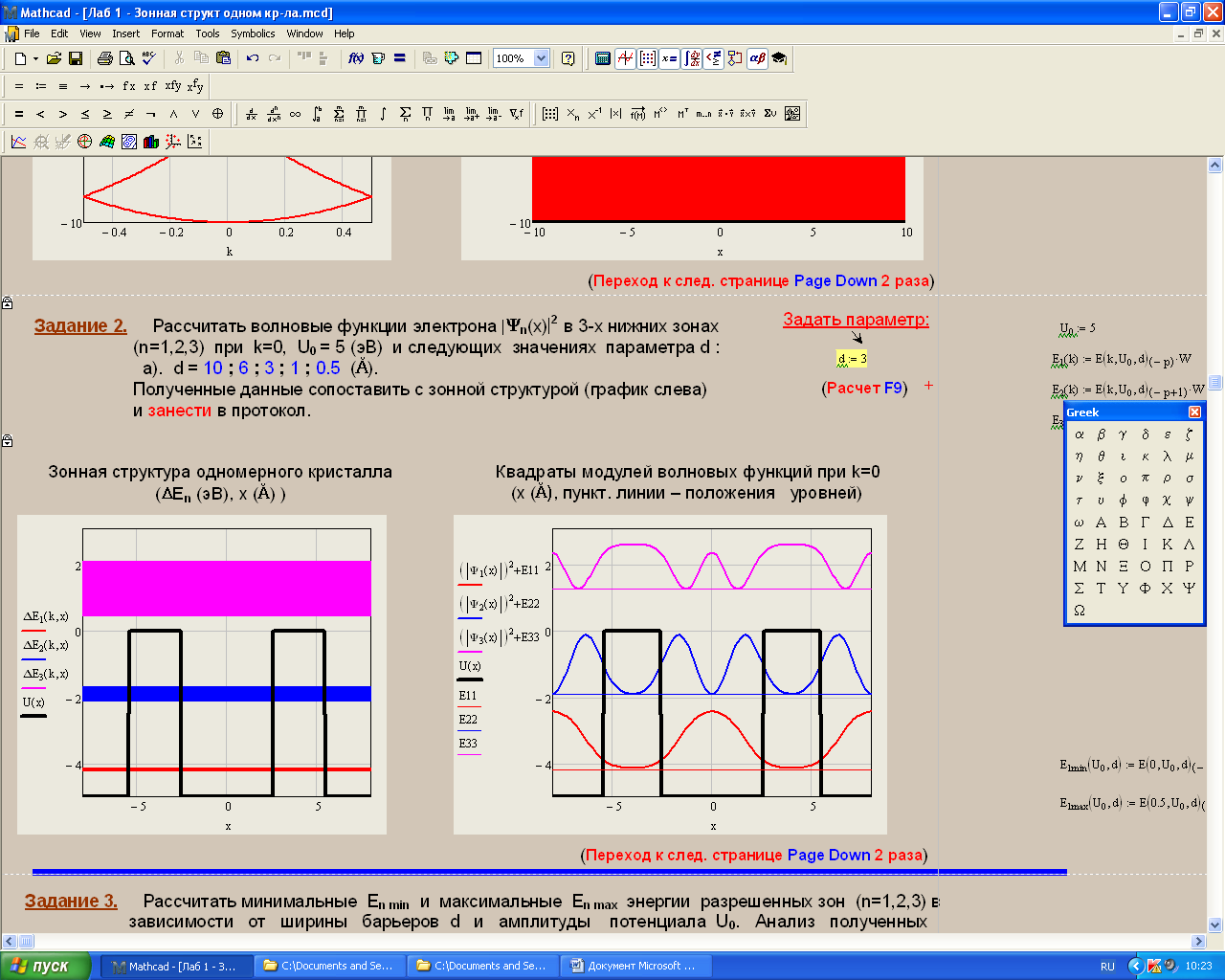  Рисунок 16 — Зонная структура кристалла и квадрат волновых функций электрона(ΔEn (эВ),x (Ă)) при n = 1,2,3 при k = 0, U0 = 5 эВ, d = 3Ă 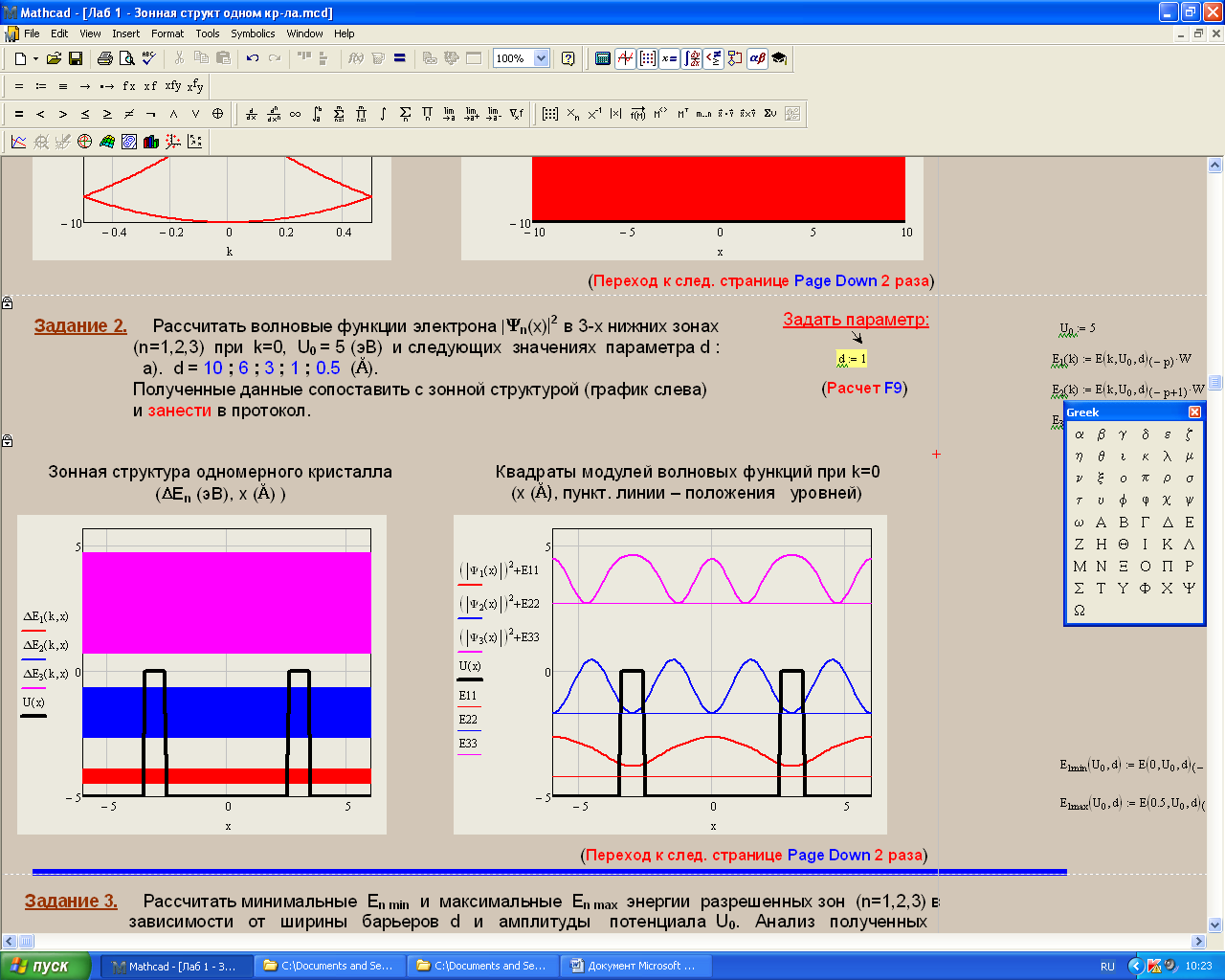  Рисунок 17 — Зонная структура кристалла и квадрат волновых функций электрона(ΔEn (эВ),x (Ă)) при n = 1,2,3 при k = 0, U0 = 5 эВ, d = 1Ă 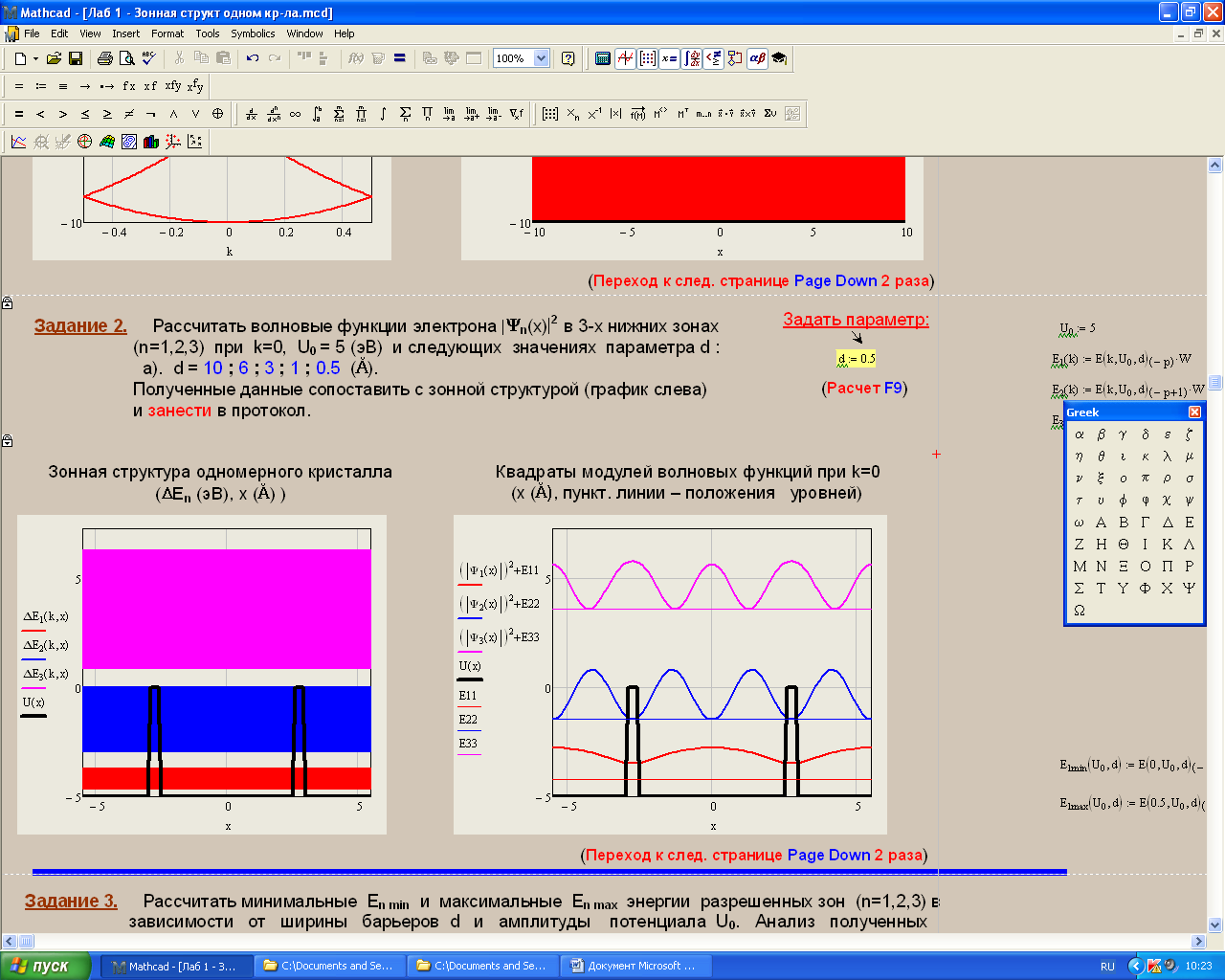  Рисунок 18 — Зонная структура кристалла и квадрат волновых функций электрона(ΔEn (эВ),x (Ă)) при n = 1,2,3 при k = 0, U0 = 5 эВ, d = 0.5Ă Вывод ко 2 пункту: для волновых функций, соответствующих 1 и 2 энергетическим зонам (n=1, 2) квадрат волновой функции минимален в местах, где максимален потенциал решетки, т.е. между узлами решетки. При уменьшении d ( ширины барьера) увеличиваются разрешенные зоны. Квадрат модуля волновых функций, соответствующих n=2,3 стремится к гармоническим функциям ( синус, косинус), а при n=1 плотность вероятности стремится к постоянному значению. То есть при уменьшении d увеличивается вероятность обнаружить частицу в потенциальной яме. Расчет зависимости минимальных и максимальных энергий разрешенных зон при n = 1, 2, 3 в зависимости от ширины барьеров и амплитуды потенциала U0 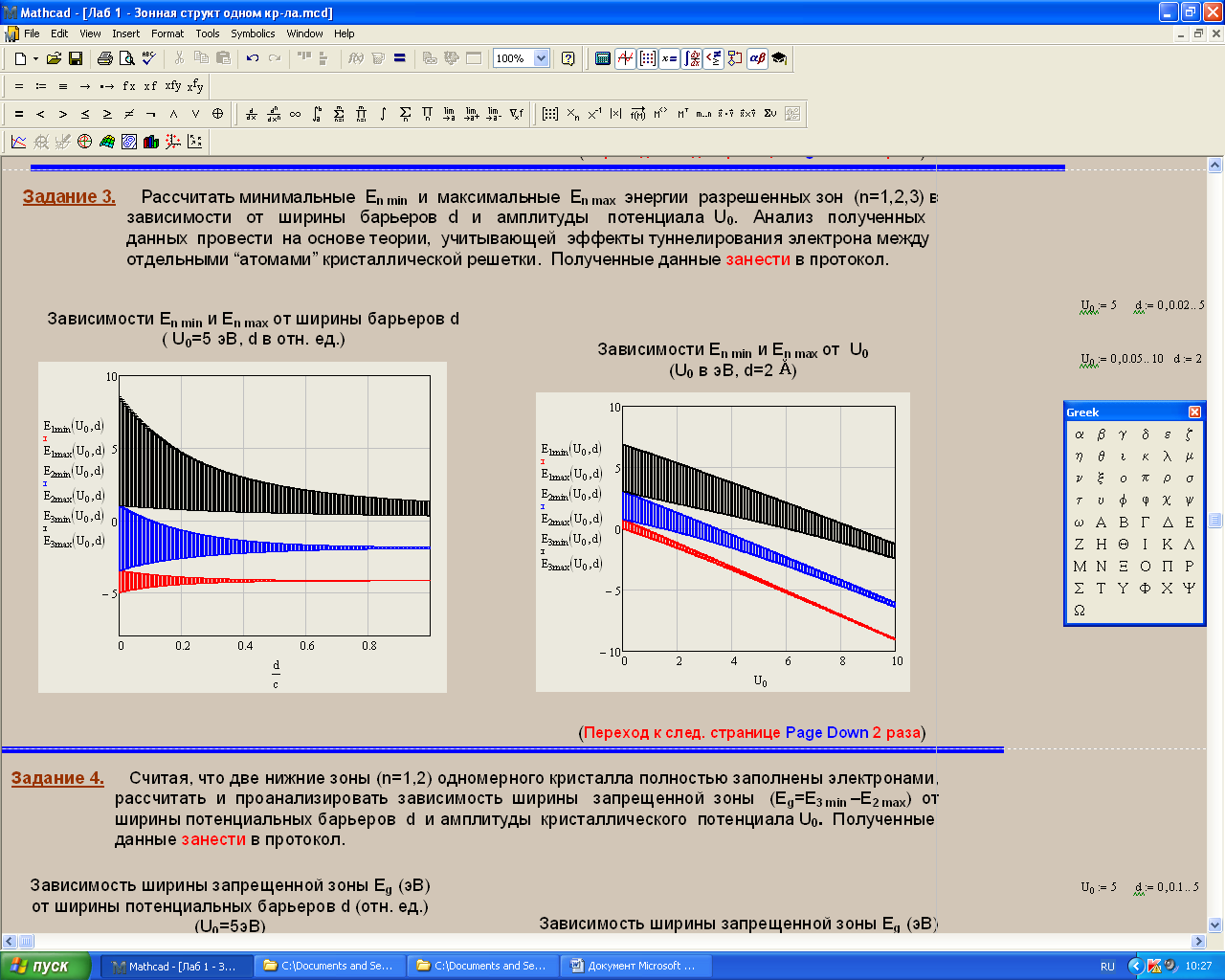 Рисунок 19 — Зависимость Enmin и Enmax(эВ) от d/c (отн. ед.) при n = 1,2,3 при U0 = 5В  Рисунок 20 — Зависимость Enmin и Enmax(эВ) от U0 (эВ) при n = 1,2,3 при d = 2Ă Вывод к третьему пункту: Из рис. 19 видно, что при увеличении ширины потенциального барьера ( при уменьшении ширины потенциальной ямы) сужаются разрешенные зоны. Что полностью совпадает с результатами пункта 1 для модели сильной связи. Из рис. 20: при увеличении амплитуды потенциала U0 сужаются разрешенные зоны. И это совпадает с результатами пункта 1 для модели слабой связи. Расчет зависимости ширины запрещенной зоны (Eg = E3min-E2max) от ширины потенциальных барьеров d и амплитуды потенциала U0, считая, что зоны n=1, 2 полностью заполнены электронами. 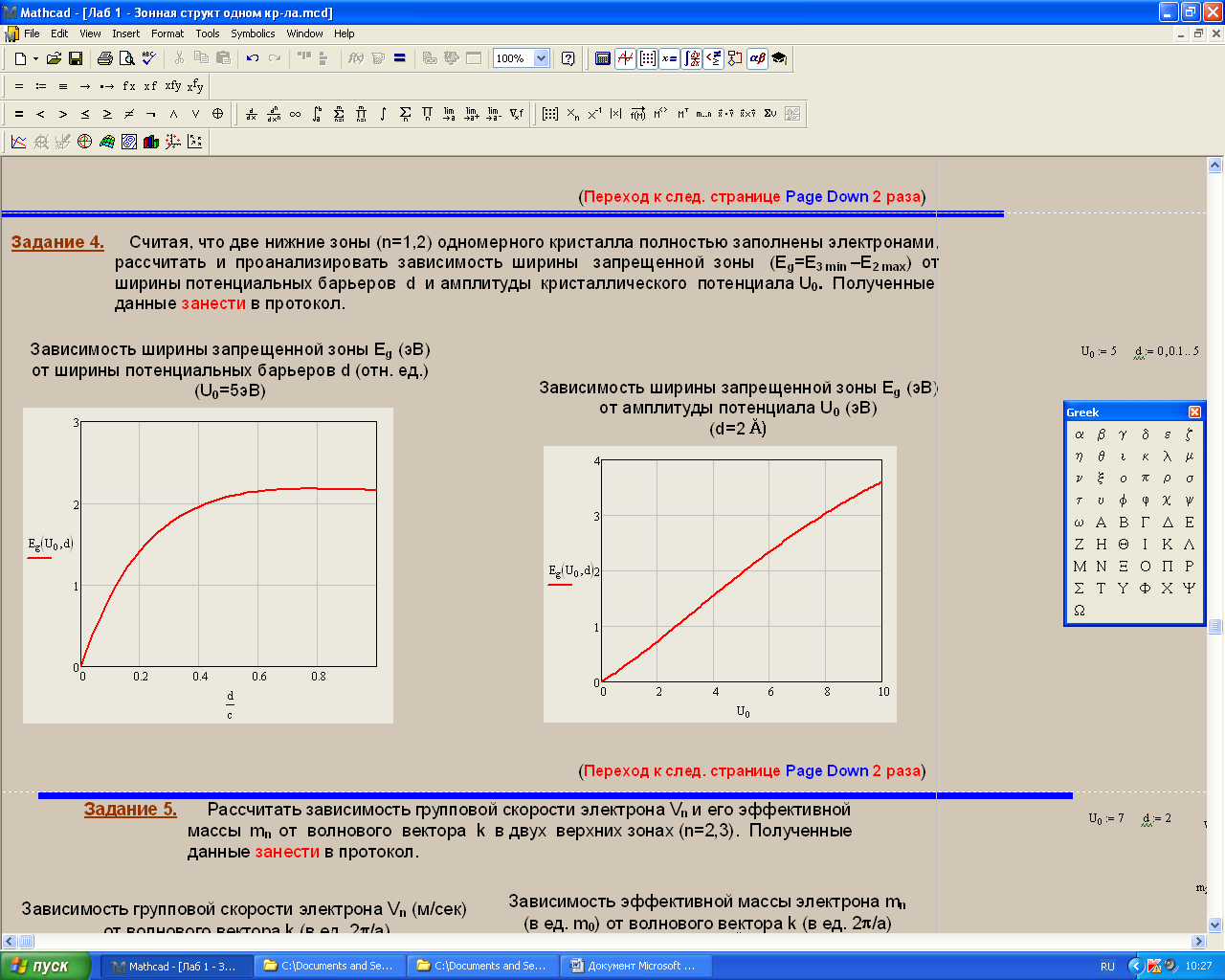 Рисунок 21 —Зависимость Eg = E3min - E2max (эВ) от d (отн. ед.) при U0 = 5 эВ  Рисунок 22 — Зависимость Eg = E3min-E2max (эВ) от U0 (эВ) при d = 2 Ă Вывод к четвертому пункту: Из рисунка 21 видно, что при увеличении d (уменьшении с) увеличивается ширина запрещенной зоны. Эти результаты совпадают с результатами в 1 и 3 пунктах. Из рисунка 22 также наблюдается увеличение ширины запрещенной зоны при увеличении U0. Нет никаких противоречий с 1 и 3 пунктом лабораторной работы. Расчет зависимости групповой скорости электрона vгр и его эффективной массы m* от волнового вектора электрона k в двух верхних зонах 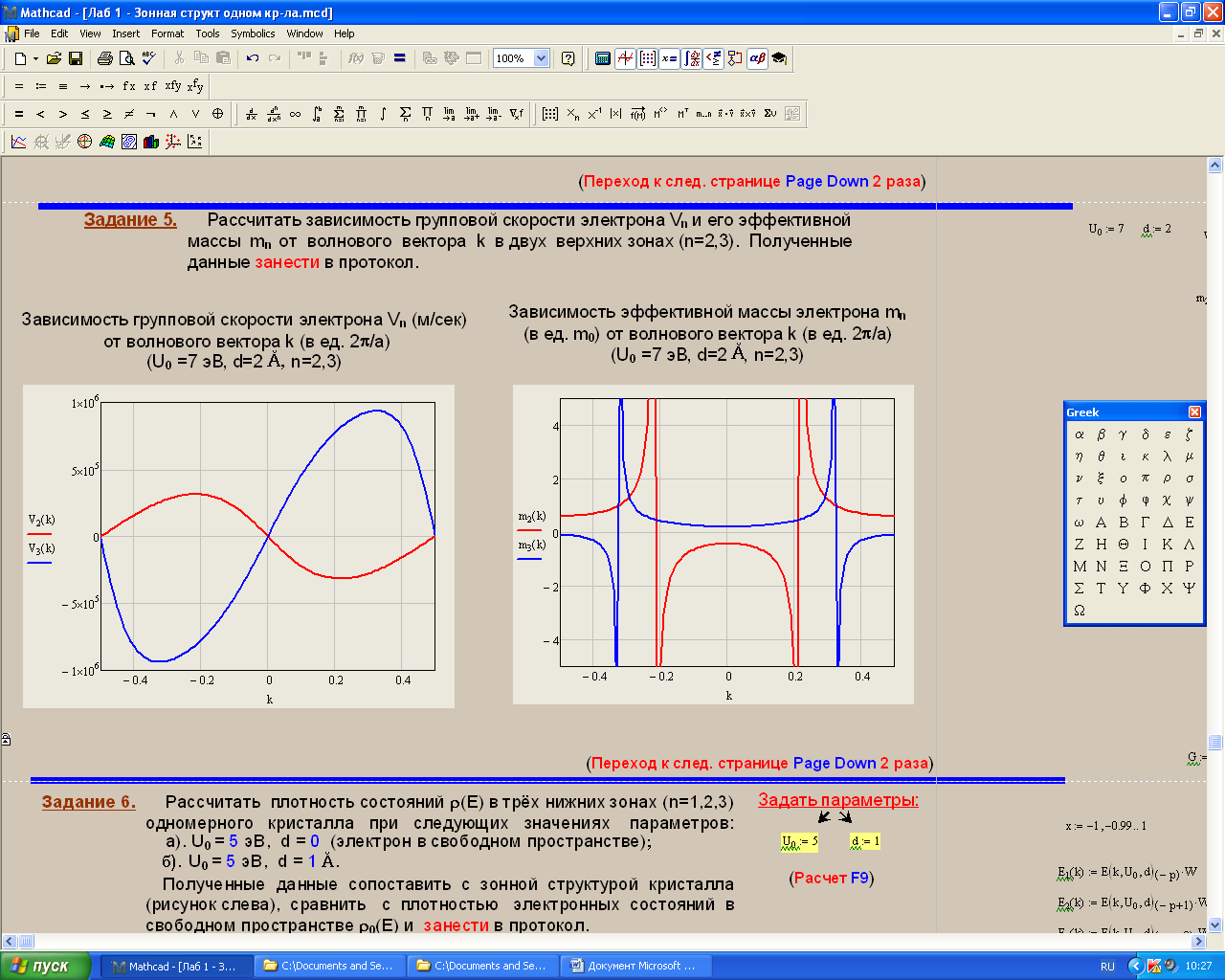 Рисунок 23 — Зависимость vгр(м/сек) от k (в ед. 2π/a) при U0 = 7 эВ, d = 2Ă, n = 2, 3  Рисунок 24 — Зависимость m*(в ед. m0) от k (в ед. 2π/a) при U0 = 7 В, d = 2 Ă, n = 2, 3 Вывод к пятому пункту: видно что для второй, что для первой зоны выполняется теорема о скорости. Из рисунка 23 следует, что при к = 0 мы имеем нулевую скорость. К примеру из рис 3- 5 мы видим экстремум у графика функции Е(к) , следовательно 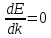 , тогда и V=0 при к=0. Из рисунка 24 видно, что при к →0 (в окрестности 0) имеем постоянную эффективную массу. , тогда и V=0 при к=0. Из рисунка 24 видно, что при к →0 (в окрестности 0) имеем постоянную эффективную массу. Расчет плотности состояний ρ(E) при n = 1, 2, 3 при двух разных случаях а) U0 = 5эВ, d = 0 (электрон в свободном пространстве) 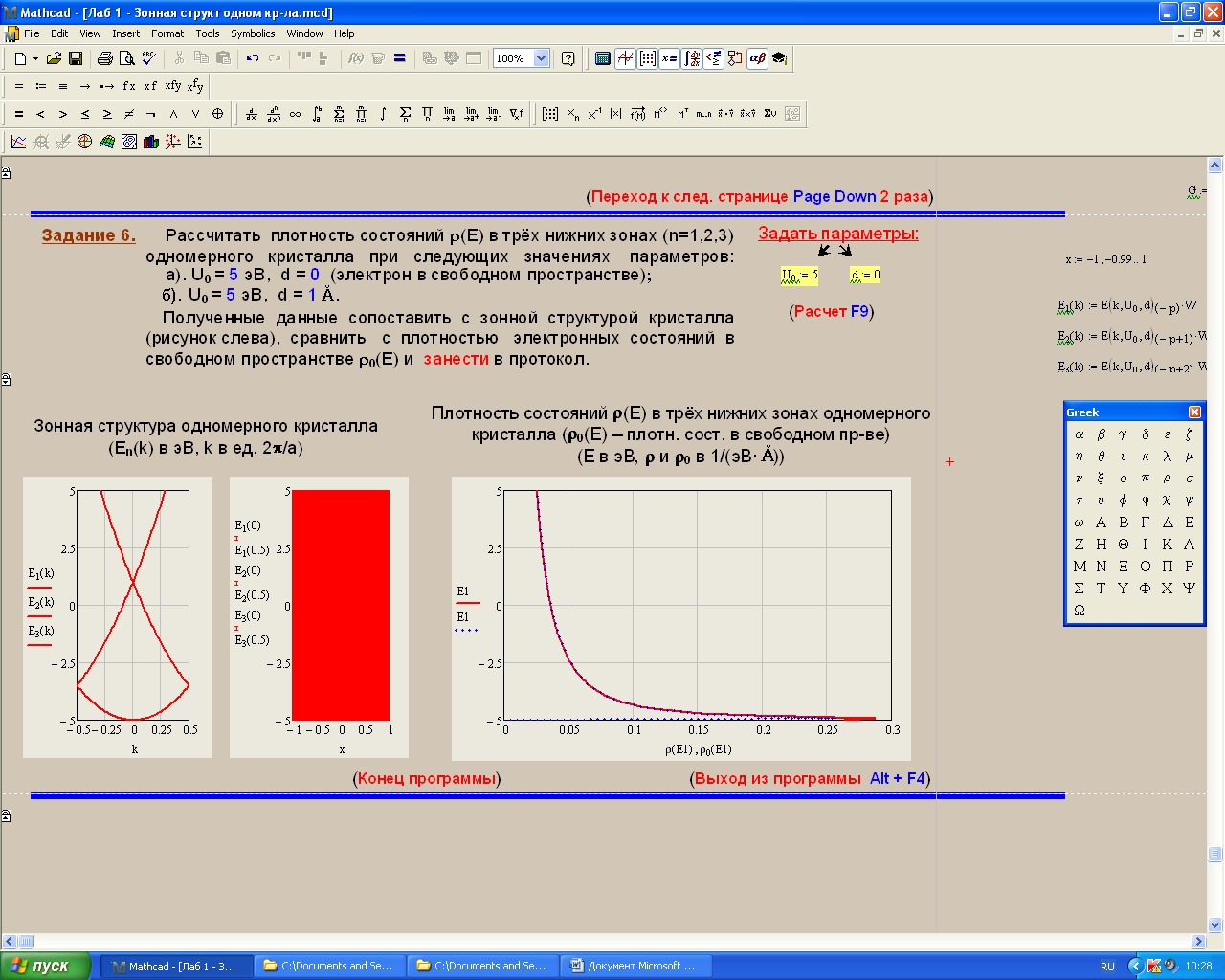 Рисунок 25 —Зонная структура одномерного кристалла (En(k) в эВ, k в ед. 2π/a)  Рисунок 26 —Плотность состояний ρ(E) в трех нижних зонах (ρ0(E) – плотность состояний в свободном пространстве), (E в эВ, ρ и ρ0 в 1/(эВ*Ă)) б) U0 = 5В, d = 1Ă 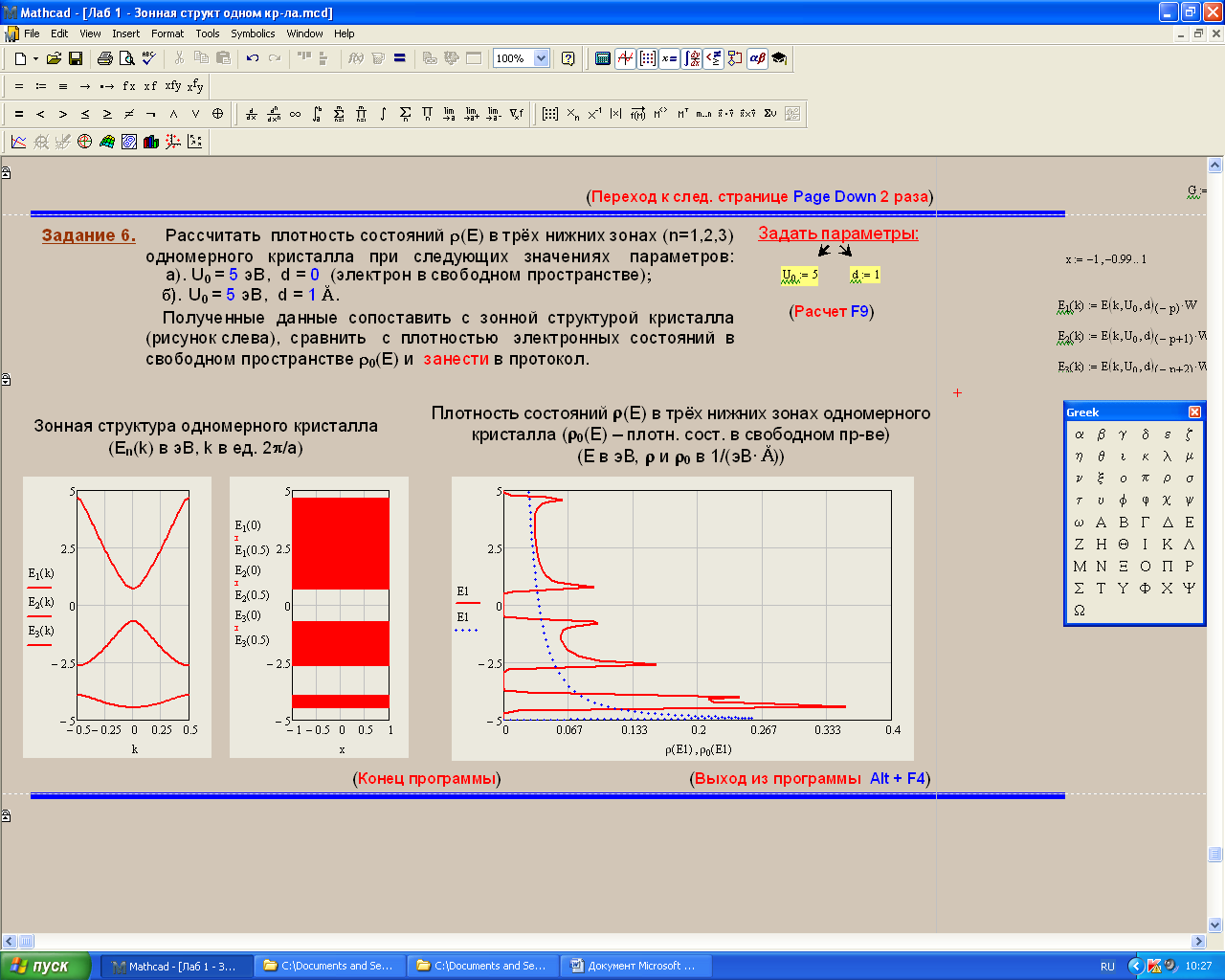 Рисунок 27 — Зонная структура одномерного кристалла (En(k) в эВ, k в ед. 2π/a)  Рисунок 28 — Плотность состояний ρ(E) в трех нижних зонах (ρ0(E) – плотность состояний в свободном пространстве), (E в эВ, ρ и ρ0 в 1/(эВ*Ă)) Вывод к шестому пункту: Когда электрон находится в свободном пространстве мы получаем квазинепрерывную энергетическую зону и элетктрон может находиться в любом энергетическом состоянии и рисунок 26 отражает вероятность обнаружить электрон с энергией Е. Исходя из рисунков 28 и 27 при d = 1Ă видно, что появляются запрещенные зоны. При этом распределение запрещенных зон на рисунке 27 совпадает с зависимостью на рисунке 28. К примеру: на рисунке 28 на промежутке от -2,5 до 0 эВ (примерно) плотность вероятности ρ(E) ≠ 0, что соответствует разрешенной зоне на рисунке 27. И на промежутке (рис 28) от -3 до -2,5 (примерно) ρ(E) = 0, что соответствует запрещенной зоне на рисунке 27. |
