Надежность подвижного состава. Отчет по практическим работам 1, 2, 3 по дисциплине "Надежность электроподвижного состава"
 Скачать 180.52 Kb. Скачать 180.52 Kb.
|
|
Расчетное значение критерия Пирсона χ2расч= 6,515 Критическое значение критерия Пирсона χ²крит = 7,78. Так какχ²расч < χ²крит, то случайная величина принадлежит закону нормального распределения. ЗАДАНИЕ на практические работы № 1, 2 и 3 по дисциплине «Надежность подвижного состава» (1 часть 1 работы) Студент Гриценко Павел Александрович Форма обучения очная Группа ПСт-426 Исходные данные: Значения наработки устройства до отказаи заданное значение L и L0
Задание Выдано: «4» сентября 2019 г. ПЛАН-ГРАФИК выполнения практических работ по дисциплине «Надежность подвижного состава» Студент Гриценко Павел Александрович Форма обучения очная Группа ПСт-426 Номер варианта 86 Тема практических работ Надежность подвижного состава
Дата 4.09.2019 г. Подпись студента Дата 4.09.2019 г. Подпись руководителя 1 Расчет числовых характеристик закона распределения контролируемого параметра Случайная величина будет полностью описана с вероятностной точки зрения, если определить закон ее распределения, под которым понимается определенное соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Контролируемые параметр изнашиваемой детали является непрерывной случайной величиной, закон распределения которой моет быть представлен плотностью распределения. Среднее значение контролируемого параметра Y в i-м сечении: 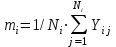 . (1) . (1)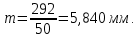 Среднеквадратическое отклонение контролируемого параметра: 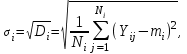 (2) (2)где Ni – число значений контролируемого параметра на замер с данным номером i (в i-ом сечении). 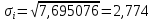 мм. мм.Для построения плотности распределения контролируемого параметра область его определения делится на K интервалов и подсчитываются величины nj – число значений контролируемого параметра, попавших в j-ый интервал, где j = 1, 2,..., K. Число интервалов разбиения определим используя правило Страджесса: K = 1 + 3,3 lg n, (3) где n – объем выборки статистической совокупности (для j-го сечения). K = 1 + 3,3 lg 50 = 7. Частота попаданий контролируемого параметра в j-й интервал определяем по формуле: 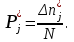 (4) (4)Высота прямоугольника определяется как: 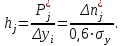 (5) (5)Длина частичного разряда определяется из формулы: 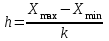 , (6) , (6)где Хmax– максимальное значение из исходных данных; Хmin– минимальное значение из исходных данных; K–число интервалов разбиения. 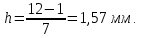 . Таблица 1 – Расчетные значения
Контролируемые параметры изнашиваемых деталей ЭПС хорошо описываются нормальным законом, плотность распределения которого 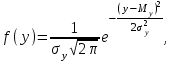 (7) (7)где Mx – математическое ожидание контролируемого параметра; σ – среднеквадратическое отклонение контролируемого параметра; X– текущее значение контролируемого параметра. Расчетное значение критерия Пирсона определяется как: 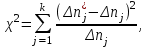 (8) (8)где nj – теоретическое число значений случайной величины в j-м интервале. 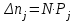 , (9) , (9)где Pj – теоретическая вероятность попадания случайной величины в j-ый интервал. Теоретическая вероятность попадания случайной величины в j-ый интервал определяется зависимостью: 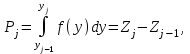 (10) (10)где yj–1– левая граница j-го интервала; yj– правая граница j-го интервала; Zj– значение функции распределения в точке yj; Zj–1– то же в точке yj–1.  f(y),1/мм     Y, мм 0,14 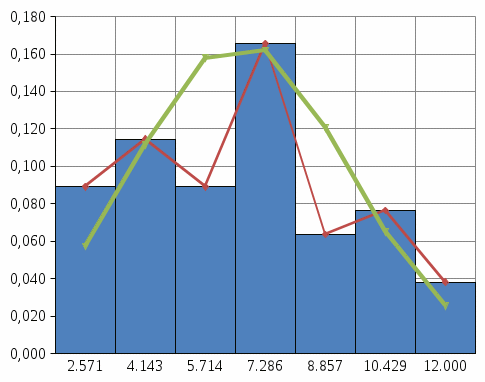 Рисунок 1– Постоянное распределение величины проката бандажа колесных пар электровозов Таблица 2 – Полученные значения по графику распределения
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
