Надежность подвижного состава. Отчет по практическим работам 1, 2, 3 по дисциплине "Надежность электроподвижного состава"
 Скачать 180.52 Kb. Скачать 180.52 Kb.
|
|
3 Определение ресурса изнашиваемых деталей На основании полученных зависимостейmy(L) и y(L)можно прогнозировать процесс изнашивания и определить ресурс деталей ЭПС. Для этого зависимости my(L) и y(L)экстраполируются в область больших значений пробега в предположении, что характер этих зависимостей не изменится, т.е. изнашивание детали останется в пределах нормальной эксплуатации (участок 2, рисунок 2), что обеспечивается надлежащим выбором допуска на износ рассматриваемой детали. Подставив значение пробега L в выражения my(L) и y(L),рассчитаем числовые характеристики распределения контролируемого параметра в области экстраполяции и построим кривые плотности распределения. Начальный пробег LН, для увеличивающегося контролируемого параметра, при котором будет вычислено первое значение вероятности отказа, близкое к нулю, определим по формуле: 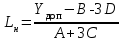 ; (12) ; (12)где Yдоп – допустимое значение параметра; A,B,C,D – коэффициенты зависимостейmy(L) и y(L) 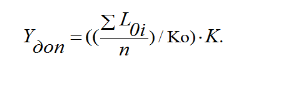 (13) (13)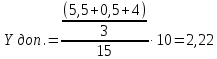 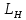 = = 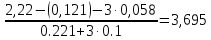 тыс.км. тыс.км.Пробег, соответствующий вероятности отказа P = 0,5, определяется соотношением 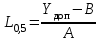 ; (14) ; (14)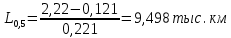 Шаг изменения пробега ∆L при расчете возможных значений зависимости P(L)определим исходя из формулы 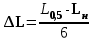 ; (15) ; (15)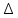 L= L= 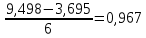 тыс.км. тыс.км.Для увеличивающегося контролируемого параметра вероятность отказа при заданном пробеге определяется зависимостью: 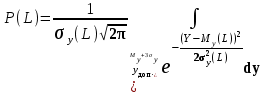 . (23) . (23)Таблица 4 – Полученные значения для построения графика
На основании выполненных расчетов построили зависимость P(L) (рисунок 6). По рисунку 6 определили 90 %-ный ресурс детали, т.е. такой пробег, которому соответствует вероятность безотказной работы или вероятность отказа P = 1 – W=0,1 и получили пробег L=5,629тыс. км.     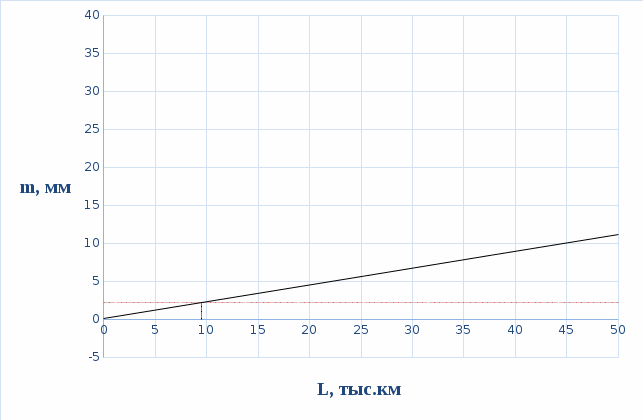     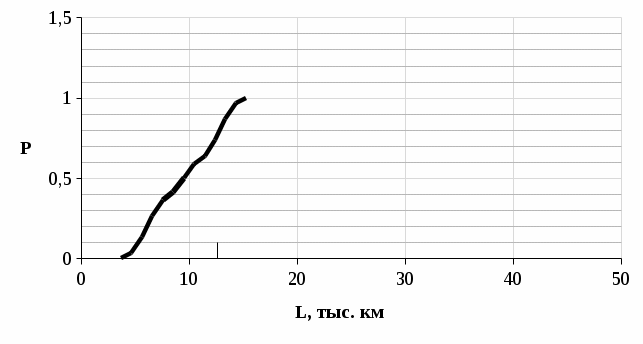     L, тыс.км Рисунок 6 – Прогнозирование процесса изнашивания деталей ЭПС Заключение По результатам расчетов числовых характеристик выполнили аппроксимирование в результате, которого мы получили теоретические зависимости m(L)= y = 1,813x - 5,161 и ϭ(L)= y = 0,115x + 0,765. За тем подставили значения пробега L в выражения m(L) и ϭ(L). Из которых нашли начальный пробег первого отклонения Lн= 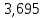 тыс.км., шаг изменения пробега ΔL = тыс.км., шаг изменения пробега ΔL = 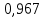 тыс. км, и пробег, соответствующий вероятности отказа при P=0,5 тыс. км, и пробег, соответствующий вероятности отказа при P=0,5 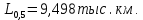 |
