Надежность подвижного состава. Отчет по практическим работам 1, 2, 3 по дисциплине "Надежность электроподвижного состава"
 Скачать 180.52 Kb. Скачать 180.52 Kb.
|
|
Расчетное значение критерия Пирсона χ2расч= 6,515. Критическое значение критерия Пирсона χ²крит = 6,25. Так как χ²расч > χ²крит, то случайная величина не принадлежит закону нормального распределения. ЗАДАНИЕ на практические работы № 1, 2 и 3 по дисциплине «Надежность подвижного состава» (1 часть 1 работы) Студент Аникин Даниил Владимирович Форма обучения очная Группа ПСт-426 Исходные данные: ТаблицаЗначения наработки устройства до отказа и заданное значение L и L0
Задание Выдано: « 04 » сентября 2019 г. ПЛАН-ГРАФИК выполнения практических работ №№ 1, 2 и 3 (часть 1) по дисциплине «Надежность подвижного состава» Студент Аникин Даниил Владимирович Форма обучения очная № зач. кн. 20161488 Группа ПСт-426 Номер варианта 81 Тема работы Надежность подвижного состава
Дата 4.09.2019 г. Подпись студента Дата 4.09.2019 г. Подпись руководителя 1 Расчет числовых характеристик закона распределения контролируемого параметра Случайная величина будет полностью описана с вероятностной точки зрения, если определить закон ее распределения, под которым понимается определенное соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Контролируемые параметр изнашиваемой детали является непрерывной случайной величиной, закон распределения которой моет быть представлен плотностью распределения. Среднее значение контролируемого параметра Y в i-м сечении: 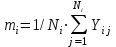 . (1) . (1)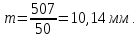 Среднеквадратическое отклонение контролируемого параметра: 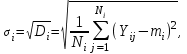 (2) (2)где Ni – число значений контролируемого параметра на замер с данным номером i (в i-ом сечении). 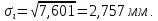 Для построения плотности распределения контролируемого параметра область его определения делится на K интервалов и подсчитываются величины nj – число значений контролируемого параметра, попавших в j-ый интервал, где j = 1, 2,..., K. Число интервалов разбиения определим используя правило Страджесса: K = 1 + 3,3 lgn, (3) где n – объем выборки статистической совокупности (для j-го сечения). K = 1 + 3,3 lg50 = 7. Длина частичного разряда определяется из формулы: 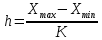 (4) (4)где Хmax – максимальное значение из исходных данных; Хmin– минимальное значение из исходных данных; K–число интервалов разбиения. . 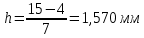 Таблица 1 – Расчетные значения
Контролируемые параметры изнашиваемых деталей ЭПС хорошо описываются нормальным законом, плотность распределения которого 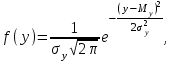 (7) (7)где Mx– математическое ожидание контролируемого параметра; σ –среднеквадратическое отклонение контролируемого параметра; X– текущее значение контролируемого параметра. Расчетное значение критерия Пирсона определяется как: 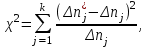 (8) (8)где nj – теоретическое число значений случайной величины в j-м интервале. 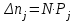 , (9) , (9)где Pj – теоретическая вероятность попадания случайной величины в j-ый интервал. Теоретическая вероятность попадания случайной величины в j-ый интервал определяется зависимостью: 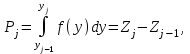 (10) (10)где yj–1– левая граница j-го интервала; yj– правая граница j-го интервала; Zj– значение функции распределения в точке yj; Zj–1– то же в точке yj–1.Р     Y,мм f(y),1/мм 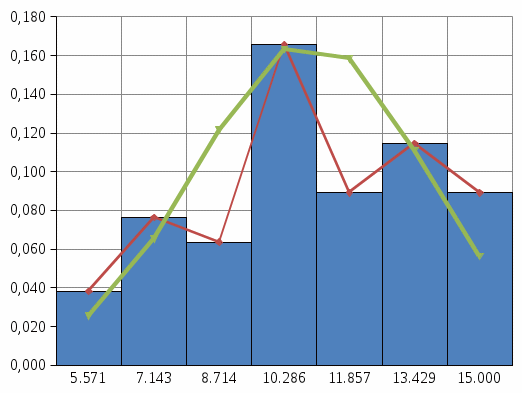 Рисунок 1 - Постоянное распределение величины Таблица 2 – Полученные значения по графику распределения
Расчетное значение критерия Пирсона χ2расч= 6,710 Критическое значение критерия Пирсона χ²крит = 6,250 Так какχ²расч > χ²крит, то случайная величина не принадлежит закону нормального распределения. 2 Определение зависимости числовых характеристик от пробега Согласно представлениям теории изнашивания [6] считается, что кривая износа имеет вид, представленный на рисунке 2. 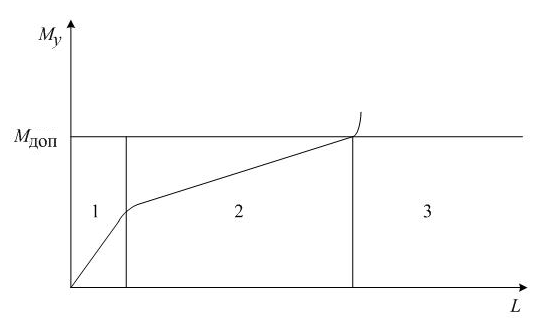 1 – приработочный период; 2 – период нормальной эксплуатации; 3 – период усиленного износа. Рисунок2 – Зависимость величины износа узлов электроподвижного состава от пробега Рассмотрим второй участок функции – период нормальной эксплуатации, где зависимость контролируемых параметров от пробега близка к линейной [3]. Об этом свидетельствует анализ полей корреляции числовых характеристик контролируемых параметров, представленных на рисунках 3 и 4. Таблица 3 – Результаты расчетов числовых характеристик
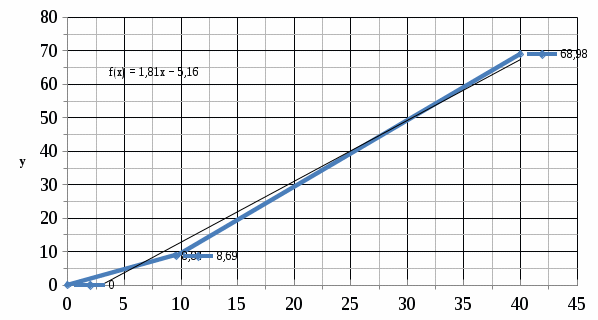 Рисунок 3 – Зависимость среднего значения контролируемого параметра от пробега 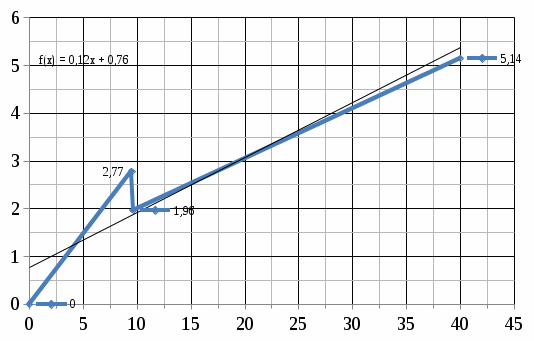 Рисунок 4 – Зависимость среднеквадратического отклонения контролируемого параметра от пробега Выполним аппроксимирование, расчет коэффициентов корреляции при помощи таблиц Excel, зависимости представлены на рисунках. Коэффициент корреляции используется в теории вероятностей для характеристики тесноты связи между случайными величинами Y и L. Rml = 0,998; Rσl = 0,870; Если коэффициент корреляции больше или равен 0,8, то можно заменить практическую зависимость теоретической. Определим величину остаточной дисперсии по формуле Дост = 1+ 3,322· lgN (2.1) Дост = 1 + 3,222 · lg50 = 6,643 мм2. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
