Практика по Excel. Учебная практика Excel. Отчет по учебной практике (технологическая (проектнотехнологическая) практика)
 Скачать 0.95 Mb. Скачать 0.95 Mb.
|
|
Челябинск 2020 год МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Челябинский государственный университет» (ФГБОУ ВО «ЧелГУ») Институт информационных технологий Кафедра информационных технологий и экономической информатики ОТЧЕТ ПО УЧЕБНОЙ ПРАКТИКЕ (ТЕХНОЛОГИЧЕСКАЯ (ПРОЕКТНО-ТЕХНОЛОГИЧЕСКАЯ) ПРАКТИКА) Сроки прохождения практики: 28.06.2021 -11.07.2021(дата начала практики – дата окончания практики) Выполнил студент группы(группа, ФИО, подпись) Руководитель практики НиколаевИ.Е.(ФИО) Оценка:(оценка, подпись, дата) Челябинск, 2021Оглавление: Задачи первого уровня 2 Задачи второго уровня 10 Задачи третьего уровня 19 Библиография Задачи первого уровня Количество учащихся на дополнительных курсах английского языка в университете с 2014 по 2020 годы отображено в таблице ниже. Таблица №1 – Кол-во учащихся на доп. курсах английского языка
По данным таблицы постройте диаграмму. Решение: Выбираем гистограмму с группировкой, результат – рис. 1 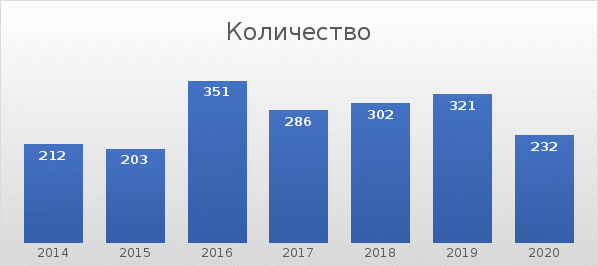 Рис. 1 – Кол-во учащихся на дополнительных курсах английского языка Сахарный тростник содержит 9% сахара. Сколько сахара будет получено из 20 тонн сахарного тростника? Решение: 20 т * 9/100 * 1000 кг = 1800 кг Преобразуем формулу для Excel =ПРОИЗВЕД(C4;G4/100)*1000, где С4 – это ячейка, в которой указано количество сахарного тростника, G4/100 – содержание сахара в сахарном тростнике в процентах, и множитель 1000 для получения результата в килограммах, Рис. 2 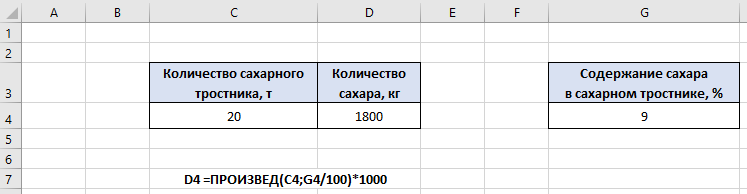 Рис. 2 – Содержание сахара в сахарном тростнике Определить сумму скидки в оплате товара, если стоимость покупки больше 20000 рублей, то скидка – 10%, если более 5000 рублей, то 5%, иначе скидка не предоставляется. Таблица №2 – Исходные данные 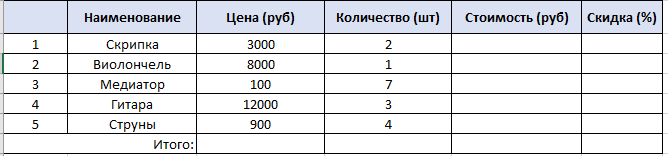 Рассчитайте сумму к оплате со скидкой и без скидки по каждому товару, а также по всем товарам вместе. Решение: все расчёты показаны на рис. 3 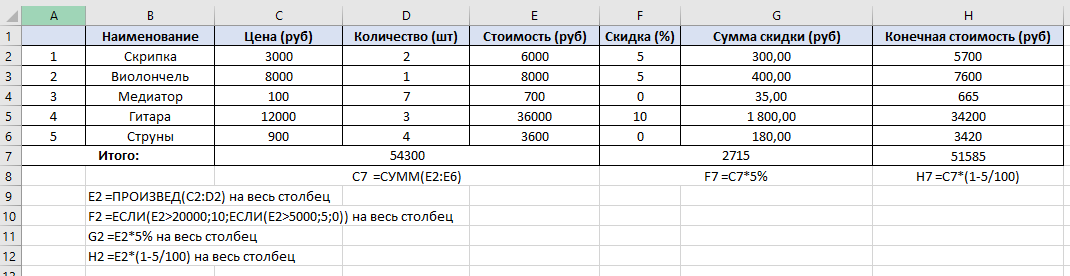 Рис. 3 «Расчёт скидки на товары» Постройте диаграмму объёма продаж спортивных костюмов разных торговых марок по кварталам по данным таблицы. Таблица №3 – Объём продаж по кварталам 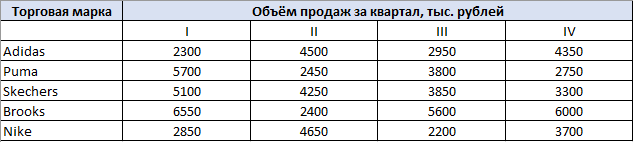 Рассчитайте: Годовой объём продаж; Среднее, Минимальное и Максимальное значения квартального объёма продаж. Решение: Годовой объём продаж =СУММ(B3:E3) Среднее значение =СРЗНАЧ(B3:E3) Минимальное значение =МИН(B3:E3) Максимальное значение =МАКС(B3:E3) Результат вычислений – столбцы F, G, H и I рис. 4, диаграмма – рис. 5 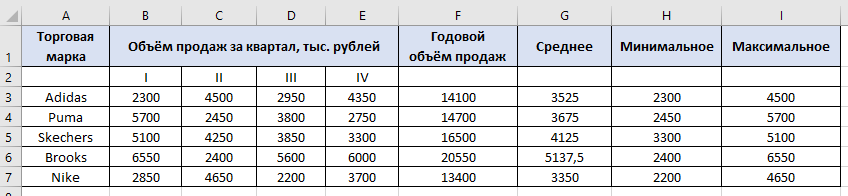 Рис. 4 – Объём продаж 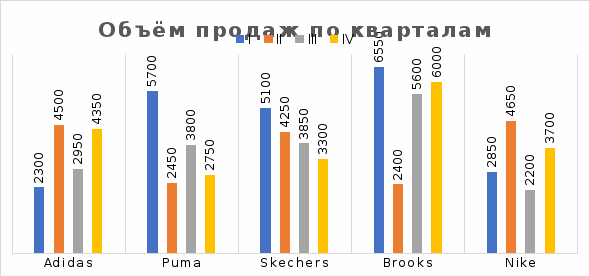 Рис. 5 – Диаграмма объёма продаж по кварталам В семье Ивановых 3 детей, Стрельниковых – 4 и Ложкиных – 2. Стоимость обеда в школе составляет 56 рублей. Рассчитайте затраты этих семей на школьные обеды в месяц, если дети учатся 6 дней в неделю. Постройте диаграмму, на которой будет отражена разница между затратами на школьные обеды трёх семей. Решение: составляем таблицу, вводим формулу для расчёта D3 =C3*56*6*4 протягиваем на весь столбец. 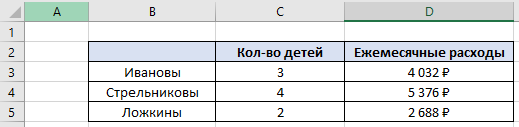 Рис. 6 – Ежемесячные расходы на питание По данной таблице строим диаграмму, рис. 7 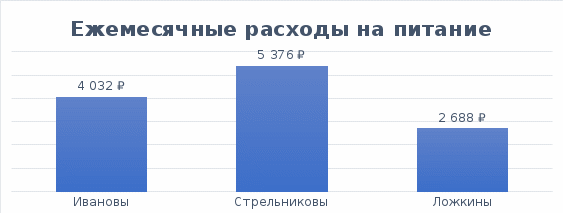 Рис. 7 – Диаграмма ежемесячных расходов на питание Численность населения города составляла: 1 января – 80500 чел., 1 февраля – 80540 чел., 1 марта – 80550 чел., 1 апреля – 80560 чел., 1 мая – 80575 чел., 1 июня – 80590 чел., 1 июля – 80620 чел., 1 августа – 80580 чел., 1 сентября – 80680 чел., 1 октября – 80685 чел., 1 ноября – 80690 чел., 1 декабря – 80705 чел., 1 января следующего года – 80730 чел. Определите среднюю численность населения: В четвёртом квартале В первом полугодии За год в целом Отобразите среднюю численность населения на диаграммах. При подсчётах учитывать данные на начало месяца. Решение: Средняя численность =СРЗНАЧ(C3:C15) IV квартал =СРЗНАЧ(C11:C14) 1-е полугодие =СРЗНАЧ(C3:C8) За год =СРЗНАЧ(C3:C14) Результат вычислений рис. 8, диаграмма – рис. 9 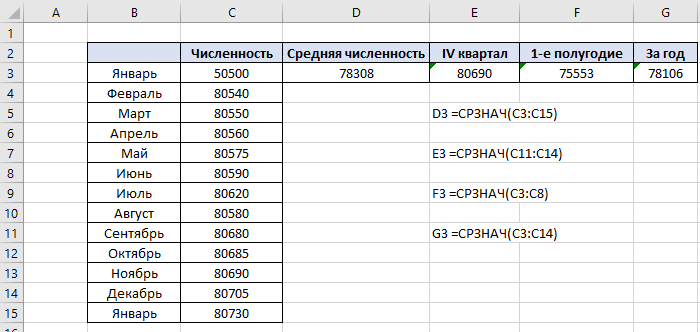 Рис. 8 – Среднее значение в разные периоды времени 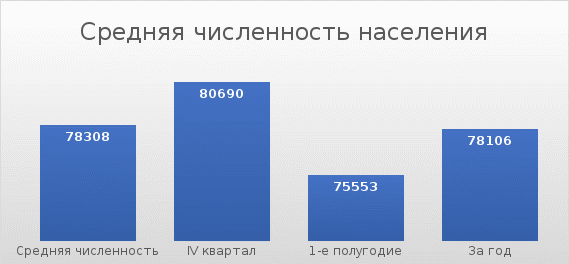 Рис. 9 – Средняя численность населения Один мастер может выполнить заказ за 12 часов, а другой – за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе? Решение: вся работа = 1, первый мастер = 1/12, второй мастер = 1/6, вместе мастера выполнят всю работу за 1/12 + 1/6 = 4 часа. Занесём все данные в таблицу и введём формулу в ячейку результата, рис. 10 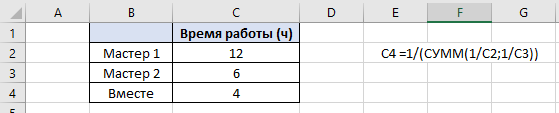 Рис. 10 – Расчёт совместной работы Найдите решение уравнения 4x^2-16x+10=0 Решение: при решении квадратных уравнений необходимо определить дискриминант, от его значения будет зависеть количество корней уравнения D > 0 уравнение имеет два корня D = 0 один корень D < 0 корней нет Дискриминант находится по формуле: D = b^2 - 4ac Корни х1 и х2 по формуле 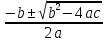 Создадим таблицы в Excel и вставим вышеприведённые формулы в соответствующие ячейки. Для дискриминанта добавляются условия равенства нулю, формула выглядит следующим образом: =ЕСЛИ(E5*E5-4*D5>0;">";ЕСЛИ(E5*E5-4*D5=0;"=";"<")) Для корней уравнения формула примет вид: Х1 =ЕСЛИ(I4=">";(-E5+КОРЕНЬ(E5^2-4*D5*F5))/(2*D5);ЕСЛИ(I4="=";-E5/2*D5;"Нет корня")) Х2 =ЕСЛИ(I4=">";(-E5+КОРЕНЬ(E5^2-4*D5*F5))/(2*D5);ЕСЛИ(I4="=";-E5/2*D5;"Нет корня")) В результате получим: х1 = 3,244, х2 = 0,775, как показано на рис. 11  Рис. 11 – Решение квадратного уравнения В таблице отображена стоимость товаров в у.е. различных компаний поставщиков. Продаётся 200 ед. товара 1, 300 ед. товара 2, 400 ед. товара 3, 500 ед. товара 4 и 600 ед. товара 5. Рассчитайте максимальное и минимальное значение выручки. Таблица №4 – Стоимость товаров 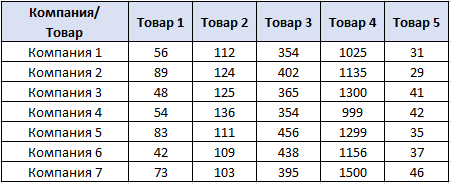 Постройте диаграмму выручки компаний по каждому проданному товару. Решение: Максимальная выручка =МАКС(D6:D12)*D14 Минимальная выручка =МИН(D6:D12)*D14 Результаты вычислений рис. 12, диаграмма – рис. 13 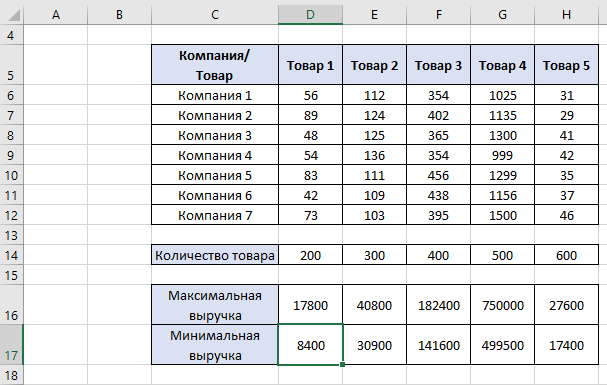 Рис. 12 – Выручка компаний по каждому товару 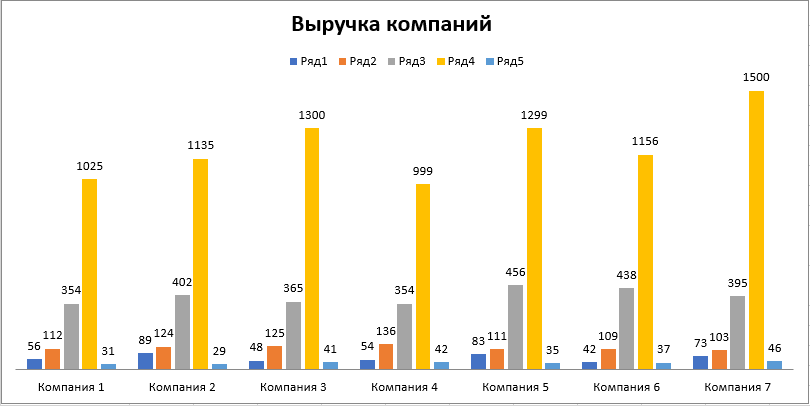 Рис. 13 Выручка компаний, диаграмма Рассчитайте сумму покупки каждой компании, учитывая, что цена для каждого товара зависит от его количества. 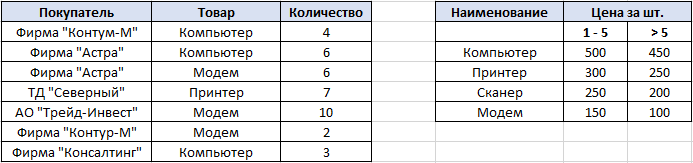 Рис. 14 – Количество товара и условие цены товара Решение: к таблице с исходными данными добавим столбец «Сумма», и с помощью формулы =ВПР(D14;G6:I9;ЕСЛИ(E14>5;3;2);0)*E14 вычислим стоимость каждого товара, для каждой компании с учётом скидок, если таковые имеются, рис. 15 В формуле для корректировки цены товара используется диапазон G5:I9, и в зависимости от количества товара, устанавливается его цена ЕСЛИ(E14>5;3;2), то есть если количество больше 5 штук, то значение выбирается из третьего столбца таблицы – I, если меньше – второго H, иначе скидки нет. Общие суммы покупок для каждой компании, занесены в отдельную таблицу, (столбцы K, L) и вычисляются по формуле: =СУММЕСЛИ(C14:C20;K5;F14:F20) Смысл формулы заключается в том, чтобы суммировать все значения из столбца F, диапазон F14:F20 (сумма покупки по каждому товару), лишь в том случае, если соответствующее значение из столбца С, диапазон C14:C20 (покупатель) совпадает с запрашиваемым покупателем по условию, например К5 – Фирма «Контур-М». 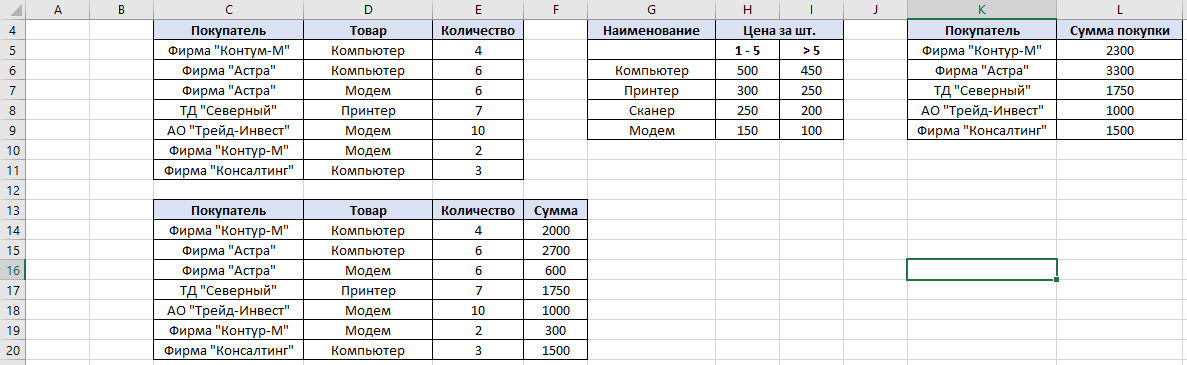 Рис. 15 – Расчёт суммы покупок Рассчитайте по всем товарам средние значения объёма партии, цены затрат и прибыли, а также суммарные значения объёма партии и прибыли. Решение: Сумма партий =СУММЕСЛИ($A$2:$A$15;I2;$C$2:$C$15) Сумма прибыли =СУММЕСЛИ($A$2:$A$15;I2;$F$2:$F$15) Средняя партия =СРЗНАЧЕСЛИ($A$2:$A$15;I2;$C$2:$C$15) Средняя цена =СРЗНАЧЕСЛИ($A$2:$A$15;I2;$D$2:$D$15) Средние затраты =СРЗНАЧЕСЛИ($A$2:$A$15;I2;$E$2:$E$15) Средняя прибыль =СРЗНАЧЕСЛИ($A$2:$A$15;I2;$F$2:$F$15) Особенностью данных формул является то, что из первого заданного диапазона значений $A$2:$A$15 выбираются только те значения, которые соответствуют условию, например I2 (Твикс) и во втором диапазоне, например $C$2:$C$15 (объём партии) складываются значения соответствующие выбранным из первого диапазона. Для фиксации диапазонов при поиске используются символы $, это необходимо, чтобы поиск всегда начинался с одной и той же строки, иначе для следующего заданного условия поиск будет сдвигаться на строку ниже и первые строки с данными не будут задействованы в расчёте. 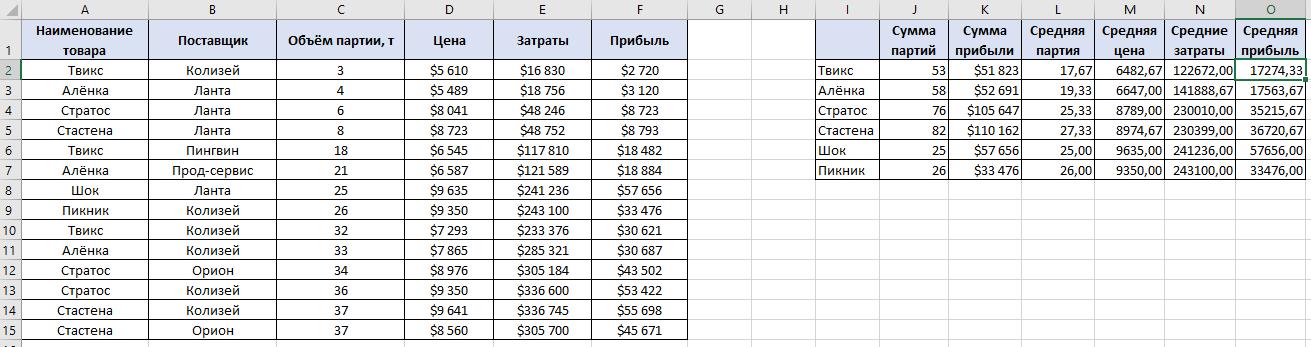 Рис. 16 – Средние значения объёма партии, цены и прибыли Составьте таблицы перерасчёта рублей в доллары и доллары в рубли, если курс на настоящий момент составляет 75 рублей. Предусмотрите возможность изменения курса доллара. Решение: Для перевода рубли в доллары =F4/D3 Для перевода доллары в рубли =F8*D3 Результат на рис. 17 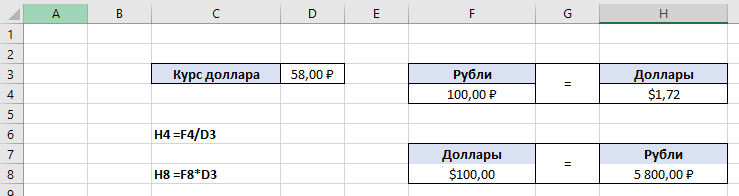 Рис. 17 – Курс доллара Задачи второго уровня Известны данные о годовых продажах литературы в трёх книжных магазинах. Показатели годовых продаж в тыс. рублей отображены в таблице №5. Таблица №5 – Показатели годовых продаж  По данным таблицы необходимо построить различные типы диаграмм: Суммарные продажи литературы по всем книжным магазинам; Доли годовых продаж литературы в книжных магазинах; Продажи каждого жанра литературы в каждом книжном магазине. Решение: Диаграмму по продажам каждого жанра литературы в каждом книжном магазине строим по таблице с исходными данными, таблица №5, результат – рис. 18 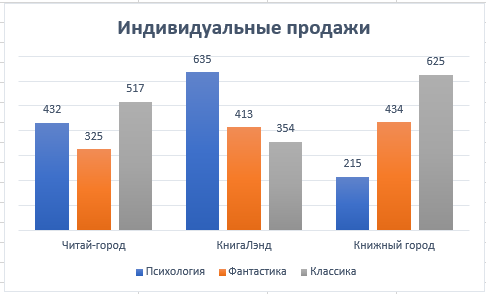 Рис. 18 – Индивидуальные продажи по жанрам Для построения диаграмм суммарных и годовых продаж, создаём дополнительную таблицу, рис. 19 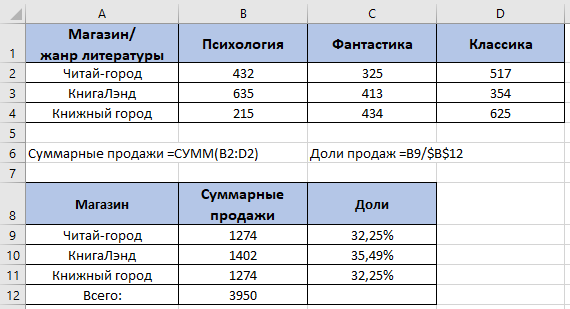 Рис. 19 – Расчёт Суммарных и годовых продаж Где сумма всех продаж =СУММ(B9:B11); Суммарные продажи =СУММ(B2:D2); Доли продаж =B9/$B$12. Диаграммы представлены на рис. 20 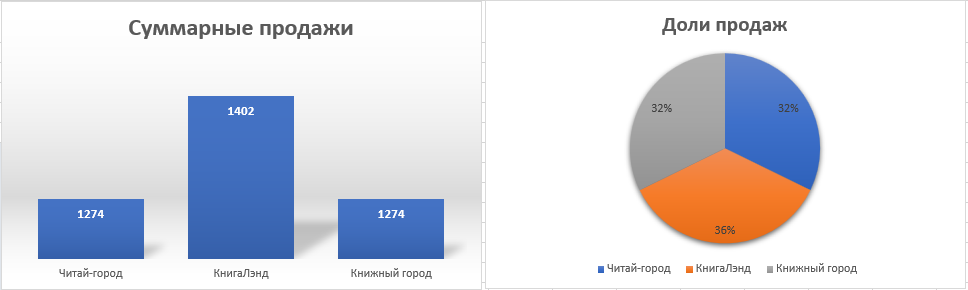 Рис. 20 – Суммарные продажи и доли продаж каждого магазина Известны данные о рабочих часах в неделю сотрудников организации «Мир». Установленный график работы сотрудников 5/2 по 8 часов и 2/2 по 12 часов, рис. 21 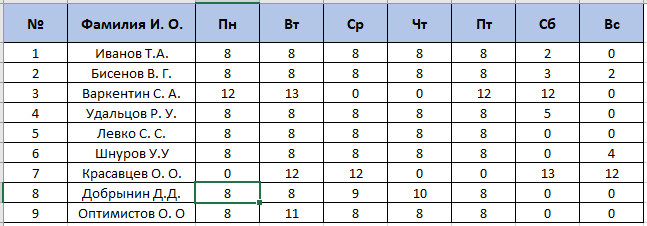 Рис. 21 – График работы сотрудников организации «Мир» Рассчитайте: Заработную плату каждого сотрудника за неделю (с учётом переработки); Суммарную выплату з/п в неделю всем сотрудникам (с учётом переработки) Оплата по установленному графику составляет 1300 рублей в час, а каждый час переработки оплачивается в двойном размере. Решение: для решения задачи создадим дополнительную таблицу, рис. 22, столбцы K, L, M, которая будет состоять из списка всех сотрудников и их з/п за неделю. 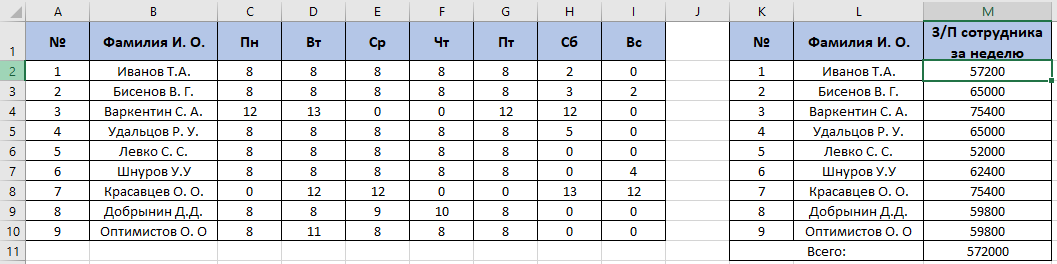 Рис. 22 – Расчёт з/п сотрудников за неделю Заработная плата сотрудника состоит из двух частей: фактически отработанные часы и сверхурочные, которые оплачиваются в двойном размере =СУММ(C2:I2)*1300+(СУММ(C2:I2)-40)*1300, где СУММ(C2:I2)*1300 – время отработанное по графику (СУММ(C2:I2)-40)*1300 – сверхурочные Суммарная выплата находится по формуле =СУММ(M2:M10), ячейка М11 и составит 57200 рублей. Постройте график функции у = kx + b для х в диапазоне от -10 до 10 с шагом 0,5, k и b – произвольные. Решение: k = 7, b = 3, далее строим таблицу значений х и у, рис. 23 где х – от минимального по условию нарастает с градацией 0,5 формула =B10+$C$5, начиная со второй строки В11. Значение yвычисляется по формуле =$A$5*B11+$B$5. 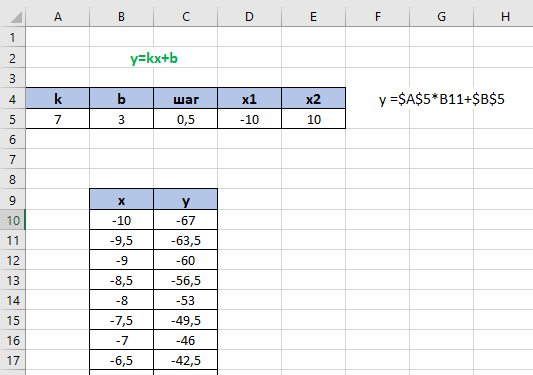 Рис. 23 – Вычисление значений для x и y По данным получившейся таблицы строим график, рис. 24 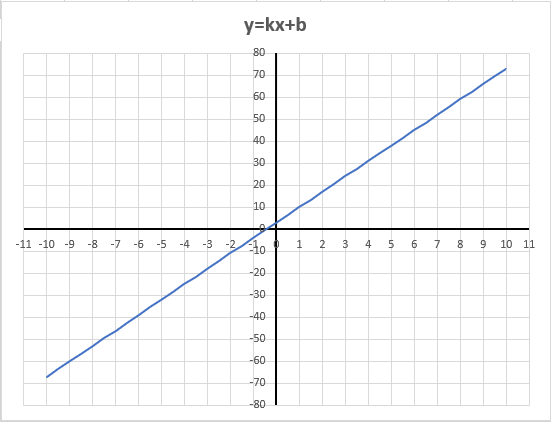 Рис. 24 – График функции у = kx + b Два друга Рома и Паша положили в банк по 100 000 рублей на три года под 10% годовых. Однако через год и Рома, и Паша сняли со своих счетов соответственно 10% и 15% имеющихся денег. Ещё через год каждый из них снял со своего счёта соответственно 15 000 рублей и 10 000 рублей. Рассчитайте, у кого из друзей к концу третьего года на счету окажется большая сумма денег? Постройте диаграмму, на которой будет отображено изменение денежных сумм на счетах у двух друзей в банке на протяжении 3 лет. Решение: строим таблицу для расчёта, рис. 25  Рис. 25 – Изменение денежных средств за 3 года Дебет =B4-C4+D4, Остаток на конец года =E4+E4*10/100 Расход на второй год для Ромы составил 10%, это =G4*10/100, 11 000 рублей. Для Паши 15% – это =G5*15/100, 16 500 рублей. На третий год Рома снял 15 000 рублей, а Паша 10 000 рублей, что также отображено в таблице. Для построения диаграммы добавим сводную таблицу, рис. 26, по данным которой построим диаграмму изменения денежных средств, рис. 27  Рис. 26 – Сводная таблица расходов 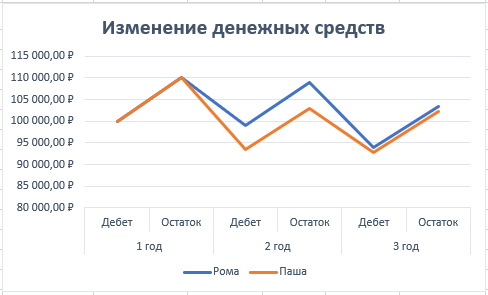 Рис. 27 – Диаграмма изменения денежных средств В заключение расчёта можно сказать, что к концу 3 года остаток денежных средств на счету у Ромы составил 103 290 рублей, что на 1155 рублей больше, чем у Паши, остаток денежных средств которого составил 102 135 рублей. Создать таблицу расчёта оптимального веса для человека. Столбец «Оптимальный вес» вычисляется по формуле: Для мужчин: Оптимальный вес = (Рост – 100) * 1,15 Для женщин: Оптимальный вес = (Рост – 110) * 1,15 Если вес человека оптимальный, то в столбце «Советы», напротив его фамилии, должна появиться запись «Оптимальный вес». Если вес меньше оптимального – «Вам нужно поправиться на», с указанием в соседней ячейке количества недостающих килограмм. Если вес больше оптимального – «Вам нужно похудеть на» с указанием в соседней ячейке количества лишних килограмм. Решение: Для расчёта оптимального веса, в столбец Е введём заданную формулу =(D3-100)*1,15 для мужчин и =(D7-110)*1,15 – для женщин, рис 28 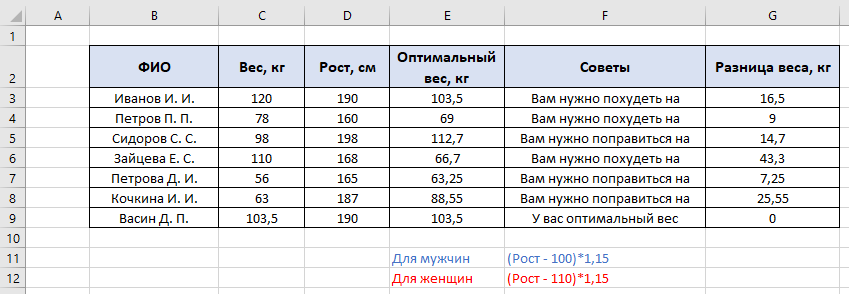 Рис. 28 – Расчёт оптимального веса Чтобы получить соответствующий совет, для столбца F зададим условие: =ЕСЛИ(C3=E3;"У вас оптимальный вес";ЕСЛИ(C3>E3;"Вам нужно похудеть на";"Вам нужно поправиться на")) Для расчёта разницы веса =ЕСЛИ(C3=E3;0;ABS(C3-E3)). Определите, какое количество ноутбуков, принтеров и сканеров было продано каждому клиенту за все годы сотрудничества, таблица №5. Определите суммарные стоимости каждого вида товара за все годы. По данным отчёта построить соответствующие диаграммы. Таблица №5 – Отчёт по проданным товарам за все годы сотрудничества
Решение: Для расчёта строим таблицу по запрашиваемым по условию товарам, рис. 29 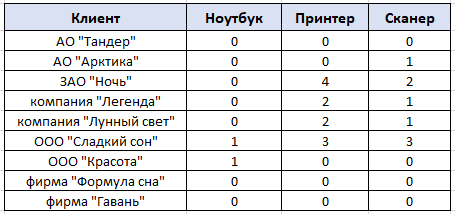 Рис. 29 – Количество товаров Чтобы подсчитать количество товаров по каждому клиенту запишем формулу в каждый столбец с наименованием товара: Ноутбук =СУММЕСЛИМН($C$4:$C$54;$B$4:$B$54;$I$3;$E$4:$E$54;H4), Принтер =СУММЕСЛИМН($C$4:$C$54;$B$4:$B$54;$J$3;$E$4:$E$54;H4) Сканер =СУММЕСЛИМН($C$4:$C$54;$B$4:$B$54;$K$3;$E$4:$E$54;H4) Смысл формулы СУММЕСЛИМН заключается в поиске нескольких значений по условию среди нескольких диапазонов. Например, значение «ноутбук» находится в диапазоне названий товаров сводной таблицы (исходные данные), если имя клиента совпадает с заданным по условию, то соответствующие значения в столбце «количество» складываются. По данным таблицы, рис. 29 строим диаграмму, рис. 30 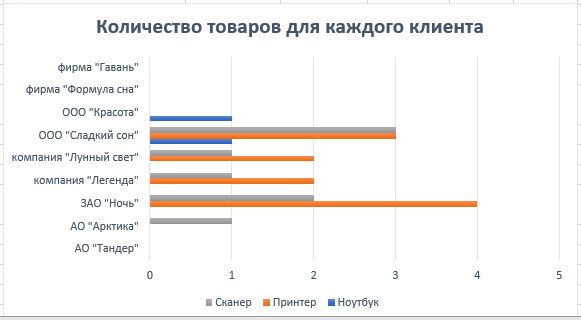 Рис. 30 – Статистика по трём товарам для каждого клиента Для расчёта суммарной стоимости также строится дополнительная таблица, рис. 31 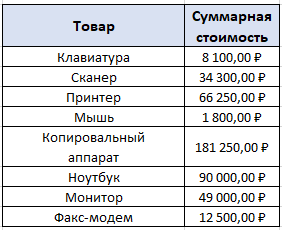 Рис. 31 – Суммарная стоимость покупок Используется формула =СУММЕСЛИ($B$4:$B$54;H16;$D$4:$D$54), смысл которой заключается в сложении значений из столбца «Сумма», таблицы с исходными данными, в том случае, если название товара в столбце «Наименование», той же таблице с исходными данными, совпадает с заданным по условию значением, например «Клавиатура». По данным таблицы, рис. 31 строим диаграмму, рис. 32 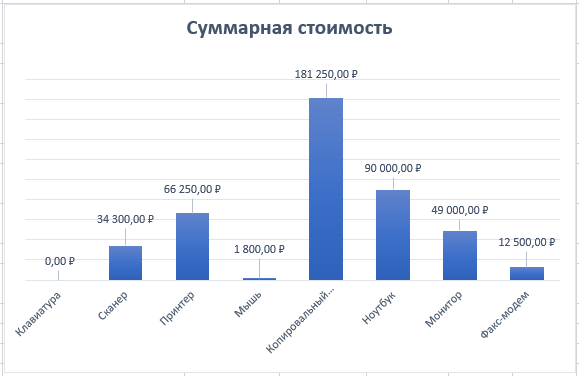 Рис. 32 – Суммарная стоимость по каждому товару Постройте смешанную диаграмму по таблице «Данные отделений банка Финанс», таблица №6. Постройте диаграмму с отображением итоговых значений по каждому отделению по таблице «Выдано Master Card», таблица №7. Таблица №6 – Данные отделения банка «Финанс» 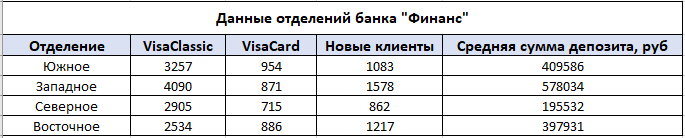 Таблица №7 – Выдано «Master Card» 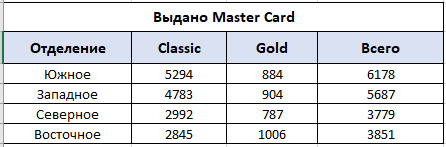 Решение: для каждой таблицы с данными выбираем комбинированные диаграммы, результат рис. 33 и рис. 34 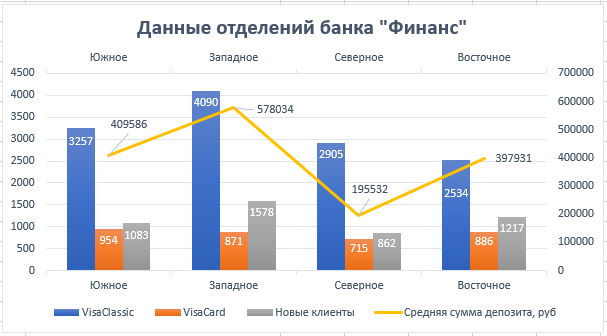 Рис. 33 – Данные отделений банка «Финанс» 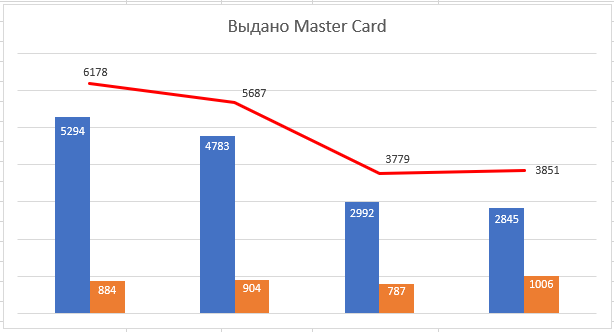 Рис. 34 – Выдано «Master Card» Задачи третьего уровня Постройте диаграмму Ганта на базе данных этапов разработки дизайн проекта, рис. 35 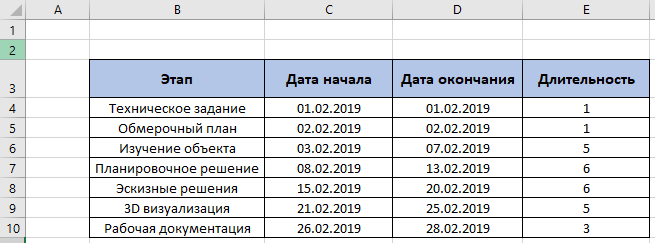 Рис. 35 – Длительность этапов разработки Для расчёта длительности используем формулу =D4-C4+1 Затем выбираем линейчатый тип диаграммы и корректируем её до получения соответствующего, более наглядного вида, рис.36 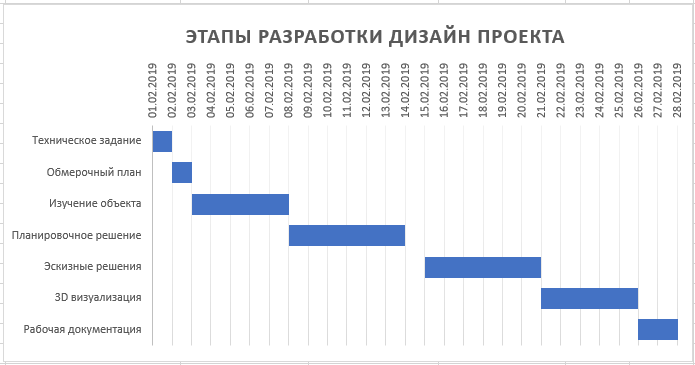 Рис. 36 – Этапы разработки дизайн проекта Транспортная задача 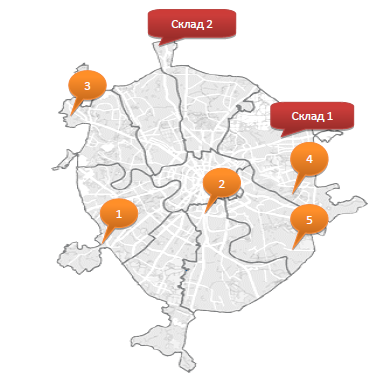 Рис. 37 – Распределение товаров Распределите доставку товара в 5 магазинов с 2-х складов таким образом, чтобы затраты на доставку были минимальны. При этом необходимо учесть требуемое количество единиц товара в каждый из магазинов и ёмкость каждого склада. Ёмкость склада 1 составляет 800 ед. товара, 2 склада – 700 ед. товара. Данные по стоимости доставки товара в магазины (руб. за ед. товара) и потребности каждого магазина приведены в таблице №8. Таблица №8 – Данные по каждому магазину  Решение: для решения задачи создадим идентичную таблицу, рис. 39, но данные по расходам вычислим с помощью встроенного в Excel средства анализа данных. 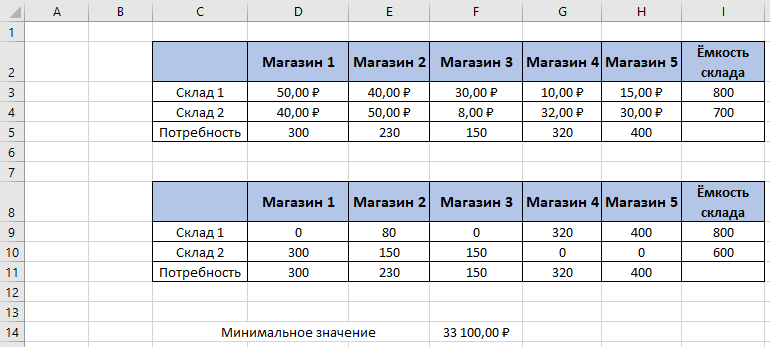 Рис. 39 – Решение транспортной задачи Для расчёта минимального значения выбираем произвольную ячейку, например F14, куда запишем формулу =СУММПРОИЗВ(D9:H10;D3:H4), где по двум диапазонам будет вычисляться минимальное значение транспортного расхода, а во второй таблице появятся соответствующие значения – количество единиц товара для каждого магазина в зависимости от его потребности и ёмкости склада. Выделяем ячейку F14, куда записана формула, затем на вкладке «Данные», в группе команд «Анализ» выбираем пункт «Поиск решения», рис. 40  Рис. 40 – Поиск решения Далее работаем с окном параметров, рис. 41 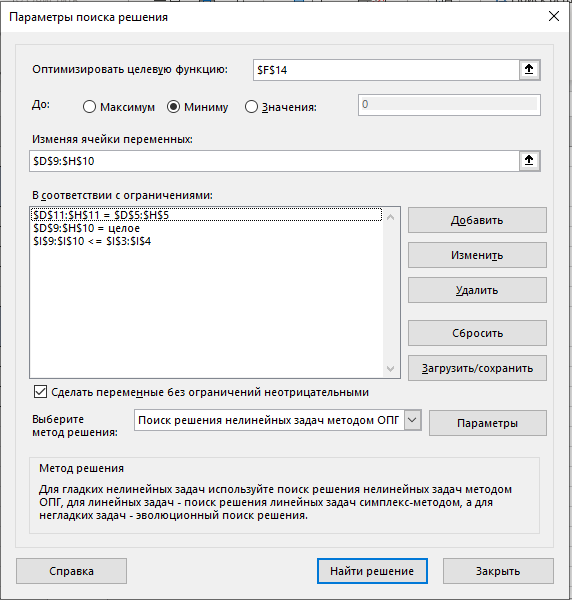 Рис. 41 – Окно параметров Здесь указываем: «Оптимизировать целевую функцию до минимума», диапазон, в ячейках которого мы ходим изменить данные – это $D$9:$H$10. Добавляем ограничения: Полученные значения должны быть целым числом (ед. товара) $D$9:$H$10 = целое Потребности в товаре исходных данных и расчётных должны быть равны $D$11:$H$11 = $D$5:$H$5 Ёмкость склада расчётная должна быть меньше или равна действительной $I$9:$I$10 <= $I$3:$I$4 Добавив все вышеперечисленные условия, запускаем поиск решения, результат – рис. 39 Минимальные затраты на доставку 33 100 рублей. Создайте сводную таблицу по данным таблицы №9 и отобразите в ней общую площадь, общее число жителей и общую плотность населения для каждого полушария. Таблица №9 – Данные по Западному и Восточному полушарию 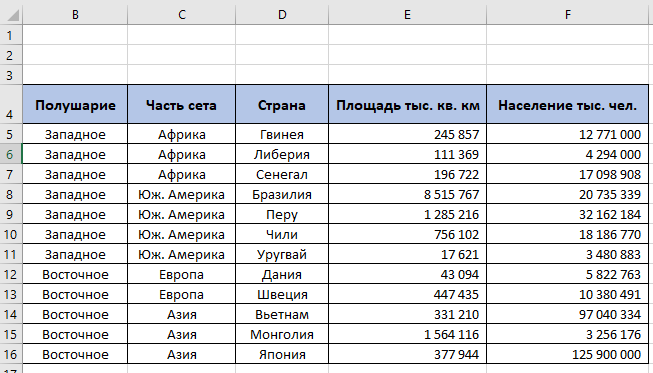 Решение: Создадим новую таблицу для подсчёта требуемых данных, рис. 42 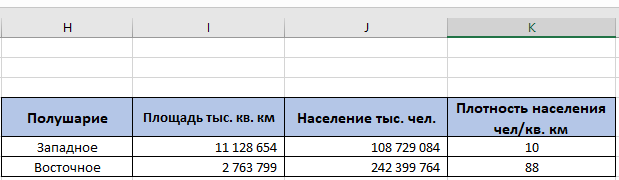 Рис. 42 – Общие данные по двум полушариям Земли Площадь Западного полушария = 11 128 654 тыс. кв. км – это сумма площади всех стран, относящихся к Западному полушарию, рассчитывается по формуле =СУММ($E$5:$E$11). Аналогично рассчитывается площадь Восточного полушария = 242 399 764 тыс. кв. км, формула =СУММ($E$12:$E$16). Население Западного полушария = 108 729 084 тыс. чел. – это сумма населения стран западного полушария из таблицы №9. Формула =СУММ($F$5:$F$11). Население Восточного полушария = 242 399 764 тыс. чел. Формула =СУММ($F$12:$F$16). Плотность населения – это результат деления население / площадь по таблице, рис. 42. Для Западного полушария 10 чел/кв. км, формула =J5/I5. Для Восточного полушария 88 чел/кв. км, формула =J6/I6 Спрогнозируйте данные на 2021 год на основе имеющихся. Постройте график, показывающий изменение продаж погодам, рис. 43 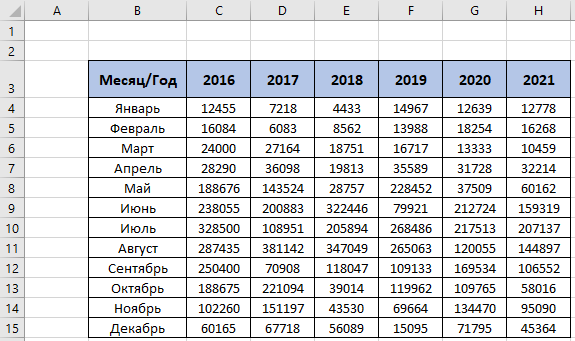 Рис. 43 – Изменение продаж по годам Решение: Для прогнозирования продаж на 2021 год используем формулу =ПРЕДСКАЗ($H$3;C4:G4;$C$3:$G$3), которая рассчитывает (или прогнозирует) будущее значение на линейном тренде, на основании имеющихся значений, результат – рис. 43. Далее на основании полученных данных строим диаграмму, рис. 44 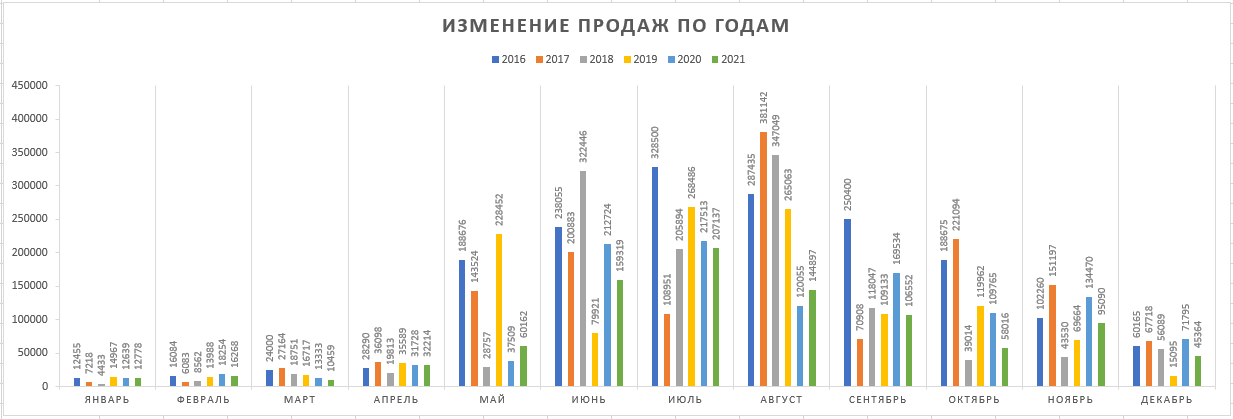 Рис. – Изменение продаж по годам Список литературы |
