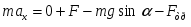Отсчета. Способы описания движения. Кинематические характеристики движения точки. Траектория. Путь. Перемещение. Скорость. Мгновенная и средняя скорость. Ускорение
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
|
6. Относительность движения. Преобразование Галилея для координат, скоростей, ускорений, массы, силы. Принцип относительности Галилея. Относительность движения проявляется в том, что скорость, траектория, пройденный путь и некоторые другие характеристики движения относительны, то есть они могут быть различны в различны в разных системах отсчета . Принцип относительности Галилея: во всех инерциальных системах отсчета одни и те же механические явления протекают одинаково, при этом законы динамики, описывающие эти явления одинаковы. Поэтому все инерциальные системы отсчета эквивалентны, т. е. равноправны. Рассмотрим две системы отсчета: неподвижную (К) и движущуюся относительно первой вдоль оси Х с постоянной Х с постоянной скоростью (K’). Координаты тела М в системе К x:y:z , а в системе К’ - x’: y’: z’. Эти координаты связаны между собой соотношениями, которые называются преобразованиями Галилея 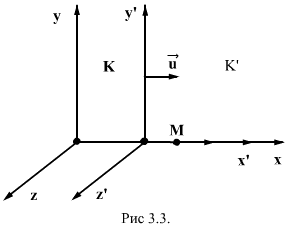 Дифференцируя эти уравнения по времени и учитывая, что , найдем соотношения между скоростями и ускорениями:
Таким образом, если в системе К тело имеет ускорение а, то такое же ускорение оно имеет и в системе К’. Согласно второму закону Ньютона: т.е. второй закон Ньютона одинаков в обоих случаях. При движение по инерции, т.о., справедлив и первый закон Ньютона, т.е. рассматриваемая нами подвижная система является инерциальной. Следовательно, уравнения Ньютона для материальной точки инвариантны по отношению к преобразованиям Галилея. Этот результат называется механическим принципом относительности (принцип относительности Галилея). 7. Динамика материальной точки. Инерциальные системы отсчета. Законы Ньютона. Алгоритм решения задач на законы Ньютона. Динамика – раздел механики, изучающий движение тела(материальной точки) и причины, вызывающие его. Основу динамики составляют законы Ньютона. Первый закон Ньютона: всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока и поскольку воздействие со стороны других тел не понуждает его изменить это состояние. Явление сохранения телами состояния покоя или равномерного прямолинейного движения называют инерцией. Свойства тел сохранять свое состояние - инертность, а система отсчета – инерциальная. Сила – воздействие на тело со стороны других тел. Масса – мера инертности тела. Второй закон Ньютон: Ускорение ,приобретаемое телом, прямо пропорционально приложенной силе и обратно пропорционально массе тела. 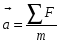 Произведение массы тела на его ускорение равно приложенной силе. 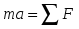 Третий закон Ньютона: Действию всегда соответствует равное и противоположное противодействие. Силы, с которыми тела взаимодействуют между собой, равны по модулю, но противоположны по направлению. 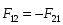 Алгоритм решения(2 Закон Ньютона):  -? -?a m 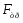 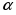
8. Понятие о системах материальных точек. Замкнутые и незамкнутые системы. Импульс тела. Импульс системы материальных точек. Второй закон Ньютона для системы материальных точек. Система материальных точек – система, состоящая из совокупности тел, размеры и форма которых не играют роли на характер движения. В системе материальных точек на каждую из них будет действовать совокупность сил со стороны системы. Эти силы называют внутренними. Если на систему происходит воздействие со стороны тел, не входящих в систему, то это внешние силы. Замкнутая система – это система, в которой можно пренебречь воздействием внешних сил. Незамкнутая система – это система, для которой характерно множество внешних воздействий. Импульс тела – физическая величина, измеряемая произведением массы тела на скорость его движения 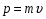 Импульс замкнутой системы материальных точек есть величина постоянная, или, другими словами, в отсутствие внешних сил сумма импульсов всех точек системы остается постоянной, какие бы изменения внутри системы ни происходили. P=const. В отсутствие сил импульс материальной точки сохраняется неизменным по модулю и направлению. 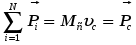  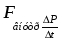 = 0 = 0 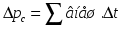 9. Движение тел с переменной массой. Вывод уравнения Мещерского. Реактивное движение. Формула Циолковского. Реактивное движение – это движение, возникающее при изменении массы движущегося тела в случае отделения или прибавления частей с некоторой скоростью. m(t) Реактивная сила – сила реакции отбрасываемого тела. 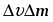 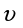 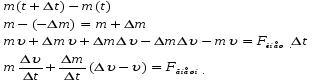 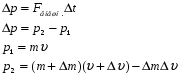 Уравнение Мещерского: Формула Циолковского: 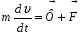 (Ф – реактивная сила) (Ф – реактивная сила) 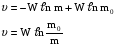 (  - начальная масса ракеты, m – конечная масса ракеты, W= - начальная масса ракеты, m – конечная масса ракеты, W= 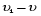 ) )10.Сила, ее свойства и способы измерения. Сила – векторная физическая величина, являющаяся мерой интенсивности взаимодействия тел. Приложенная к массивному телу, сила является причиной изменения его скорости или возникновения в нем деформаций. Сила, как векторная величина, характеризуется модулем и направлением. Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение движения материальной точки совпадает по направлению с приложенной силой; по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, в инерциальных системах отсчета скорость изменения импульса материальной точки равна приложенной силе. Деформация является следствием возникновения в теле внутренних напряжений. В механике силы обладают тремя основными свойствами, называемыми законами Ньютона. Возможны два пути измерения силы: а) по деформации эталонного тела (напр., пружины); б) по ускорению эталонного тела. Силы в природе: Гравитационные Электромагнитные Сильные (ядерные) Слабые Консервативные и диссипативные силы. Консервативными силами называются силы, работа которых не зависит от пути перехода тела или системы из начального положения в конечное. Характерное свойство таких сил – работа на замкнутой траектории равна нулю: К консервативным силам относятся: сила тяжести, гравитационная сила, сила упругости и другие силы. Неконсервативными(диссипативными) силами называются силы, работа которых зависит от пути перехода тела или системы из начального положения в конечное. Работа этих сил на замкнутой траектории отлична от нуля. К неконсервативным силам относятся: сила трения, сила тяги и другие силы. Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, — консервативными. Равнодействующая сила – это сила, действие которой заменяет действие всех сил, приложенных к телу. Или, другими словами, равнодействующая всех сил, приложенных к телу, равна векторной сумме этих сил. 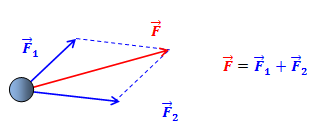 Третий закон Ньютона, использование закона для решения задач. При решении задач на третий закон Ньютона целесообразно использовать формулировку, в которой явно говорится о силах взаимодействия тел: силы, с которыми два тела действуют друг на друга, всегда равны по величине и противоположны по направлению. При этом необходимо обратить внимание на формирование следующих понятий. 1. Силы всегда возникают парами. Если есть одна сила, то есть и другая, ей противоположная. 2. Силы приложены к различным телам и поэтому не имеют равнодействующей. 3. Третий закон Ньютона ничего не говорит о результатах действия сил. Об этом говорит второй закон Ньютона. Если мы рассматриваем оба взаимодействующих тела как одну систему, то силы взаимодействия будут внутренними и потому не смогут изменить положение системы в целом. Задачи решают по одной схеме: находят равные и противоположно направленные силы, с которыми действуют друг на друга тела; рассматривают каждое тело в отдельности и, учитывая все действующие на него силы, определяют, что произойдет с рассматриваемым телом: изменится ли его движение, возникнет деформация и т. д. 11.Работа постоянной и переменной силы.     Мощность. Кинетическая энергия – это энергия движения. Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела: Теорема о кинетической энергии: работа приложенной к телу равнодействующей силы равна изменению его кинетической энергии: А=Ек2-Ек1. Если начальная скорость движения тела массой m равна нулю и тело увеличивает свою скорость до значения v, то работа силы равна конечному значению кинематической энергии тела. Кинетическая энергия и импульс тела. Импульсом тела называется векторная физическая величина, равная произведению массы тела на его скорость. Закон сохранения импульса – в замкнутой системе геометрическая сумма импульсов тел остается постоянной при любых взаимодействиях этой системы между собой. m1v1+m2v2= m1v1’+m2v2’. 12.Консервативные и неконсервативные силы системы. (было выше) Потенциальная энергия это энергия взаимодействия тел, либо частей тела, между собой. В потенциальном поле консервативных сил. Она зависит от расстояния, на котором находятся тела, и не зависит от их скорости. Таким образом, потенциальная энергия это скалярная величина, имеющая числовое значение, но не имеющая вектора направления. Также она способна совершать работу под действием сил поля. Изменение потенциальной энергии. A = –(Ep2 – Ep1). Связь силы и потенциальной энергии на примерах упругой и гравитационной силы. НЕ СДЕЛАНО Закон сохранения энергии: энергия никогда не исчезает и не появляется из ничего; она лишь превращается из одного вида в другой. ИЛИ Полная энергия (сумма кинетической и потенциальной энергии) изолированной системы, в которой действуют только консервативные силы, есть величина постоянная, какие бы механические изменения не происходили внутри системы. 13.Упругий и неупругий удар. Применение законов сохранения импульса и энергии к абсолютно упругому и абсолютно неупругому удару. При соударение шаров силы взаимодействия довольно резко изменяются с расстоянием между центрами масс, весь процесс взаимодействия протекает в очень малом пространстве и в очень короткий промежуток времени. Такое взаимодействие называют ударом. Различают два вида ударов: если тела являются абсолютно упругими, то удар называют абсолютно упругим. Если же тела абсолютно неупругие, то удар абсолютно неупругий. В данной лабораторной работе мы будем рассматривать только центральный удар, то есть удар, который происходит по линии, соединяющий центы шаров. Рассмотрим абсолютно неупругий удар. Этот удар можно наблюдать на двух свинцовых или восковых шарах, подвешенных на нити одинаковой длинны. Процесс соударения протекает следующим образом. Как только шары А и В придут в соприкосновение, начнется их деформация, в результате которой возникнут силы сопротивления (вязкое трение), затормаживающие шар А и ускоряющие шар В. Так как эти силы пропорциональны скорости изменения деформации (т. е. относительной скорости движения шаров), то по мере уменьшения относительной скорости они убывают и обращаются в нуль, как только скорости шаров выровняться. С этого момента шары, «слившись», движутся вместе. 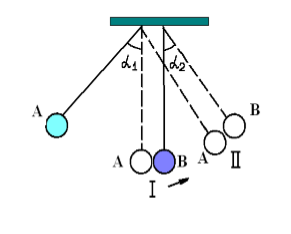 Рассмотрим задачу о ударе неупругих шаров количественно. Будем считать, что на них ни какие третьи тела не действуют. Тогда шары образуют замкнутую систему, в которой можно применить законы сохранения энергии и импульса. Однако силы действующие на них не консервативны. Поэтому к системе применим закон сохранения энергии: (1) где А- работа не упругих (консервативных) сил; E и E′ – полная энергия двух шаров соответственно до и после удара, состоящая из кинетической энергии обоих шаров и потенциальной энергии их взаимодействия между собой: Так как до и после удара шары не взаимодействуют, то Или Где массы шаров; - их скорости до соударения; v′ - скорость шаров после удара. Поскольку A<0, то равенство (3) показывает, что кинетическая энергия системы уменьшилась. Деформация и нагрев шаров произошли за счет убыли кинетической энергии. Для определения конечной скорости шаров следует воспользоваться законом сохранения импульса Так как удар центральный, то все векторы скоростей лежат на одной прямой. Принимая эту прямую за ость X и проецируя уравнение (5) на эту ось, получим скалярное уравнение: Из этого видно, что если шары до удара двигались в одну сторону, то после удара они будут двигаться в ту же сторону. Если же шары до удара двигались навстречу друг другу то после удара они будут двигаться в ту сторону, куда двигался шар, имеющий больший импульс. Поставим v′ из (6), в равенство (4): Таким образом, работа внутренних неконсервативных сил при деформации шаров пропорциональна квадрату относительной скорости шаров. |