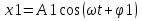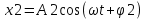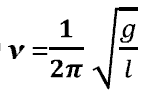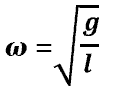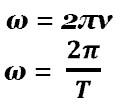Отсчета. Способы описания движения. Кинематические характеристики движения точки. Траектория. Путь. Перемещение. Скорость. Мгновенная и средняя скорость. Ускорение
 Скачать 1.75 Mb. Скачать 1.75 Mb.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| | 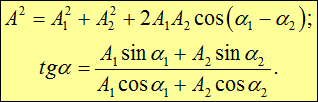 |
Колебания физического маятника. Вывод дифференциального уравнения движения. Анализ его решения. Частота и период колебаний физического маятника.
| M = I×e, | (1) |
| | . | (2) |
| | М = -mgℓsinq » -mgℓq, | (3) |
| | . | (4) |
| | . | (5) |
| | . | (6) |
| | . | (7) |
| | . | (8) |
Гармонический осциллятор. Энергия гармонического осциллятора.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
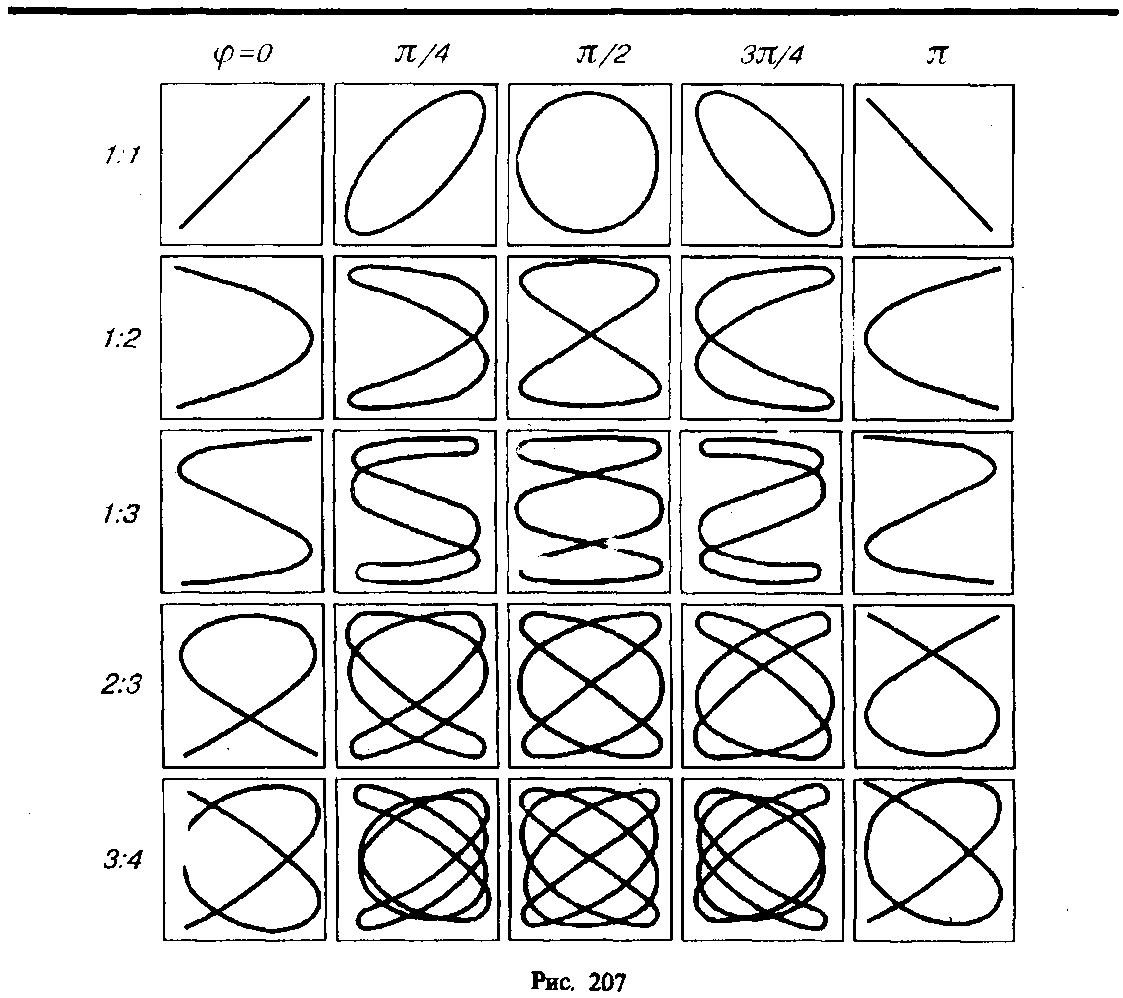
где - постоянная положительная величина, называют гармоническим осциллятором (или гармоническим вибратором). Как мы уже знаем, решение уравнения (1) имеет вид:
Следовательно, гармонический осциллятор представляет собой систему, которая совершает гармонические колебания около положения равновесия. В соответствии с 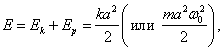 /2 есть полная энергия осциллятора; /2 есть полная энергия осциллятора; величина 2π/ω0 равна 1/υ0, где υ0 — собственная частота осциллятора, являющаяся для данного осциллятора величиной постоянной. Следовательно, площадь эллипса может быть представлена в виде Откуда
Таким образом, полная энергия гармонического осциллятора пропорциональна площади эллипса, причем коэффициентом пропорциональности служит собственная частота осциллятора. Площадь эллипса может быть вычислена как интеграл pdx. Поэтому формуле (64.5) можно придать следующий вид: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Затухающие колебания, дифференциальное уравнение затухающих колебаний. Зависимость амплитуды затухающих колебаний от времени. Характеристики затухающих колебаний: коэффициент затухания, логарифмический декремент затухания, добротность.
Любые свободные колебания являются затухающими, так как на систему всегда будет действовать сила сопротивления. Fсопр=-rυ(r-коэф сопротивления) ma=-kx-rυ. β=r/2m- коэф. затух.
d2x - kx + 2β dx = 0
dt2 m dt (дифференциальное уравнение затухающих колебаний + сопротивление среды.)
Если β большой, то результатом данного уравнения является уравнение: x=A0e-βtcos(ωt+φ0).
Зависимость амплитуды затухающих колебаний от времени из соотношения x=A0e-δtsin(ωt+φ0) видно, что в результате совместного действия квазиупругих сил f=-kx и сил трения fтр=-rυ система совершает колебательное движение, амплитуды А=А0е-δt убывает с течением времени по экспоненциальному закону; другими словами в системе возникают затухающие колебания.
Коэффициент затухания δ характеризует быстроту затухания колебаний. Затухающие колебания при строгом рассмотрении не являются периодическими. Поэтому о периоде затухаюших колебаний можно гово рить, когда β мало.
Если затухания выражены слабо (β→0), то
рассматривать как гармонические колебания, амплитуда которых меняется по экспоненциальному закону
Логарифмический декремент затухания - величина, равная натуральному логарифму двух последовательных амплитуд, разделённых промежутком времени, равным периоду.
θ =
Добротность. Энергетически колебательная система характеризуется добротностью. Добротность – увеличенное в 2π раз отношение полной энергии системы Е к энергии W рассеянной за период: Q=2π*(E/W). Чем меньше энергии рассеивается, тем больше добротность системы. Добротность обратно пропорциональна логарифмическому декременту. Добротность Q колебательной системы является мерой относительной рассеивания энергии. Добротность Q колебательной системы называется число, показывающее во сколько раз сила упругости больше силы сопротивления.
Вынужденные колебания. Дифференциальное уравнение вынужденных колебаний. Амплитуда вынужденных колебаний. Частота вынужденных колебаний. Резонанс.
Вынужденными называют такие колебания, которые возникают в колебательной системе при действии на неё внешней периодически изменяющейся силы, называемой вынуждающей силой.
Дифференциальное уравнение вынужденных колебаний.
d2x+kx+2βdx+F0cosωt = 0; x=x1+x2
dt2 m dt x=x1+x2 (x1-решение неоднородного уравнения гармонического колебания, х2-частное решение) x=A0cos(ωt+φ0)
Амплитуда вынужденных колебаний. Амплитуда зависит от соотношения частоты свободных колебаний (ω0) к (ω1). Амплитуда зависит также от F0 и коэффициента затухания δ.
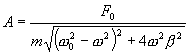
Частота вынужденных колебаний (вынуждающая частота) зависит от частоты изменения внешней силы
Резонанс – явление резкого возрастания амплитуды вынужденных колебаний при определённом значении частоты вынуждающей силы. Резонансная частота – частота вынуждающей силы, при которой наступает резонанс.
31. Упругие волны. Волновое движение и его характеристики. Гармонические волны. Уравнение плоской гармонической волны. Виды волн. Скорость распространения упругих волн.
Процесс распространения колебаний частиц в упругой среде называется волновым процессом или просто волной. Часто эту волну называют упругой , т.к. она обусловлена упругими свойствами среды.
Упру́гие во́лны — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил. При распространении таких волн в среде перемещаются малые упругие колебания.
Волновое движение— это повторяющееся колебания частиц среды взад и вперед или из стороны в сторону. Он связан с переносом энергии в пространстве. Примеры волнового движения — звук, рябь на поверхности водоема, радиосигналы и свет.
У волны появляются новые характеристики:
Кроме повторения во времени, движение в волне повторяется и в пространстве.
Расстояние между точками среды, совершающими синфазные колебания, называется длиной волны λ. Скорость, с которой колебания распространяются в пространстве, называют скоростью распространения волны. Обозначается чаще буквой c. Очевидно, что длина волны, скорость и период колебаний частиц среды в волне связаны. λ = c · T. Плотностью потока энергии (или интенсивностью) I называют количество энергии, переносимой волной сквозь единицу площади за единицу времени.
Гармоническая волна — волна, при которой каждая точка колеблющейся среды или поле в каждой точке пространства совершает гармонические колебания (колебания, при которых физическая величина изменяется с течением времени по гармоническому (синусоидальному, косинусоидальному) закону).
Виды волн:
продольные – частицы среды совершают колебания по направлению распространения волны – во всех упругих средах.
поперечные – частицы среды совершают колебания перпендикулярно направлению распространения волны – на поверхности жидкости.
Виды механических волн:
упругие волны – распространение упругих деформаций;
волны на поверхности жидкости.
Характеристики волн:
-Скорость- расстояние, которое проходит волна за единицу времени (1 сек.). В однородной среде скорость постоянна. Скорость зависит от свойств среды – упругости и плотности (чем больше плотность и упругость среды, тем больше скорость волны). Скорость в твёрдых телах выше скорости в жидких средах, а в жидких средах – выше, чем в газах. Скорость волны – отношение длины волны к периоду.
- Длина волны- расстояние, которое прошла волна за время, равное периоду колебаний – расстояние между 2 точками, фазы которых в один и тот же момент времени отличаются на 2π. Единица измерения длины волны – метры.
- Фронт волны– геометрическое место точек, колеблющихся в одинаковой фазе.

Скорость распространения упругих волн
Упру́гие во́лны (звуковые волны) — волны, распространяющиеся в жидких, твёрдых и газообразных средах за счёт действия упругих сил.
В зависимости от частоты различают инфразвуковые, звуковые и ультразвуковые упругие волны.В жидких и газообразных средах может распространяться только один тип упругих волн — продольные волны. В волне этого типа движение частиц осуществляется в направлении распространения волны.В твёрдых телах существуют касательные напряжения, что приводит к существованию других типов волн, в которых движение частиц осуществляется по более сложным траекториям.Упругие волны, распространяющиеся в земной коре, называют сейсмическими волнами.
Скорость волны определяется скоростью распространения колебаний от одной точки среды к другой:так как то,.
Скорость распространения волн тем меньше, чем инертнее среда, т.е. чем больше ее плотность. С другой стороны, она имеет большее значение в более упругой среде, чем в менее упругой. Скорость продольных волн определяется по формуле:
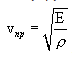 , а поперечной :
, а поперечной : 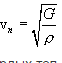 где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.
где ρ- плотность среды, E - модуль Юнга, G - модуль сдвига. Так как для большинства твердых тел E>G то скорость продольных волн больше скорости поперечных.Для идеально упругих сред, к которым относится большинство м-лов и т.п., установлена связь V с плотностью о и др.упругими параметрами — модулем Юнга Е и Пуассона коэф.ц
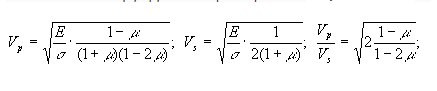
32. Энергетические характеристики упругих волн.
Полная механическая энергия упругой волны равна сумме потенциальной энергии и кинетической энергии:
Потенциальная энергия гармонической упругой плоской волны, распространяющейся вдоль оси 0x, равна:
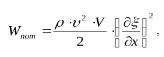
Кинетическая энергия равна :
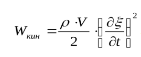
Чтобы учесть направление распространения энергии волны, существует характеристика, называемая плотностью потока энергии. Плотность потока энергии – это векторная физическая величина, модуль которой равен отношению потока энергии к площади поперечной поверхности, через которую она переносится, к значению этой площади, а направление совпадает с направлением скорости волны (т. е. вдоль луча)
33. Отражение волн. Принцип суперпозиции. Стоячие волны. Уравнение стоячей волны.
Отражение волн- переизлучение волн препятствиями с изменением направления их распространения (вплоть до смены на противоположное). Отражающими объектами могут быть непрозрачные тела, в к-рых волны данной природы распространяться не могут, неоднородности среды (как резкие, так и плавные). Обычно на границе раздела сред одновременно с О. в. происходит преломление волн. При падении плоской монохроматич. волны на плоскую границу раздела двух однородных сред с разными св-вами происходит зеркальное О. в. Амплитуды, фазы и направления распространения отражённой и преломлённой (прошедшей) волн определяются на основе согласования волн. полей по разные стороны от границы в соответствии с граничными условиями.
Принцип суперпозиции волн, установленный из опыта, состоит в том, что волны от разных источников, накладываясь друг на друга, не изменяются. Другими словами, распространение волны в данной среде не зависит от наличия в этой среде других волн.
Стоячая волна - это волна, которая образуется при наложении двух волн с одинаковой амплитудой и частотой, когда волны движутся навстречу друг другу.
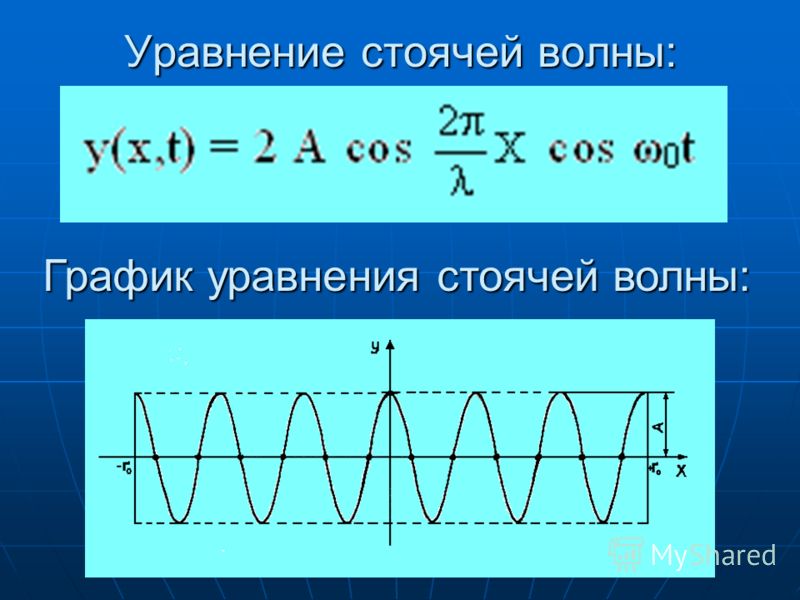
34. Интерференция волн. Принцип Гюйгенса и его применение для объяснения отражения, преломления и дифракции волн.
Интерференция -это перераспределение потока электромагнитной энергии в пространстве, возникающее в результате наложения волн, приходящих в данную область пространства от разных источников. Если в области интерференции световых волн поставить экран, то на нем будут наблюдаться светлые и темные области, например полосы.
Интерферировать могут толькокогерентные волны.Источники(волны) называют когерентными, если они имеют одинаковую частотуи постоянную во времени разность фаз, излучаемых ими волн.
Когерентными могут быть только точечные монохроматические источники. К ним по свойствам близки лазеры. Обычные источники излучения некогерентны, так как немонохроматичны и не являются точечными.
Немонохроматичность излучения обычных источников обусловлена тем, что их излучение создается атомами, испускающими в течение времени порядка =10-8 с волновые цуги длиной L=c =3м. Излучения разных атомов не коррелированы друг с другом.
Однако наблюдать интерференцию волн можно и при использовании обычных источников, если с помощью какого-либо приема создать два или более источников, подобных первичному источнику. Существует два метода получения когерентных световых пучков или волн: метод деления волнового фронтаиметод деления амплитуды волны. В методе деления волнового фронта пучок или волна делится, проходя через близко расположенные щели или отверстия (дифракционная решетка), либо с помощью отражающих и преломляющих препятствий (бизеркало и бипризма Френеля, отражательная дифракционная решетка)
Принцип Гюйгенса : каждая точка фронта (поверхности, достигнутой волной) является вторичным (т.е. новым) источником сферических волн. Огибающая фронтов волн всех вторичных источников становится фронтом волны в следующий момент времени.
Принцип Гюйгенса объясняет распространение волн, согласующееся с законами геометрической оптики, но не может объяснить явлений дифракции.
Для отражения и преломления: Таким образом, отношение синуса угла падения к синусу угла преломления равно отношению скорости волны в первой среде к скорости волны во второй среде.
Для дифракции волн: Явление дифракции состоит в том, что волны огибают встречаемые на пути препятствия, если размеры последних соизмеримы с длиной волны. Отклонение от прямолинейности наблюдается и при прохождении волн через малые отверстия, размеры которых сравнимы с длиной волны: волна заходит в область тени. Согласно принципу Гюйгенса каждая точка открытой части фронта волны (рис. 3), являясь самостоятельным источником, излучает волны по всем направлениям, в том числе и в область тени.
Вопрос 35
Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.
Диапазон звуковых частот лежит в пределах приблизительно от 20 Гц до 20 кГц. Волны с частотой менее 20 Гц называются инфразвуком, а с частотой более 20 кГц –ультразвуком.
Объективные характеристики звуковой волны:
Интенсивность волны - величина, равная потоку энергии, переносимой волной через единичную площадку, перпендикулярную направлению распространения волны:

Где Ф-поток звуковой энергии (Ф=W/t)W-звуковая энергия.
Частотой волны называется частота колебаний точек среды, в которой распространяется волна.
Спектральный состав (спектр) звука указывает, из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.
Если
Субъективные характеристики звуковой волны:
Громкость звука — субъективное восприятие силы звука (абсолютная величина слухового ощущения). Громкость главным образом зависит от амплитуды
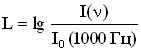 Уровень громкости равен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при частоте 1000 Гц на пороге слышимости:
Уровень громкости равен десятичному логарифму отношения интенсивности звука при данной частоте к интенсивности звука при частоте 1000 Гц на пороге слышимости:Субъективную меру частоты колебаний звука называют высотой звука. Звуковые колебания, происходящие по гармоническому закону, воспринимаются человеком как определенный музыкальный тон. Колебания высокой частоты воспринимаются как звуки высокого тона, звуки низкой частоты – как звуки низкого тона.
Темб ром на зы ва ет ся окрас ка звука(это то, чем от ли ча ют ся два оди на ко вых звука, ис пол нен ные раз лич ны ми му зы каль ны ми ин стру мен та ми.)
Вопрос 36
Скорость звука — скорость распространения звуковых волн в среде.
Где β — адиабатическая сжимаемость среды;ρ — плотность
Эффект Доплера
Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны) зависит от скорости и направлениядвижения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется — длина волны увеличивается.
Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сиренавыдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тоттон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится (а длинауменьшится), и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будетпроезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше ибудет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты (и, соответственно, большей длины) звуковых волн.
Излучение звука - возбуждение звуковых волн в упругой среде (воздухе, воде), окружающей источник звука. Звуковое поле, создаваемое данным излучателем, существенно зависит от формы излучателя и вида его колебаний, а также от частоты, определяющей соотношение между размерами излучателя и длиной волны l излучаемого им звука
Распространение звука:
Звук распространяется в любой упругой среде -твердой, жидкой и газообразной, но не может распространяться в пространстве, где нет вещества (например, в вакууме)
Вопрос 37
Свойства жидкостей:
1)Сжимаемость – это способность жидкости изменять свой объём при изменении давления.
Сжимаемость жидкости характеризуется коэффициентом объёмного сжатия
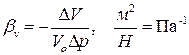
∆V – изменение объема жидкости под воздействием изменения давления, м3.
Vo – первоначальный объем жидкости, м3;
∆p – изменение давления в жидкости
2) Температурное расширение – это свойство жидкости изменять объём при изменении температуры. Это свойство жидкости характеризуется коэффициентом температурного расширения, который показывает относительное увеличение
( или уменьшение ) объёма жидкости из-за изменения ее температуры
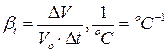 .
. 3) Вязкость – свойство жидкости, которое определяет сопротивление жидкости к внешнему воздействию. Вязкость можно представить как внутреннее трение между отдельными слоями жидкости при их смещении относительно друг друга.
Закон Ньютона-Петрова:
где - сила внутреннего трения слоев жидкости,
- площадь соприкасающихся слоев,
- динамический коэффициент вязкости,
- разность скоростей двух соседних слоев жидкости, расположенных на расстоянии друг от друга по нормали
формула Пуазейля:
Q- Поток жидкости, R-радиус круглого сечения, р- разности давлений на концах трубки, l-длинна трубы , -коэффициент вязкости
Выразим из неё коэффициент вязкости:
Свойства газов:
Газ всегда заполняет объём, ограниченный непроницаемыми для него стенками
Стремясь расшириться, газ оказывает давление
Молекулы газа ударяют о стенки сосудов, а затем отлетают со скоростью, почти, что равной скорости молекулы до удара. При ударе молекула передает стенке количество движения.
Механическое равновесие означает, что не происходит движения отдельных частей газа. Для этого необходимо, чтобы давление газа было во всех его частях одинаково
Тепловое равновесие означает, что не происходит передачи теплоты от одного участка газа к другому. Для этого необходимо, чтобы температура во всем объеме газа была одинакова.
Гидростатика
Гидростатика – теория равновесия жидкостей и газов относительно выбранной системы координат.
Состояние покоя жидкости определяется равенством всех сил, действующих на ее частицы. Это условие может быть реализовано как в неподвижной системе координат (связанной с землей), так и в подвижной системе отсчета (например, закрепленной на стенках подвижных резервуаров).
Равновесное состояние жидкости, находящейся в покое относительно неподвижной системы координат, называется абсолютным покоем, а в подвижной – относительным покоем.
Закон Паскаля
Давление в любом месте покоящейся жидкости одинаково по всем направлениям, причем давление одинаково передается по всему объему, занятому данной жидкостью.
Для несжимаемой жидкости на глубине h действует гидростатическое давление
т.е. давление изменяется линейно с высотой. Давлениеghназывается гидростатическим.
Закон Архимеда
На тело, погруженное в жидкость (газ), действует со стороны этой жидкости (газа) направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости (газа).

39. Импульс жидкостей и газов. Реакция струи.
Распространение импульса обусловлено наличием упругих сил, возникающих в жидкости или газе. Но жидкости и газы обла дают упругостью только в отношении изменения объёма и не обла дают упругостью в отношении сдвига. Поэтому, в отличие от твёрдых тел, в жидкостях и газах могут распространяться только импульсы сжа тия и разрежения, т. е. продольные импульсы. Импульс всегда будет распространяться либо в направлении, в котором начали двигаться частицы жидкости или газа в месте возникно вения импульса (импульс сжатия), либо в про тивоположном направлении (импульс разре жения).
Скорость распространения продольного импульса в жидкости или газе можно рассчитать совершенно так же, как и скорость продольного импульса в твёрдом теле. Пусть импульс сжатия соответствует увеличению плотности на Др и увеличению давления на Др. Через площадку S, перпендикулярную к направлению распространения импульса, за время N проходит «часть импульса» с At, где с — скорость распространения импульса. Прохождение этого участка импульса связано с увеличением массы справа от площади 5 на величину Am = Др S'cAt. При этом через площадку передаётся количество движения
Am-c = ApSc2At.
Скорость импульса определяется только тем, как изменяется плотность среды при изменении давления. Скорость импульса не зависит от его формы и амплитуды. Поэтому всякие быстропеременные давления в жидкости или газе, и, в частности, звуки распространяются в среде в большинстве случаев с той же скоростью, с какой распространяются отдельные импульсы.
Реакцией струи называется сила, возникающая при истечении жидкости из насадка. Эта сила обуславливается изменением количества движения жидкости в насадке при движении от большего сечения к меньшему.
Пусть количество движения секундной массы жидкости в большем сечении насадка , а в меньшем .
Для определения величины и направления силы F воспользуемся законом изменения количества движения, согласно которому
Учитывая, что значительно меньше и членом можно пренебречь, получим:
Подразумевая под секундной массой массу жидкости, соответствующую расходу Q, т.е. , и выражая расход через скорость
Умножая числитель и знаменатель дроби на 2g, после подстановки
Знак минус указывает, что сила реакции направлена в сторону, противоположную движению струи.
Сила реакции струи для ручных стволов при напоре до 50 м достигает 500 H; для лафетных стволов, работающих и при больших напорах, сила реакции увеличивается в несколько раз.
40. Силы внутреннего трения (вязкости). Течение вязкой жидкости по цилиндрической трубе. Формула Пуазейля. Ламинарное и турбулентное течение.
Вязкость— это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой. При перемещении одних слоев реальной жидкостиотносительно других возникают силывнутреннего трения, направленные по касательнойк поверхности слоев.
В соответствии с третьим законом Ньютона силы внутреннего трения равны по величине и противоположны по направлению, поэтому верхний слой замедляет движение нижнего, а нижний - ускоряет движение верхнего (см. рис. 13.1). Величина силы внутреннего трения задается формулой Ньютона:
Fтр = η·|Δ/Δz|·S, или
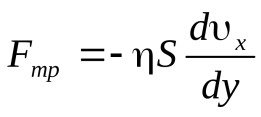 (13.2)
(13.2)где η - коэффициент вязкости;
|Δ/Δz| - модуль градиента скорости, показывающий, как быстро меняется величина вектора скорости в направлении, перпендикулярном течению жидкости. Градиент скорости ∆v/∆x показывает, как быстро меняется скорость при переходе от слоя к слою в направлении xперпендикулярном направлению движения слоев.
S - площадь поверхности соприкасающихся слоев жидкости.
Коэффициент пропорциональности η, зависящий от природы жидкости и температуры, называется динамической вязкостью(или просто вязкостью). Физический смысл коэффициента вязкости вытекает из выражения (13.2):
коэффициент вязкости численно равен силе внутреннего трения, действующей на единицу площади поверхности соприкасающихся слоев, при единичном градиенте скорости.
В системе СИ вязкость измеряется в Па·с, а в СГС - в пуазах (Пз): 1 Па·с = 10 Пз. Коэффициент вязкости жидкости зависит от природы жидкости (в частности, ее плотности) и температуры, уменьшаясь с ростом последней по экспоненциальному закону. Для более объективного учета характера взаимодействия молекул в непрерывных средах с разной плотностью, например, в жидкостях и газах, вводят понятие кинематического коэффициента вязкости.
Жидкость, протекающую по цилиндрической трубе радиуса R, можно представить разделенной на концентрические слои (рис.10). В каждом таком слое скорость течения постоянна, но от слоя к слою изменяется. Слой, прилипший к стенкам трубы, имеет скорость, равную нулю, Vmin=0. Слой, текущий вдоль оси трубы, имеет максимальную скорость Vmax. Профиль скорости в этом случае является параболой (рис.10, а). Вдоль радиуса трубы (ось r) скорость изменяется, и это изменение характеризуется величиной .
Задача о течении вязкой жидкости по цилиндрическим трубам имеет исключительно важное значение для физиологии, так как кровеносная система является системой из многократно разветвляющихся цилиндрических сосудов различных диаметров.
Важнейшую закономерность течения вязкой жидкости по цилиндрическим трубам представляет формула Пуазейля, позволяющая рассчитать объем жидкости, протекающий через поперечное сечение трубы за одну секунду:
,
где - объем жидкости, протекающей через поперечное сечение трубы за время . Используя формулу (1), можно записать
,
где
Ламинарное течение. Отличие ламинарного течения от турбулентного состоит в характере и направлении водных (газовых) потоков. Они перемещаются слоями, не смешиваясь и без пульсаций. Другими словами, движение проходит равномерно, без беспорядочных скачков давления, направления и скорости. Ламинарное течение жидкости образуется, например, в узких кровеносных сосудах живых существ, капиллярах растений и в сопоставимых условиях, при течении очень вязких жидкостей (мазута по трубопроводу). Чтобы наглядно увидеть струйный поток, достаточно немного приоткрыть водопроводный кран – вода будет течь спокойно, равномерно, не смешиваясь. Если краник отвернуть до конца, давление в системе повысится и течение приобретет хаотичный характер.
Турбулентное течение. В отличие от ламинарного, в котором близлежащие частицы движутся по практически параллельным траекториям, турбулентное течение жидкости носит неупорядоченный характер. Если использовать подход Лагранжа, то траектории частиц могут произвольно пересекаться и вести себя достаточно непредсказуемо. Движения жидкостей и газов в этих условиях всегда нестационарные, причем параметры этих нестационарностей могут иметь весьма широкий диапазон. Как ламинарный режим течения газа переходит в турбулентный, можно отследить на примере струйки дыма горящей сигареты в неподвижном воздухе. Вначале частицы движутся практически параллельно по неизменяемым во времени траекториям. Дым кажется неподвижным. Потом в каком-то месте вдруг возникают крупные вихри, которые движутся совершенно хаотически. Эти вихри распадаются на более мелкие, те – на еще более мелкие и так далее. В конце концов, дым практически смешивается с окружающим воздухом.
41. Движение тел в жидкостях и газах.
На тело, движущееся в жидкости или газе, действуют две силы (равнодействующую их обозначим ), одна из которых (Rx) направлена в сторону, противоположную движению тела (в сторону потока),—лобовое сопротивление, а вторая (Ry) перпендикулярна этому направлению—подъемная сила.
Если тело симметрично и его ось симметрии совпадает с направлением скорости, то на него действует только лобовое сопротивление, подъемная же сила в этом случае равна нулю. Можно доказать, что в идеальной жидкости равномерное движение происходит без лобового сопротивления. Если рассмотреть движение цилиндра в такой жидкости (рис.56), то картина линий тока симметрична как относительно прямой, проходящей через точки А и В,так и относительно прямой, проходящей через точки Си D, т. е. результирующая сила давления на поверхность цилиндра будет равна нулю.
Иначе обстоит дело при движении тел в вязкой жидкости (особенно при увеличении скорости обтекания). Вследствие вязкости среды в области, прилегающей к поверхности тела, образуется пограничный слой частиц, движущихся с меньшими скоростями. В результате тормозящего действия этого слоя возникает вращение частиц и движение жидкости в пограничном слое становится вихревым. Если тело не имеет обтекаемой формы (нет плавно утончающейся хвостовой части), то пограничный слой жидкости отрывается от поверхности тела. За телом возникает течение жидкости (газа), направленное противоположно набегающему потоку. Оторвавшийся пограничный слой, следуя за этим течением, образует вихри, вращающиеся в противоположные стороны (рис. 57).
Лобовое сопротивление зависит от формы тела и его положения относительно потока, что учитывается безразмерным коэффициентом сопротивления Сx, определяемым экспериментально:
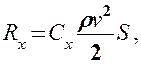 (33.1)
(33.1)где — плотность среды; — скорость движения тела; 5 — наибольшее поперечное сечение тела.
Составляющую Rx можно значительно уменьшить, подобрав тело такой формы, которая не способствует образованию завихрения.
Подъемная сила может быть определена формулой, аналогичной (33.1):
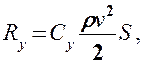
где Су— безразмерный коэффициент подъемной силы.
42. Волны на поверхности воды.
Продольные и поперечные волны
Продольные волны
ОПРЕДЕЛЕНИЕ
Продольная волна – это волна, при распространении которой смещение частиц среды происходит в направлении распространения волны (рис.1, а).
Причиной возникновения продольной волны является деформация сжатия/растяжения, т.е. сопротивление среды изменению ее объема. В жидкостях или газах такая деформация сопровождается разрежением или уплотнением частиц среды. Продольные волны могут распространяться в любых средах – твердых, жидких и газообразных.
Примерами продольных волн являются волны в упругом стержне или звуковые волны в газах.
Поперечные волны
ОПРЕДЕЛЕНИЕ
Поперечная волна – это волна, при распространении которой смещение частиц среды происходит в направлении, перпендикулярном распространению волны (рис.1,б).
Причиной поперечной волны является деформация сдвига одного слоя среды относительно другого. При распространении поперечной волны в среде образуются гребни и впадины. Жидкости и газы, в отличие от твердых тел, не обладают упругостью по отношению к сдвигу слоев, т.е. не оказывают сопротивления изменению формы. Поэтому поперечные волны могут распространяться только в твердых телах.
Примерами поперечных волн могут служить волны, бегущие по натянутой веревке или по струне.
Волны на поверхности жидкости не являются ни продольными, ни поперечными. Если бросить на поверхность воды поплавок, то можно увидеть, что он движется, покачиваясь на волнах, по круговой траектории. Таким образом, волна на поверхности жидкости имеет как поперечную, так и продольную компоненты. На поверхности жидкости также могут возникать волны особого типа – так называемые поверхностные волны. Они возникают в результате действия силы тяжести и силы поверхностного натяжения.

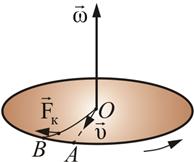 на шарик движущийся с постоянной скоростью относительно вращающейся системы отсчета ,действует сила перпендикулярная к скорости .В результате действия этой силы (Кариолиса)скорость шарика не меняет свое направление.
на шарик движущийся с постоянной скоростью относительно вращающейся системы отсчета ,действует сила перпендикулярная к скорости .В результате действия этой силы (Кариолиса)скорость шарика не меняет свое направление.
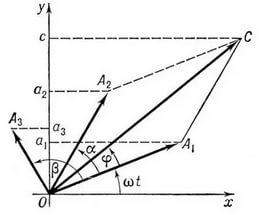
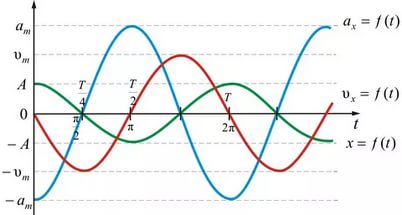
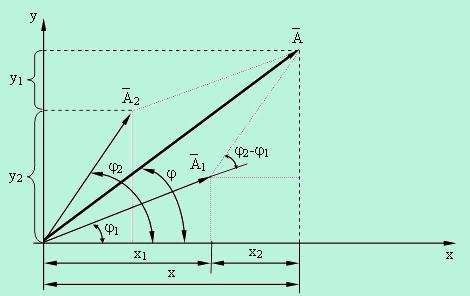
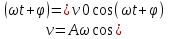 ,v0=A - амплитуда скорости;
,v0=A - амплитуда скорости; 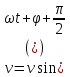 , следовательно скорость опережает по фаза смещения на четверть периода.
, следовательно скорость опережает по фаза смещения на четверть периода.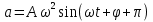 ,
,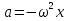 .
.