Отсчета. Способы описания движения. Кинематические характеристики движения точки. Траектория. Путь. Перемещение. Скорость. Мгновенная и средняя скорость. Ускорение

• Название: Отсчета. Способы описания движения. Кинематические характеристики движения точки. Траектория. Путь. Перемещение. Скорость. Мгновенная и средняя скорость. Ускорение
• Дата: 20.06.2018
• Размер: 1.75 Mb.
• Имя файла: Mekhanika.docx
• Тип: Документы; #47410
• страница: 3 из 4

Абсолютно упругий удар протекает в два этапа. Первый этап – От начала соприкосновения шаров до выравнивания скоростей – протекает также, как и при абсолютно неупругом ударе, с той лишь разницей, что силы взаимодействия ( как силы упругости) зависят только от величины деформации и не зависят от скорости её изменения. Пока скорости шаров не сравнялись деформация будет нарастать и силы взаимодействия, замедляющие один шар и ускоряющие другой. В момент, когда скорости шаров сравняются, силы взаимодействия будут наибольшими, с этого момента начинается второй этап упругого удара: деформированные тела действуют друг на друга в том же направлении, в каком они действовали до выравнивания скоростей. Поэтому то тело, которое замедлялось будет продолжать замедляться, а то которое ускорялось – ускоряться, до тех пор пока деформация не исчезнет. При восстановлении формы тел вся потенциальная энергия вновь переходит в кинетическую энергию шаров, т. о. при абсолютно упругом ударе тела не изменяют своей внутренней энергии.

Будем считать, что два соударяющихся шара образуют замкнутую систему, в которой силы являются консервативными. В таком случаи работа этих сил приводит к увеличению потенциальной энергии взаимодействующих тел. Закон сохранения энергии запишется следующим образом:



где  - кинетические энергии шаров в произвольный момент времени t (в процессе удара), а U - потенциальная энергия системы в тот же момент.  − значение тех же величин в другой момент времени t′. Если момент времени t соответствует началу соударения, то  ; если t′ соответствует концу соударения, то  Запишем законы сохранения энергии и импульса для двух этих моментов времени:

 (8)

 (9)

Решим систему уравнений (9) и (10) относительно 1 v′ и 2 v′. Для этого перепишем её в следующем виде:

 (10)



Поделим первое уравнение на второе:

 (11)

Решая систему из уравнения (11) и второго уравнения (10), получим:

 ,  (12)

Здесь скорости имеют положительный знак, если они совпадают с положительным направлением оси, и отрицательный – в противном случаи.

Переход механической энергии во внутреннюю.

При ударах механическая энергия переходит во внутреннюю.

14.Поступательное и вращательное движение твёрдого тела. Угловое перемещение, угловая скорость, угловое ускорение. Аксиальные вектора. Правило буравчика для определения угловой скорости.

Поступательное движение наз такое движение, при котором каждая линия, соединяющая 2 любые точки тела, сохраняет параллельность самой себе. В большинстве случаев такое движение можно описать одной точкой движения ЦМ.

Вращательное движение, при котором траектория каждой точки тела является концентрическими окружностями, с центром на одной прямой наз осью вращения.

Угловое перемещение(φ) – угол, на котором поворачивается перпендикуляр, опущенный из произвольной точки тела на ось вращения за опред времени.

φ=const измеряется в радианах.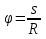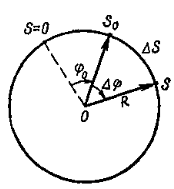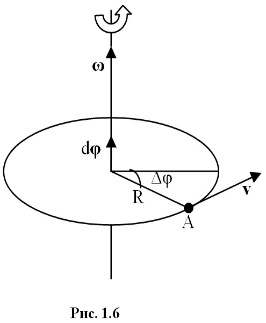

Угловой скоростью(ὦ) равномерного движения точки по окружности, т.е. в случае, когда модуль скорости не изменяются, наз физическую величину, пропорциональную углу поворота радиус-вектора, соединяющего центр окружности с движущей точкой, за единицу времени. 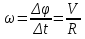Измеряется в рад/с.Направление скорости вдоль оси вращения определяется по правилу буравчику. При изменении направления вращения скорость изменяется напротив.

Угловое ускорение(β). Неравномерность движения можно также характеризовать угловой величиной. 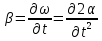(2я производная) . Направление, как и у скорости. Измеряется в рад/с^2.

Аксиальный вектор или псевдовектор — величина, компоненты которой преобразуются как вектор при поворотах системы координат, но меняющие свой знак противоположно тому, как ведут себя компоненты вектора при любой инверсии (обращении знака) координат. Т.е. псевдовектор меняет направление на противоположное при сохранении абсолютной величины (домножается на минус единицу) при любой инверсии координатной системы.

Правило буравчика:если вращать винт в том же направлении, в каком вращается тело, он завинтится в сторону направления угловой скорости.
15.Равномерное и равнопеременное вращение твёрдого тела. Графики зависимости угловых кинематических характеристик от времени для равномерного вращения и их анализ.

Равномерным – вращение, при котором угловая скорость тела остается во все время движения постоянной (ω = const). dφ = ωdt; φ = φ0 + ωt.

Равнопеременное - вращение, при котором угловое ускорение тела во все время движения остается постоянным (β = const).ω = ω₀ + βt φ = φ₀ + ω₀t + βt²/2

 Если величины ω и β имеют одинаковые знаки, вращение будет равноускоренным, а если разные - равнозамедленным.

ГРАФИКОВ НЕТ

16.Момент инерции твёрдого тела относительно неподвижной оси вращения. Расчёт момента инерции тел правильной геометрической формы (кольца, цилиндра, тонкого стержня, шара) относительно неподвижной оси, проходящей через центр масс. Теорема о параллельных осях (теорема Штейнера-Гюйгенса).

Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат кратчайшего расстояния от оси.

Вычисление момента инерции тела проводится по формуле

Вид твердого тела	Положение оси	Момент инерции
Тонкий стержень длины L	Перпендикулярно стержню
Сплошной цилиндр радиуса R	Совпадает с осью цилиндра
Тонкий диск радиуса R	Совпадает с диаметром диска
Шар радиуса R	Проходит через центр шара

теоремой Штейнера: момент инерции I относительно произвольной оси равен моменту инерции относительно оси параллельной данной и проходящей через центр масс С тела, плюс произведение массы т тела нa квадрат расстояния а между осями:

17.Основное уравнение динамики вращательного движения твёрдого тела и примеры его применения. Момент силы. Плечо силы. Момент инерции материальной точки. Аддитивность момента инерции.

Чтобы описать вращательное движение, связав причину движения (воздействующую силу) и следствие (приобретение углового ускорения), используют основное уравнение динамики вращательного движения: 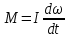Здесь M=Fr – момент силы, характеризующий, насколько интенсивно сила воздействует на тело. Произведение 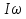 = L – это момент количества движения всех точек тела относительно оси вращения. Иногда его также называют «импульс вращения».

Вращение маятника Обербека происходит под действием момента М силы натяжения нити и противоположно направленного момента сил трения Мтр. Таким образом, согласно равенству уравнение движения маятника имеет вид:

Плечо силы  — это длина перпендикуляра, опущенного от оси вращения на линию действия силы. Момент силы — это физическая величина, равная произведению модуля силы на ее плечо: М= Fd

Правило аддитивности: сумма моментов инерции частей системы относительно оси равен мо Момент инерции — скалярнаяфизическая величина, мера инертности вовращательномдвижениивокруг оси, подобно тому, как масса тела является мерой его инертности впоступательном движении.

Момент инерциитвёрдого тела относительно какой-либо оси зависит не только отмассы, формы и размеров тела, но также от положения тела по отношению к этой оси. СогласнотеоремеШтейнера(теореме Гюйгенса-Штейнера),момент инерциителаJотносительно произвольной оси равен суммемоментаинерцииэтоготелаJcотносительно оси, проходящей черезцентрмасстела параллельно рассматриваемой оси, и произведениямассытелаmна квадрат расстоянияdмежду осями:



менту инерции системы относи-тельно данной оси.

18. Момент импульса материальной точки и твёрдого тела относительно неподвижной оси. Закон сохранения момента импульса.

Момент импульса(L)характеризует количество вращательного движения.Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса Lz не зависит от положения точки 0 на оси z. L=Iω

Закон сохранения момента импульса

Из основного закона уравнения динамики вращательного движения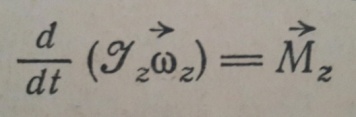следует ,что если на тело никакие внешние силы не действуют или действуют такие силы ,результирующий момент которых относительно оси z равен нулю ,то момент импульса тела относительно этой оси будет величиной постоянной:в этом и состоит закон сохранения момента импульса,вращающегося вокруг неподвижной оси.

19. Кинетическая энергия вращающегося тела. Работа, совершаемая при повороте тела на некоторый угол.

Кинетическая энергия вращающегося тела. Кинетическая энергия одного элемента Е_к =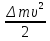.Кинетическая ее энергия (Т)всего тела слагается из энергий отдельных его элементов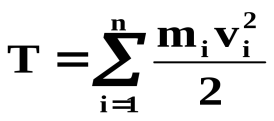

Пусть тело вращается относительно оси z тогда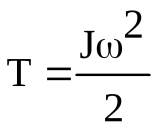.По определению величины=I_z (момент инерции).Поэтому .Кинетическая энергия вращающегося тела равна половине произведения момента инерции тела относительно оси вращения на квадрат угловой скорости.

Работа ,совершаемая при повороте на некоторый угол  Если м.т. вращается по окружности, то на нее действует сила  , то при повороте на некоторый угол совершается элементарная работа: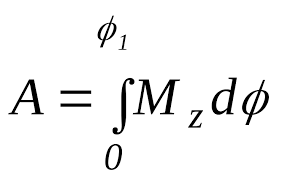

 ,

 



20. Условия равновесия твёрдого тела. Решение задач статики.

Тело находится в положении равновесия ,когда ее скорость и сумма действующих сил равны нулю.

Если сумма сил(сила) ,возникающая при отклонении тела(точки) от положения равновесия ,такова, что она что возвращает тело в положение равновесия ,то такое равновесие называют устойчивым.(сохраняется сколько угодно). Потенциальная энергия минимальна.

Если сила, появляющаяся при отклонении, будет и дальше удалять тело от положения равновесия ,то это неустойчивое равновесие. Потенциальная энергия максимальна.Тело не может длительно прибывать в этом положении.

Если при смещении тела из положения равновесия силы не возникают,равновесие называют безразличным.

Пример.Найдем положение устойчивого равновесия груза, подвешенного на пружине. Потенциальная энергия состоит из двух слагаемых :энергии Uупр=,обусловленной упругой деформацией пружины и энергией Uграв=-mgx(ось х направлена вниз),обусловленной гравитационным взаимодействием. Полная энергия системы равна U=Uупр+Uграв

U=-mgx.Приравнивая производную к нулю 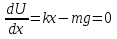получаем уравнение,из которого находим координату положения устойчивого равновесия:x=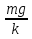

21. Понятие неинерциальной системы отсчёта (НИСО). Виды НИСО. Поступательно движущиеся и вращающиеся НИСО. Сила инерции в поступательно движущейся НИСО. Центробежная сила инерции. Сила Кориолиса.НИСО.

Неинерциальными называют такие системы отсчета, в которых не выполняются законы Ньютона.НИСО движутся с ускорением относительно какой-либо инерциальной системы.

Различают два вида НИСО:

1)системы ,движущиеся относительно инерциальной системы отсчета поступательно с потоянным или переменным ускорением.

Пример.На горизонтальном прямолинейном участке железнодорожного пути находится вагон.На полу вагона лежит неподвижный шар,могущий перемещаться на полу без силы трения.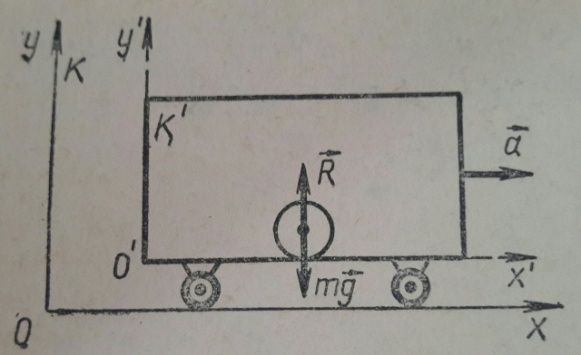

Две системы отсчета:(К)свяжем с поверхностью земли(инерциальная),(K')-со станками вагона.(инерциальная только тогда, когда вагон покоится или движется равномерно и прямолинейно).

Вагон покоится -шар не подвижен в обоих системах.

Вагон движется с ускорением. Наблюдатель в системе К’(неинерциальная система отсчета ,движущаяся поступательно) скажет ,что шар движется с ускорением(по модулю равно ускорению вагона),так же отметит ,что ускорение тела не зависит от массы этого тела(без силы трения);оно одинаково для всех тел и равно ускорению,с которым движется система К’, взятому с обратным знаком(а=-а)это справедливо когда сумма ньютоновских сил равна 0.