ВОПРОСЫ и ответы К ЭКЗАМЕНУ. Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины
 Скачать 2.8 Mb.
|
|
14. Полнота в логике высказываний. Штрих Шеффера и стрелка Пирса. В исчислении высказываний, кроме явных определений, существуют неявные. К ним относится стрелка Пирса,АВ .Это сложное высказывание, которое означает "НиА, ниВ".Например, " новое здание было ни высоким (А), ни низким(В)". Это высказывание истинно только тогда, когда ложны оба высказывания, входящие в это сложное высказывание. Таблица истинности сложного высказывания видаАВ выглядит следующим образом: 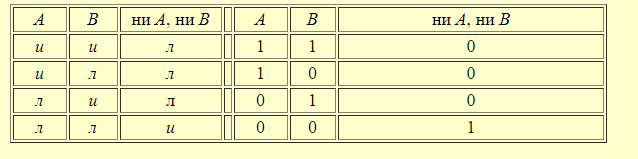 Для сравнения приведём таблицу истинности для дизъюнкции А В, в котором союз "или" употреблён в соединительно -разделительном смысле. 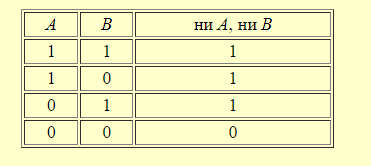 Одно из направлений современной неклассической математической логики, в котором не применяется операция отрицания называется "положительная логика". Одной из таких логических построений является логика, построенная с помощью одного функтора логического знака операции) "/" , который называется "штрих Шеффера". Например,А/Возначает: "АиВнесовместны" или "Неверно, чтоА и В". Ещё пример, высказывания "2 х 2 = 4" и "2 х 2 = 5" несовместны. Высказывание со штрихом Шеффера истинно тогда и только тогда, когда либоАложно, либоВложно , либоА и Вложны одновременно. Оно ложно и в ом случае, если истинны иАи Водновременно. Действительно, если вместо А подставить высказывание "2 х 2 = 4" и вместо В подставить высказывание "2 х 2 = 4", тоА/Вдадут ложное высказывание, так как так про идентичные высказывания нельзя сказать, что они несовместны. Таблица истинности со штрихом Шеффера выглядит следующим образом 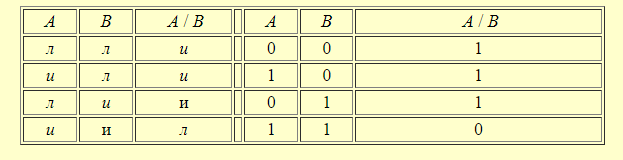 Как видно из таблицы, операция со знаком "/" является противоположной операции операции со знаком "". Операция истинностного значения сложного высказывания А В выглядит так: 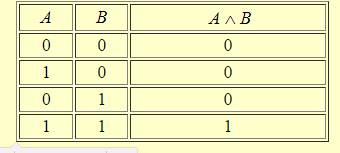 На этом основании всегда можно вывести формулу:А/В≡  , которая читается так: "НесовместностьА и Вравносильна отрицанию конъюнкцииА и В"Сложное высказывание можно выразить и через дизъюнкцию, которая примет следующий вид: А/В ≡  То есть, "несовместность А и В равносильна дизъюнкции отрицаний"С помощью штриха Шиффера можно выразить все другие связки исчисления высказываний, что и сделал сам Шиффер. построив всю теорию исчислений высказываний с помощью только одного знака операции. В этой системе действительны следующие равнозначности: Ā ≡ А / А"ОтрицаниеАравносильно тому, чтоА и Анесовместны" АВ≡  " А и Вравносильно операции несовместности"АВ ≡  "А или Вравносильно тому. что отрицание А и отрицание Внесовместны"АВ ≡  "ЕслиА имплицирует (влечёт) В.то это равносильно тому. что, чтоА и отрицание Внесовместны".Операция штрих Шеффера коммутативна: А / В≡ В /А Но операция не подчиняется закону ассоциативности: А / (В / С) ≠ (А / В) / С Полнота логических исчислений — выводимость в исчислении (логической системе) всех утверждений (предложений, формуЛит.п.), обладающих некоторым подразумеваемым для этого исчисления свойством. Напр., П. классического исчисления высказываний (в какой-нибудь из возможных формулировок) означает выводимость в нем всех тождественно истинных формул логики высказываний. 15. Понятие множества. Подмножества. Равенство множеств. Универсум. Пустое множество. Операции над множествами. Мы будем понимать под множеством всякую совокупность каких-либо объектов. Объекты этой совокупности есть элементы данного множества. Обычно множества обозначаются прописными, а элементы множества строчными буквами. Принадлежность элементамножествуобозначается  ( принадлежит).Если элементне принадлежит множеству,то, в этом случае, используется обозначение  .Множество называется подмножеством множества , если всякий элемент множества является элементом множества . При этом используется обозначение  . Знак называется знаком включения. В этом случае говорят, что В содержит А.Способы задания множеств Обычно выделяют следующие способы задания множеств:спискомсвоих элементов;порождающей процедуройилиописаниемхарактеристических свойств, которыми должны обладать его элементы. Списком можно задавать лишь конечные множества. Список обычно заключают в фигурные скобки, например,  означает, что множествосостоит из четырех элементов  .Порождающая процедура описывает способ получения элементов множества из уже полученных элементов либо из других объектов. Элементами множества считаются все объекты, которые могут быть построены с помощью такой процедуры. Операции над множествами ОбъединениеммножествАиВназывается множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств.Объединение обозначается  . или  Объединение множеств, принадлежащих произвольной (в том числе бесконечной) системе множеств, определяется аналогично. При этом используются следующие обозначения:  – объединение множествА, В, С, D;Пусть  ,  , тогда  .Пересечением множествиВназывается множество, состоящее из тех и только тех элементов, которые принадлежат иАиВ. Обозначение  . и  .Аналогично, как для операции объединения определяется пересечение произвольной, в том числе и бесконечной системы множеств. Пример 5 Пусть  ,  , тогда  ;Дополнениеммножестваназывается множество всех элементов, не принадлежащих(но принадлежащих  )  Пример 7 Пусть  − множество точек плоскости, находящихся в круге радиуса 1, тогда  – внешность единичного круга.Дополнениеммножестваназывается множество всех элементов, не принадлежащих(но принадлежащих ) Пример 7 Пусть − множество точек плоскости, находящихся в круге радиуса 1, тогда – внешность единичного круга.Пустым множеством называют множество, не содержащее ни одного элемента. Универсальное множество U(илиуниверсум) есть множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами. В теории чисел универсальное множество обычно совпадает с множеством всех целых или натуральных чисел. В математическом анализе универсальное множество может быть множество всех действительных чисел или множество всех точекn-мерного пространства. Следует отметить, что универсальное множествоU, хотя, и названо универсальным, однозначно не определено, если точно не указана область рассмотрения (предметная область). Конечно, любое множество, содержащееU, может быть использовано как универсальное множество. По определению, каждое множество есть подмножество универсального множества Пример.. Так для множества  за универсум можно взять множество натуральных чисел, т.е. U=N.. Равенство множеств A = B это утверждение, которое означает, что множества состоят из одних и тех же элементов. Более подробно: любой элемент множества A принадлежит множе-ству B и любой элемент множества B принадлежит множеству A. Эти два условия естественно разделить. 16. Операции над множествами. Определение 1.5. Объединением множеств A и B называется множество, (которое обозначается AВ) состоящее из всех элементов, которые принадлежат хотя бы одному из множеств А или В. 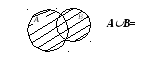 Пересечением множеств А и Вназывается множество, (которое обозначается АВ) которое состоит из общих элементов этих множеств. 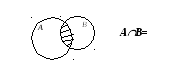 Определение 1.7. Разностью множеств А и В называется множество, (которое обозначается А\В) всех тех и только тех элементов множества А, которые не принадлежат В. Определение 1.8. Симметрическая разность множеств А и В (обозначается А∆В) есть множество (А\В)(В\А).  Определение 1.9. Дополнением множества А (обозначается ) – это множество элементов универсума, которые не принадлежат А, т.е. 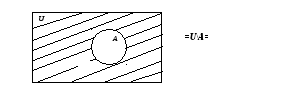 \А. 17. Основные свойства операций над множествами.  Теорема 1.Для произвольных множеств А ,В и С справедливы следующие свойства: 1. Коммутативность пересечения и объединения:  .  ;2. Ассоциативность пересечения и объединения:  ;  ;3. Дистрибутивность пересечения относительно объединения:  ;Дистрибутивность объединения относительно пересечения:  ;4. Идемпотентность пересечения и объединения:  , ;5.  =U;  =Ø6. Законы де Моргана:  =  ; =  7. Законы поглощения:  U; =Ø; U=U;  ; Ø=A;  Ø= Ø;8.  ; 9. Закон инволюции:= 10. Закон исключения разности:  . |