ВОПРОСЫ и ответы К ЭКЗАМЕНУ. Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины
 Скачать 2.8 Mb.
|
|
| | |
Свойство бинарных отношений:
1) Рефлексивность. Пусть на множестве А задано бинарное отношение R. Бинарное отношение называется рефлексивным, если для любого элемента А упорядоченная пара из этого элемента принадлежит R: для любого A(a,a) Î R. Т.е. бинарное отношениена множественазываетсярефлексивным, если всякий элемент этого множества находится в отношениис самим собой.
Матрица рефлексивного отношения на диагонали содержит 1, а граф бинарного отношения имеет петли.
2)Антирефлексивность. Бинарные отношения являются антирефлексивными, если: для любого A(a,a) Ï R.
Матрица антирефлексивного отношения на диагонали содержит 0, а граф не имеет петель.
3)Симметричность.Бинарное отношениена множестве X называетсясимметричным, если для каждой пары элементов множествавыполнение отношениявлечёт выполнение отношения. Отношениесимметрично, если
.Матрица симметричного бинарного отношения симметрична относительно главной диагонали. В графе все пары вершин соединены 2-мя противоположно направленными дугами.
4)Антисимметричночть. В математике бинарное отношениена множестве X называетсяантисимметричным, если для каждой пары элементов множествавыполнение отношенийивлечёт, или, что то же самое, выполнение отношенийивозможно только для равныхи.
| | |
Матрица антисимметричного бинарного отношения не симметрична относительно главной диагонали, в графе отсутствуют противоположно направленные дуги.
5)Транзитивность.Бинарное отношение называют транзитивным, если:
В графе задающего транзитивное бинарное отношение для каждой пары дуг таких, что конец первой совпадает с началом второй, существует дуга, соединяющая начало первой дуги с концом второй.
Специальные бинарные отношения:
1) Отношение Эквивалентности на множестве А это отношение, обладающее свойством рефлекисвности, симметричности и транзитивности. (Отношение равенства, отношение параллельности).
2) Отношения строгого порядка: это бинарное отношение на множестве А, обладающее свойствами антирефлексивности, антисимметричности и транзитивности.
3) Отношения нестрого порядка- бинарные отношения, обладающие свойствами рефлексивности. Антисимметричности и транзитивности.
Множество M, на котором задано отношение частичного порядка, называется частично упорядоченным. Если быть совсем точным, то частично упорядоченным множеством называется пара
, где M — множество, а 
— отношение частичного порядка на M.26. Граф. Ориентируемый граф.
Ориентированный граф (или сокращенно орграф) G = (V, Е) состоит из множества вершин V и множества дуг Е. Вершины также называют узлами, а дуги – ориентированными ребрами. Дуга представима в виде упорядоченной пары вершин (v, w), где вершина v называется началом, a w – концом дуги. Дугу (v, w) часто записывают как v → w и изображают в виде
Ориентированный граф –граф вершины которого соединены дугами
27. Отношение эквивалентности. Классы эквивалентности. Разбиение множеств.
Бинарное отношение называется Отношение эквивалентности если оно рефлексивно симметрично транзитивно. обозначение .
Классом эквивалентностиMa
называется множество всех элементовM, находящихся в отношенииRк элементуa, то есть множество
Ma={x∈M:xRa}.
Пример
Пусть M — множество всех жителей России и R — отношение эквивалентности «проживать в одном городе». Найти классы эквивалентных элементов Ma для a∈M.
Класс элементов, эквивалентных элементу a, имеет вид:
Ma={x∈M:x проживает в одном городе с человеком a}
28. Сравнения. Вычеты. Множество классов вычетов по модулю n. Сложение и умножение классов вычетов по модулю n.
Сравнение по модулю Определение. Число a делится на натуральное b с остатком r, если a = bk + r, причем 0 6 r < b и k ∈ Z . Чтобынайтиостатокучисла a приделениина b, нужно из a вычесть ближайшее число, не превосходящее a, делящееся на b.
Сравнение - Целые числа, разность которых делится на m, называются сравнимыми по модулю m. Запись: a ≡ b (mod m).
Свойства сравнений. 1. a ≡ b (mod m) ⇔числа a и b даютодинаковыеостаткипомодулю m. Замечание. Несмотря на это свойство, если вы хотите проверить сравнимы ли два числа по модулю, то чаще всего удобнее рассматривать их разность, а не пытаться найти остатки для каждого. 2. a ≡ b (mod m), c ≡ d (mod m) ⇒ a + c ≡ b + d (mod m).
При делении целых чисел на натуральное число m существует m различ- ных остатков: 0, 1, 2,…, m – 1.
Соответственно этим остаткам Z разбивается на m непересекающихся классов сравнимых друг с другом чисел,
имеющих,один и тот же остаток от деления на m. В соответствии с остат-
ками от деления на m будем обозначать эти классы 0 , 1,…, m - 1. Таким обра- зом, класс i = { m * q + i | q э Z}
для каждого i = 0, 1, 2,…, m – 1. Любой пред- ставитель класса однозначно определяет свой класс, т. е. для каждого
m *q + i класс m * q + i= i .
Поскольку английское residue – «остаток» – переводится на русский язык еще и как «вычет»,
то множество всех классов сравнимых друг с другом чисел по модулю m называют множеством
классов вычетов по модулю m и обозна- чают Z/mZ.
Кольцом называется (непустое) множество K, на котором определены две операции (сложение и умножение), обладающие следующими свойствами:
1) множество K относительно сложения образует коммутативную группу;
2) умножение ассоциативно: для любых а, b, с ∈K
(ab)c = a(bc);
3) сложение и умножение подчиняются дистрибутивному закону:
(а + b)с = ас + bc, с(а + b) = са + сb
для любых а, b, с ∈K.
При этом множество K, рассматриваемое лишь относительно операции сложения, называется аддитивной группой кольца.
Приведем некоторые примеры колец.
. Множество целых чисел с операциями сложения и умножения - кольцо целых чисел Z.
. Множество многочленов от одного неизвестного с действительными коэффициентами с операциями сложения и умножения многочленов - кольцо многочленов R[X].
. Множество классов вычетов по модулю n с операциями сложения и умножения классов - кольцо классов вычетов Zn.
29. Функция. Область определения и область значений функции. Образ и прообраз подмножества. Композиция функций.
Фундаментальную роль в математике играет понятие функции (отображения), которое является частным случаем функционального отношения.
Определение 1.Бинарное отношение f между элементами множеств А и В (то есть
) называетсяфункциональным отношением,если 
из
и
Из определения 1 следует, что бинарное отношение является функциональным, когда каждому значению первой координаты пары из f соответствует единственная вторая координата, которая обозначается через y=f(x). И говорят в этом случае, что y является функцией от x.
Определение 2.
называетсяобластью определения функционального отношения.Определение 3.Функциональное отношение f между элементами множеств А и В называетсяфункциейилиотображениемА в В, если
и обозначается
Множество А называется областью определения функции, множество В -областью значения функции.
Если y=f(x), то y называетсяобразомпри отображении f точки x, а x называетсяпрообразомпри отображении f точки y.
Пусть
, тогда
называетсяобразом множества (подмножества)М при отображении f. В частности, 
образ множества А при отображенииf.Пусть
тогда
прообраз множества С при отображенииf. В частности, 
Композиция
Определение1.Пусть f и g – функции, причем g: A→B, f: B→C.Композицией(суперпозицией, произведением) функций f и g называется отображение A в C, значением которого для произвольного
служитf(g(x)).Обозначение:
или 
, то есть (fg)(x)=f(g(x)).Определение2.Отображение
и
называется равными тогда и только тогда, когдаf(x)=g(x) 
Пример:Пусть
и
– функции, определяемые следующим образом:
; g(x)=1–x. Тогда
; 
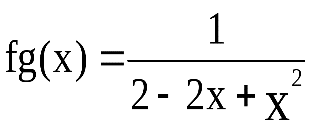Из примера видно, что
.Теорема1:Пусть
,
и
– отображения. Тогда 
и 
- отображенияA в D , причем 
(1), то есть произведения отображений ассоциативноДоказательство.
имеем:
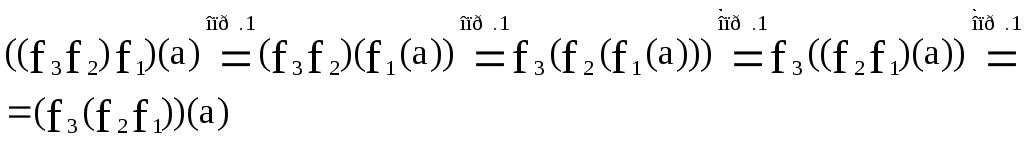
Следовательно, равенство (1) справедливо.Что и требовалось доказать.