ВОПРОСЫ и ответы К ЭКЗАМЕНУ. Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины

• Название: Ответы к экзамену комбинаторный признак умножения. Количество битовых строк длины
• Анкор: lbcrhtn vfnfy
• Дата: 10.05.2023
• Размер: 2.8 Mb.
• Имя файла: ВОПРОСЫ и ответы К ЭКЗАМЕНУ.docx
• Тип: Ответы к экзамену; #1120624
• страница: 5 из 6

30. Биекция и перестановка. Обратная функция.

Бие́кция—отображение, которое является одновременно исюръективным, иинъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют такжевзаимно однозначным отображением(соответствием).

Биективное отображение, являющеесягомоморфизмом, называютизоморфнымсоответствием.

Перестановкой из n элементов называется последовательность состоящая из всех элементов некоторого n-‘элементного множества причем число элементов этой последовательности равно n.

Обратной называется такая функция, для которой каждое ее значение (переменная y) определяется одним значением независимой переменной x из некоторого заданного множества X.

В алгебре принято следующее обозначение обратной функции:

Отметим, что не всякая функция является обратимой. Например, к квадратичной зависимости типаневозможно найти обратную функцию, так как два значения независимой переменной x задают одно значение переменной y.

Если теперь ограничить множество возможных значений аргумента интервалом, обратной функцией к исходной параболе станет функция видаСуществование обратной функции стало возможным, поскольку теперь аргумент может принимать только положительные значения.

Сформулируем необходимое условие обратимости функции.

К функции f(x) можно найти обратную тогда и только тогда, когда соблюдено каждое из представленных условий:

• 
  f(x)— непрерывно возрастающая или убывающая на заданной области допустимых значений X;
  
• 
  одно значение переменной x задает только одно значение переменной y.
  

31. Числовые матрицы. Операции над матрицами.

Матрицей называется таблица чисел (выражений), имеющая m строк и n столбцов

Если матрица содержит 1 строку и n столбцов, то она называется матрицей-строкой

Если матрица содержит m строк и 1 столбец, то она называется матрицей-столбцом.

Матрица, у которой совпадает количество столбцов с количеством строк, называется квадратной.

Транспонированной к исходной квадратной матрице называется такая матрица, строки которой заменены на соответствующие столбцы, а столбцы - на соответствующие строки.

Матрицу, у которой все элементы, стоящие под главной диагональю равны нулю, будем называть треугольной

Матрица, все элементы которой равны нулю, за исключением элементов, стоящих на главной диагонали,

Суммой (разностью) двух матриц   и   одинаковой структуры называется матрица той же размерности   элементы которой вычисляются по формуле: 



32. Матричное представление отношения. Булева матрица. Булевы операции над Булевыми матрицами.
Булевой матрицей (Boolean matrix) называется матрица, элементы которой принимают двоичные значения, т.е. 0 или 1.
 Матрицей бинарного отношения P называется матрица ||P||=(p_ij) размерности n x m, где n=|A|, m=|B|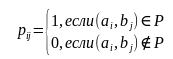



Если R являетсядвоичным отношениеммежду конечнымииндексированными наборами X и Y (так что R⊆X × Y), то R может быть представлен логической матрицей M, чьи индексы строки и столбца индексируют элементы X и Y соответственно, так что элементы M определяются как: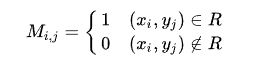



Для обозначения номеров строк и столбцов матрицы наборы X и Y индексируются положительными целыми числами: i варьируется от 1 до мощности (размер) X и j варьируется от 1 с числом элементов Y. Подробнее см. запись в индексированных наборах.

ЕслиG – граф (ориентированный или нет) без кратных дуг, то его матрица смежностиA являетсябулевой, то есть состоит из нулей и единиц. Для произвольной матрицыX = (xij) с неотрицательными элементами будем обозначать через sign(X) булеву матрицу, полученную изX заменой всех ее положительных элементов единицами. Например,

	1	2	0		1	1	0
sign	0	2	1	=	0	1	1	.
3		0	1	1		0	1

Равенство sign(X) =X означает, что матрицаX булева. Легко видеть, что

sign(X+Y) = sign(sign(X) + sign(Y)),

sign(X·Y) = sign(sign(X)·sign(Y))

в случае, когдаX иY неотрицательные матрицы, для которых определены соответствующие матричные операции. Далее, если матрицыX иY имеют одинаковую размерность, то

sign(X+Y) = sign(X) sign(Y) (дизъюнкция булевых матриц вычисляется поэлементно).

ПустьA иB – булевы матрицы. Матрицу sign(A·B) будем называть ихбулевым произведениеми обозначать черезAB. В

соответствии с определением sign(A·B) =AB. ЕслиA = (aij) и

B = (bij), то элементы булева произведенияAB = (cij) определяются формулами

cij = ai1b1j = ai2b2j … ainbnj ,

гдеn – число столбцов матрицыA и число строк ПоложимA[k]= sign(Ak) и будем называть матрицу степенью матрицыA.

матрицыB.A[k]булевой

ЕслиA – матрица смежности графаG, то на месте (i,j) матрицыA[k]находится 1, если на графеG существует путь длиныk изi вj, и 0 в противном случае. Пустьn – число вершин графаG. Тогда матрица

EAA[k]… A[n–1]

содержит 1 на месте (i,j) в том и только том случае, когда на графеG имеется хотя бы один путь из вершиныi в вершинуj.


33. Мощность. Счетные множества.

Определение 1.ПустьN- множество натуральных чисел. Множество S называется счётным множеством, если оно равномощно N, то есть S N.

Мощность конечного множества А называется число элементов этого множества.

Все счетные множества имеют мощность равную мощности натурального ряда чисел

Мощность натурального ряда чисел обозначается алеф-нуль.
34. Несчетные множества. Несчетность множества

действительных чисел R (с доказательством).
Несчётное мно́жество — бесконечное множество, не являющееся счётным.

• 
  не существуетинъективногоотображения� вомножество натуральных чисел� ;
  
• 
  �  непустое, и для каждой нумерованной последовательности элементов� существует по крайней мере один элемент� , не входящий в неё;
  
  • 
    иными словами:� непусто, и не существуетсюръективногоотображения множества натуральных чисел� на� ;
    
• 
  мощность� не является ни конечной, ни равнойℵ0 .
  

Данные определения являются эквивалентными всистеме Цермело— Френкелябез использованияаксиомы выбора. Доказательство эквивалентности данных определений со следующим:

• 
  мощность �  строго превышает ℵ0
  

— требует привлечения аксиомы выбора.

Надмножество несчётного множества несчётно. Простейший пример несчётного множества—континуум, вопрос о существовании несчётных множеств с мощностью менее мощности континуума составляет содержаниеконтинуум-гипотезы.

 Теорема 2.Любой отрезок множества действительных чисел состоит из несчетного множества точек.

Доказательство:Пусть это не так, тогда все точки отрезка[a, b], a<bможно пронумеровать,[a, b]={x₁,x₂…}. Выберем отрезок[a₁, b₁][a, b]не содержащийх₁. Таким образом если выбрать отрезок[a_n, b_n]то дальше выберем отрезок[a_n+1, b_n+1]. Продолжая этот процесс получим систему вложенных отрезков[a_n, b_n]такую чтоx_nне принадлежит[a_n, b_n], следовательно ни одна точка не принадлежит пересечению   [a_n, b_n]но согласно принципу вложенных отрезков существует точкаξпринадлежащая всем отрезкам. Следовательноξпринадлежит[a, b].

Теорема 3.(Кантор).Множество всех действительных чисел несчетно.

Доказательство: Если бы множество всех действительных чисел было бы счетно, то было бы счетно любое его подмножество и любой отрезок что противоречит теореме счетности рациональных чисел(Т1) и несчетности любых отрезков(Т2).
35. Мажоранты для функций.


36. Оценка числа операций, необходимых для сложения и умножения двух матриц, для вычисления значения многочлена.

алгоритм сложения матриц. Сложение матриц выполняется для каждого / и каждого у. Поскольку / принимает t значений, a j принимает p значений, то выполняется tp операций сложения. Пусть N= max {/и, п). Тогда число выполняемых арифметических операций имеет порядок 0(7V²);
алгоритм умножения матрицы Л размера т х р на матрицу В размера р х п. Поскольку к принимает значения от 1 до р, то выполняется р операций сложения и р операций умножения. Величина к изменяется от 1 до р для каждого / и каждого у, поэтому к пробегает значения от 1 до р тп раз. Таким образом, выполняется тпр операций сложения и тпр операций умножения. Следовательно, всего выполняется 2тпр операций. Пусть N = = max{/n, п, р}. Тогда число выполняемых арифметических операций имеет порядок 0(N³);

37. Алгоритм сортировки выбором (СВ). Пример. Оценка числа операций.

Сортировка выбором — это алгоритм сортировки массивов, в котором на каждой итерации во всей последовательности неотсортированных данных выбирается минимальный элемент (при сортировке по возрастанию) и помещается в первую позицию неотсортированной последовательности. Тем самым готовая (отсортированная) последовательность увеличивается на один элемент, а исходная (неотсортированная) последовательность на один элемент уменьшается.

Оценка - сортировка выбором. Рассмотрим число сравнений в процедуре СВ для списка из п элементов. Первый элемент сравнивается с остальными элементами и так далее до ( 1)-го элемента, который сравнивается только с одним элементом. Таким образом, (п 1) + (п 2) + ... + 2 + 1 = я(я 1)/2, так что число сравнений имеет порядок 0(и²);

function selectionSort(T[n] a):

for i = 0 to n - 2

for j = i + 1 to n - 1

if a[i] > a[j]

swap(a[i], a[j])
38. Граф и подграф. Основные понятия.
Графом называется система объектов произвольной природы (вершин) и связок (ребер), соединяющих некоторые пары этих объектов.

Подграфом графа G(V,E) называется граф, все вершины и ребра которого содержатся среди вершин и ребер исходного графа G(V,E).

Определим некоторые операции на графах.

Удаление или добавление ребра.

Удаление вершины. Из множества вершин удаляем выбранную вершину, а из множества ребер все инцидентные ей ребра.

Стягивание ребра. Отождествляем (стягиваем) вершины инцидентные выбранному ребру.

Добавление вершины (разбиение ребра). Выберем некоторое ребро (u,v) из множества ребер и удалим его. В множество вершин добавим новую вершину w, а в множество ребер новые ребра (u,w) и (w,v).

39. Орграф, мультиграф, размеченный граф. Основные понятия. Пути, связность.

Ориентированный граф (или сокращенно орграф)G = (V,Е) состоит из множества вершинV и множества дугЕ. Вершины также называют узлами, а дуги – ориентированными ребрами. Дуга представима в виде упорядоченной пары вершин (v,w), где вершинаv называется началом, a w – концом дуги. Дугу (v,w) часто записывают какv →w и изображают в виде

Говорят также, что дугаv →w ведет от вершиныv к вершинеw, а вершинаw смежная с вершинойv.

Нарис. 5.1показан орграф с четырьмя вершинами и пятью дугами.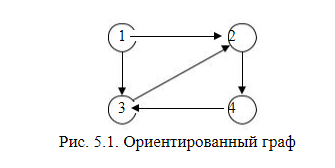



Маршрутом длиныиз в в орграфе называется последовательность рёбер вида



т.е. вторая вершина каждого ребра совпадает с первой вершиной следующего ребра. //

Часто удобно представлять маршрут последовательностью вершин



которые его определяют. Если   , то маршрут называютзамкнутым маршрутомилициклом. Орграф без циклов называютацикличным.

Мультиграф — граф, в котором может быть пара вершин, которая соединена более чем одним ребром (ненаправленным), либо более чем двумя дугами противоположных направлений.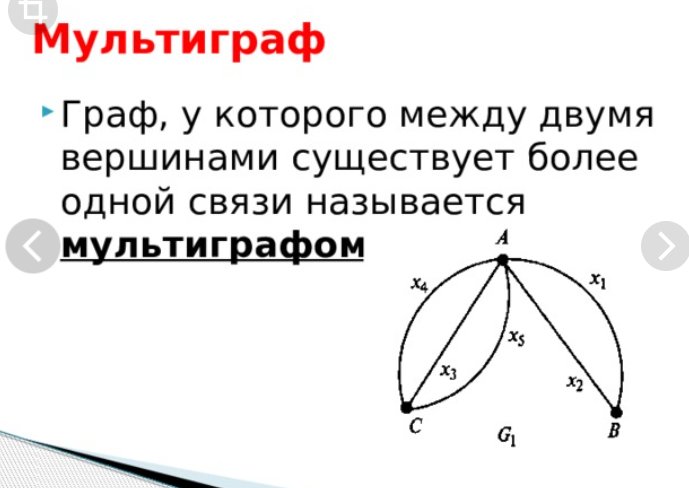


Размеченныйграф- этоориентированныйилинеориентированный граф G= (V, E), снабженный одной или двумя функциями разметки вида: l: V -> M и c: E -> L, где M и L - множества меток вершин и ребер, соответственно.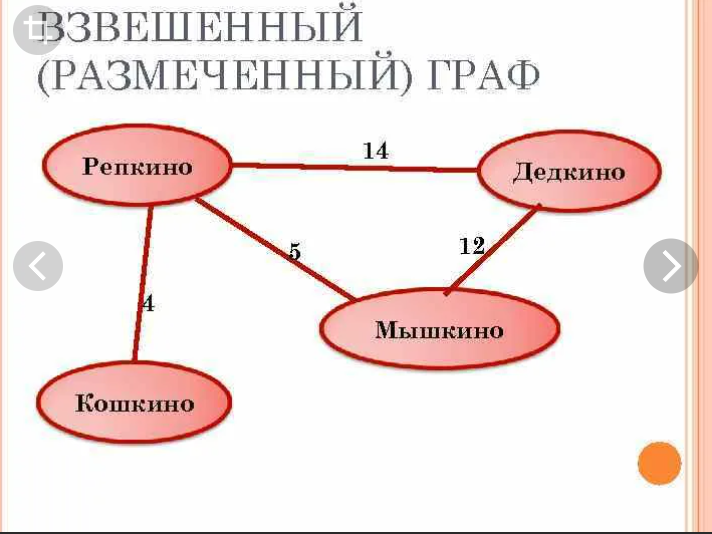



40. Деревья, ориентированные деревья.

Ориентированным деревом называют бесконтурный ориентированный граф, у которого полустепень захода любой вершины не больше 1 и существует ровно одна вершина, называемая корнем ориентированного дерева, полустепень захода которой равна 0.





Опираясь на данное определение, можно доказать, что в ориентированном дереве любая вершина достижима из корня.





Отметим, что из определения 5.6 нельзя убрать требование бесконтурности ориентированного графа, поскольку бесконтурность не вытекает из других условий. Например, на рис. 5.13 изображен ориентированный граф, не являющийся ориентированным деревом, хотя полустепени захода всех вершин не больше 1 и ровно одна вершина имеет полустепень захода, равную 0.





Определение 5.7.Вершину v ориентированного дерева называют потомком (подлинным потомком) вершины, если существует путь изв(путь ненулевой длины изв). В этом же случае вершинуназывают предком (подлинным предком) вершины, а если длина пути извравна 1, то вершинуназывают сыном вершины, которая при этом вполне естественно именуется отцом вершины. Вершину, не имеющую потомков, называют листом.
41. Корневые деревья. Остовное дерево графа.

Дерево – это граф без циклов.

Дерево называетсякорневым, если оно ориентированно, и из какой-то вершины (называемойкорнем) можно попасть во все остальные.

Примеры корневых деревьев:

• 
  наследование классов в языках программирования (если множественное наследование запрещено),
  
• 
  дерево факторизации числа на простые (в общем случае не уникальное),
  
• 
  иерархия в какой-нибудь организации,
  
• 
  дерево парсинга математичеких выражений.
  

Задачи на корневые деревья весьма бесполезны в реальной жизни, но зато очень интересны с алгоритмической точки зрения, и поэтому часто встречаются на олимпиадах по программированию.

О́стовное де́рево графа (англ. Spanning tree) — это дерево, подграф данного графа, с тем же числом вершин, что и у исходного графа. Неформально говоря, остовное дерево получается из исходного графа удалением максимального числа рёбер, входящих в циклы, но без нарушения связности графа. Остовное дерево включает в себя все � вершин исходного графа и содержит �−1ребро.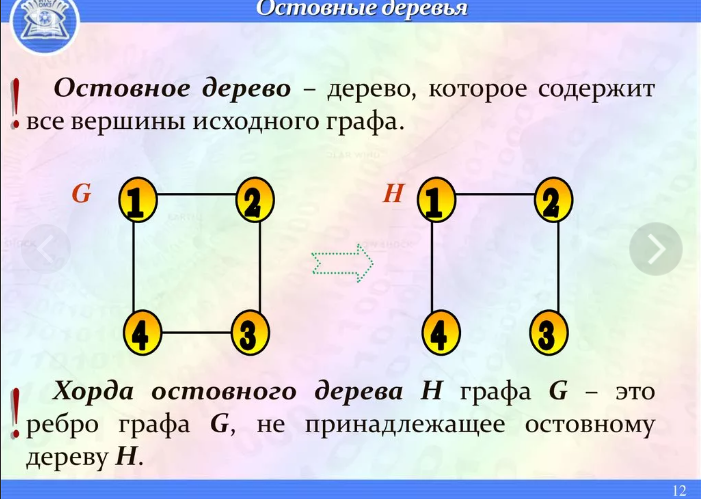


42. Две задачи о Кенигсбергских мостах. Пути и цели Эйлера.

Задача состояла в следующем: найти маршрут прохожде­ния всех четырех частей суши, который начинался бы с любой из них, кончался бы на этой же части и ровно один раз проходил по каждому мосту. Легко, конечно, попытаться решить эту задачу эмпирически, производя перебор всех маршрутов, но все попытки окончатся неудачей.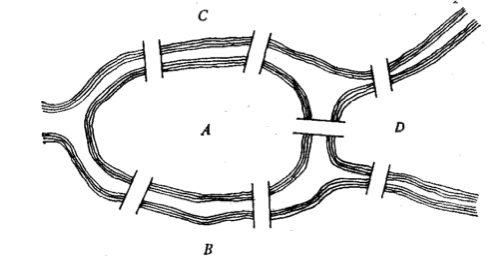



Исключительный вклад Эйлера в решение этой задачи заключается в том, что он доказал невозможность та­кого маршрута.

Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост – линией (ребром), соединяющей соответствующие точки. Получился граф. Утверждение о несуществовании положительного решения у этой задачи эквивалентно утверждению о невозможности обойти специальным образом данный граф.

ПустьG(V,E) – граф. Цикл, который включает все ребра и вершины графаG, называетсяэйлеровым циклом. Граф, в котором существует эйлеров цикл называетсяэйлеровым.

Связный граф является эйлеровым тогда и только тогда, когда степень каждой его вершины четная.

Определение 10.2.ПустьG(V,E) – граф. Путь, который включает каждое ребро графаGтолько один раз называетсяэйлеровым путем. Эйлеров путь, который не является циклом называетсясобственным эйлеровым путем.

Сформулируем теорему (без доказательства), в которой описано условие, при котором граф имеет собственный эйлеров путь.

Теорема 10.2.Граф (мультиграф или псевдограф) имеет собственный эйлеров путь тогда и только тогда, когда он связный и ровно две его вершины имеют нечетную степень.

По этой теореме получается, что задача о кенигсбергских мостах так же не имеет и эйлерова пути.

Аналогично можно ввести понятие эйлерова цикла для ориентированного графа и условие существования эйлерова цикла в орграфе.

Определение 10.3.ПустьG(V,E) - ориентированный граф. Ориентированный цикл, который включает все ребра и вершины графаG, называетсяэйлеровым циклом.

Теорема 10.3.Ориентированный граф имеет эйлеров цикл тогда и только тогда, когда он связный и полустепень захода каждой вершины равна ее полустепени исхода.
43. Матрица инцидентности и матрица смежности. Теоремы о к-путях.

Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро (дуга) и вершина). В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.
Матрица смежности - это вид представления графа в виде матрицы, когда пересечение столбцов и строк задаёт дуги. Используя матрицу смежности, можно задать вес дуг и ориентацию. Каждая строка и столбец матрицы соответствуют вершинам, номер строки соответствует вершине, из которой выходит дуга, а номер столбца - в какую входит дуга.
Если между двумя вершинами графа существует путь, то между ними существует вершинно-простой путь.

44. Алгоритм Уоршолла.

Алгоритм Флойда – Уоршелла – динамический алгоритм вычисления значений кратчайших путей для каждой из вершин графа. Метод работает на взвешенных графах, с положительными и отрицательными весами ребер, но без отрицательных циклов, являясь, таким образом, более общим в сравнении с алгоритмом Дейкстры, т. к. последний не работает с отрицательными весами ребер, и к тому же классическая его реализация подразумевает определение оптимальных расстояний от одной вершины до всех остальных.

45. Гиперкубы. Построение кода Грея для к+1.

Правила построения кода Грея дляк +1 состоят в следующем.

• 
  1. Поместить 1 перед каждой вершиной в ^-списке ^-мерного куба. Вершины, смежные в /с-мерном кубе, с приставленной впереди 1 остаются смежными в(к +1)-мерном кубе.
  
• 
  2. Поместить 0 перед каждой вершиной в реверсированном ^-списке ^-мерного куба. Вершины, смежные в ^-мерном кубе, с приставленным впереди 0 остаются смежными в(к+ 1)-мерном кубе.
  
• 
  3. Разместить последовательность, сформированную в пункте 2, после последовательности, сформированной в пункте 1.
  
• 
  4. Каждая последовательная пара вершин в(к+ 1)-мерном списке(к+ 1)-мерного куба является смежной. Первая вершина(к +1)-списка также является смежной с последней вершиной списка.
  

Подсеткойпонимают граф, вершины которого заданы массивом размератхпи для которого две вершины, соседствующие в одной и той же строке или столбце массива, являются смежными как вершины графа. Возможно ли длят<2^кип<2¹построитьподграф(к+/)-мерного куба,

Гиперку́б— обобщениекубана случай с произвольным числом измерений.Гиперкубом размерностиΝназывается множество точек вΝ-мерном евклидовом пространстве, удовлетворяющее неравенствам∀�:−�2<��<�2, где�— длина ребра гиперкуба.

Также можно определить гиперкуб какдекартово произведениеΝравных отрезков.


46. Построение (m×n) – сетки с помощью кода Грея.

Для построениякода Грея выполним следующие шаги:

1. 
   исходя из мощности алфавита, определим размер nxm таблицы для построения кода Грея, где n – число строк, m – число столбцов таблицы. Для этого будем последовательно наращивать число столбцов и число строк, начиная с одной строки и одного столбца, каждый раз проверяя, не достигнут ли требуемый размер таблицы. При этом схема наращивания числа строк и столбцов будет определяться следующим образом: число столбцов на каждом шаге итерации равно или на 1 превышает число строк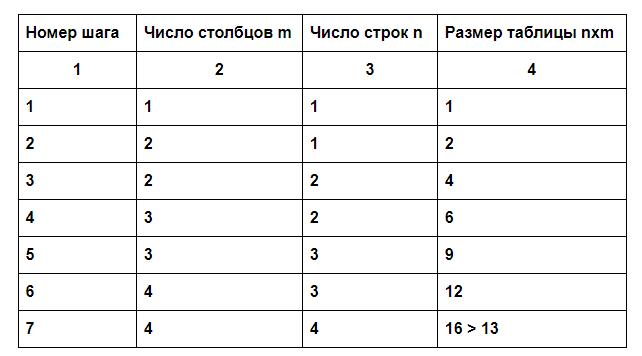
   
2. 
   
   

Поскольку на седьмом шаге итерации удалось достичь требуемого размера таблицы, определение ее размеров закончено. Таким образом, получена таблица размером 4х4,

2. 
   строки и столбцы таблицы пронумеруем двоичными числами из множества {00, 01, 10, 11}, элементы которого сами являются кодами Грея (затушеванные ячейки таблицы 4.2),
   

2. 
   разместим в ячейках таблицы упорядоченные по алфавиту символы исходного множества (см. графу 1 таблицы 4.3) в направлении, указанном стрелками в таблице 4.2,
   
3. 
   для формирования кода Грея по каждому символу объединим номера строки и столбца ячейки, в которой находится символ. Получим графу 2 таблицы 4.3.
   

47. Гомоморфизм, изоморфизм и гомеоморфизм графа.

Определение 5.14.Отображениемножества вершин графав множество вершин графаназывают гомоморфизмом графов (графав граф), если для любых двух вершин, смежных в первом графе, их образы при отображениисмежны во втором графе, т.е. если


Биективный гомоморфизм, такой, что любые две вершины смежны в первом графе тогда и только тогда, когда их образы смежны во втором графе, т.е.



называют изоморфизмом графови(графана граф), а графыи— изоморфными, что записывают в виде

Два графа G  и G’ гомеоморфны, если существует изоморфизм некоторого подразделения графа G и некоторого подразделения графа G’. Если рёбра графа понимать как отрезки, соединяющие вершины (как обычно рисуется на иллюстрациях), то два графа гомеоморфны в контексте теории графов, когда они гомеоморфны в топологическом смысле.


48. Объединение, пересечение, дополнение графов.
Пересечение (произведение) графовПересечением графов G1(X₁,Г₁X₁) и G2(X₂,Г₂X₂) называется такой граф G(X,ГX), у которого множество вершин есть пересечение множеств вершин графов X=X₁ÇX₂, а отображение есть пересечение отображений перемножаемых графовГX=Г₁X₁ÇГ₂X₂.Пример.Пересечение графов G₁ и G₂ предыдущего примера есть граф G(X,ГX)



Объединением графов G₁(X₁,Г₁X₁) и G₂(X₂,Г₂X₂) называется такой граф G(X,ГX), у которого множество вершин есть сумма множеств вершин объединяемых графов X=X₁ÈX₂, а отображение есть сумма отображений объединяемых графовГX=Г₁X₁ÈГ₂X₂. обозначает: G=G₁ÈG₂.

Пример. Заданы графы G₁и G₂:

1. 
   Дополнениемграфа G₁(V₁,E₁) называется граф G₂(V₂,E₂), у которого множество вершин такое же, как у исходного графа, а множество ребер представляет собой дополнение до множества   Вершины графа G₂смежны только в том случае, когда они не смежны в исходном графе. Обозначение: ` G₁(V₁,E₁). Дополнение графов есть дополнение
   

Дополнение к полному графу – пустой граф. Другой пример показан на рисунке.


49. Разрезающее множество, разрезающее ребро и разрезающая вершина графа.

К Разрезающиму множеству S связного графа G относится такое минимальное множество ребер графа G что удаление их из графа G разделяет последний т.е г раф G-S становиться не связным.



 Ребро е графа G является разрезающим тогда и только тогда, когда оно не входит в цикл графа G.

Разрезающая вершина(Cutvertex (cuttingvertex)) —вершина   графа   такая, что после ее удаления множество   разбивается на непересекающиеся непустые подмножества   и  , между которыми нетреберграфа  .
50. Теоремы о компонентах двусвязности графа.

Компонентой двусвязности графа называется такое максимальное подмножество из трех или более его вершин, в котором любые две вершины соединены, по крайней мере, двумя путями, не имеющими общих ребер. 

 Кроме того компонента двусвязности может представлять собой просто две вершины, соединенные одним ребром. Компонента двусвязности - устойчивая часть графа: если в ней удалить вершину и все примыкающие к ней ребра, то любые две из оставшихся вершин по-прежнему оказываются соединенными между собой.

51. Планарные графы. Грани. Формула Эйлера.

Граф, который может быть изображенна плоскостибез пересечений рёбер, называетсяпланарным графом.

Например, граф

G({a,b,c,d},{{a,b}{a,c}{a,d}{b,c}{b,d}{c,d}})

можно изобразить и с пересечением и без пересечений рёбер, поэтому этот граф является планарным.



Если граф планарный и изображен на плоскости без пересечений рёбер, то диаграмма для графа разделяет плоскость на части, называемыегранями.Грань – максимальный участок плоскости, в котором две точки могут быть соединены линией (любой формы), не пересекающей ребро графа.



На рисунке три грани изображены треугольниками:1 – abc,2 – abd,3 – bcd. Грань4представляет собой внешнюю область плоскости.

Формула Эйлера. В связном планарном графе v − e + f = 2.
52. Теоремы о планарных и непланарных графах.

Если G связный плоский граф имеющий р –вершин и q- ребер и f –граней то p+f-q=2 данная теорема называется формулой эйлера

53. Непланарность графа Петерсона.



Т.к. в графе Петерсона степени всех вершин равны 3, найти подграф, гомеоморфный K5 , нельзя. Следовательно, существует подграф, гомеморфный K3,3 . Будем использовать следующий образец для выбора вершин на роль вершин одной доли (1, 2, 3) и на роль вершин второй доли (4, 5, 6).

54. Гамильтонов путь и Гамильтонов цикл. Теоремы о Гамильтоновых циклах.

Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл называется гамильтоновым циклом, а граф называется гамильтоновым графом. Граф, который содержит простой путь, проходящий через каждую его вершину, называется полугамильтоновым. Это определение можно распространить на ориентированные графы, если путь считать ориентированным.

Гамильтовым путем называется граф проходящий через каждую его вершину только один раз.

Теорема Дирака. Если в графе G(V, E) с p ≥ 3 вершинами ∀v ∈ V d(v) ≥ p/2, то граф G является гамильтоновым. Доказательство. Пусть V = {v1, . . . , vp}. Заметим сначала, что любой граф можно превратить в гамильтонов добавлением в него p дополнительных вершин степени 2: вместе с дополнительной вершиной ui , где i = 1, . . . , p − 1 добавляются ребра (vi , ui) и (ui , vi+1), вместе с вершиной up – ребра (vp, up) и (up, v1). Тогда гамильтонов цикл имеет вид:

v1u1v2u2 . . . vpupv1.
55. Замыкание графа. Примеры.



ПРИМЕР



56. Взвешенные графы. Алгоритм Дейкстры.