2-файл. Что такое функция

• Название: Что такое функция
• Дата: 25.10.2021
• Размер: 0.5 Mb.
• Имя файла: 2-файл.docx
• Тип: Документы; #255151

1. 
   Что такое функция?
   

Фу́нкция (отображе́ние, опера́тор, преобразова́ние) — в математике соответствие между элементами двух множеств, установленное по такому правилу, что каждому элементу первого множества соответствует один и только один элемент второго множества.

Функция – это соответствие между двумя множествами такое, что каждому элементу одного множества   ставится в соответствие единственный элемент другого множества  . Первое множество называют областью определения функции, а второе – областью значений функции. Обозначают:   и   соответственно.

Пример 1: задана функция, которая ставит в соответствие каждому человеку размер его обуви. Область определения функции   – множество людей, область значений функции   –  множество размеров обуви.

Пример 2: задана функция, которая ставит в соответствие каждому дню месяца среднюю температуру воздуха. Область определения функции   – множество дней месяца, область значений функции   –  множество температур 

2. 
   Способы задания функций
   

Числовые функции можно задавать разными способами.

1. 
   Аналитический.
   
2. 
   Графический.
   
3. 
   Табличный.
   

Аналитический способ — это способ задания функции с помощью формулы.

Например, формула  y = x - 2  показывает, как с помощью значения аргумента  x  вычислить соответствующее ему значение функции  y.

Табличный способ — это способ задания функции с помощью таблицы со значениями.

Например, если измерять температуру воздуха каждый час в течении суток, то каждому часу (t) будет соответствовать определённая температура (T). Такое соответствие можно записать в виде таблицы:

t (ч)	0	1	2	3	4	5	6	7	8	9	10	11
T (°)	14	14	14,5	14,5	15	15	16	16	16	16,5	16,5	17
t (ч)	12	13	14	15	16	17	18	19	20	21	22	23
T (°)	18	20	22	24	24,5	24,5	24	23	21	20	18	16

Следовательно,  T  функция от  t  —  T(t),  определённая с помощью множества целых чисел от  0  до  24  и заданная таблицей. Соответствие между величинами двух переменных задаётся в данном случае не формулой, а таблицей.

Графический способ — это способ задания функции с помощью графика. В этом случае аргумент является абсциссой точки, а значение функции, соответствующее данному аргументу, ординатой.

Графики позволяют быстро находить значение функции по значению аргумента и наоборот — значение аргумента по значению функции. Например, рассмотрим уже готовый график функции:



Чтобы узнать, какое значение функции будет соответствовать аргументу  x = 1,  надо провести из соответствующей точки оси абсцисс (оси  x) перпендикуляр на график. Ордината точки пересечения перпендикуляра с графиком (точки  M) и будет соответствующим значением функции. Поэтому, так как точка  M  имеет координаты (1; 2), то запись этих значений в виде функции будет выглядеть так:  y(1) = 2.

3. 
   Какие элементарные функции вы знаете?
   

1)Показательная функция y = α^x,a>0, a 1; Рис.1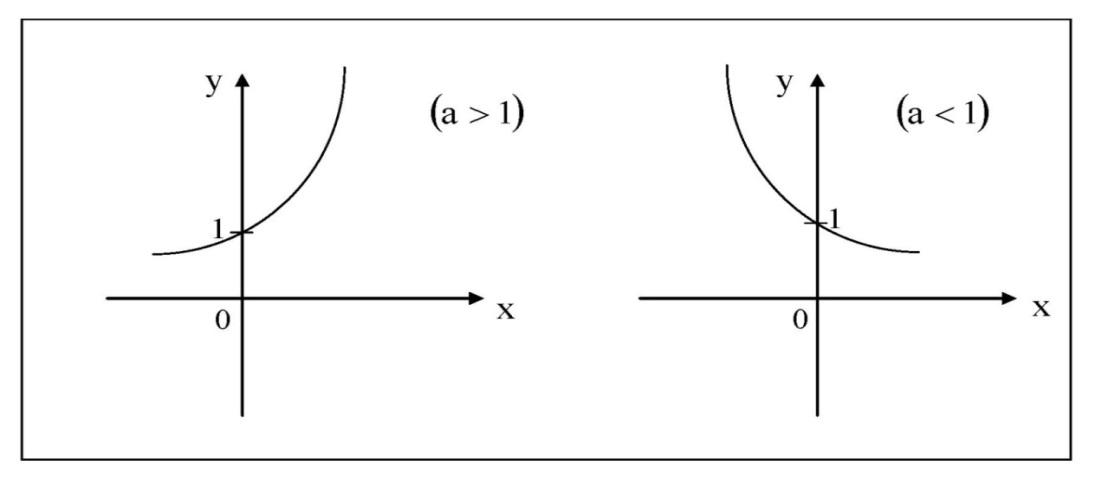



2) Степенная функция y = x^α, α∈R .

Графики степенных функций, соответствующих различным показателям степени, представлены на рис. 2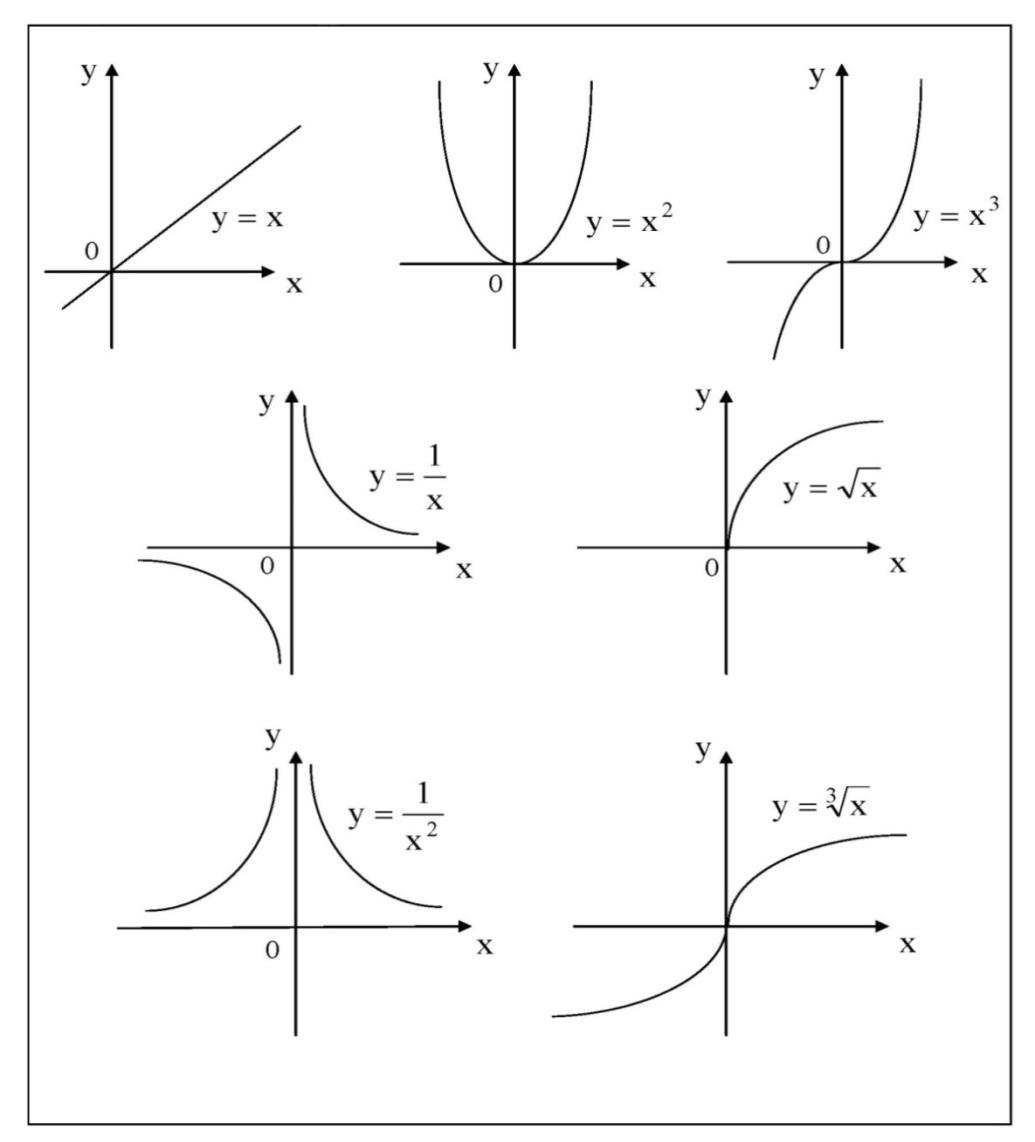



3) Логарифмическая функция  y = log_ax, a>0, a 1;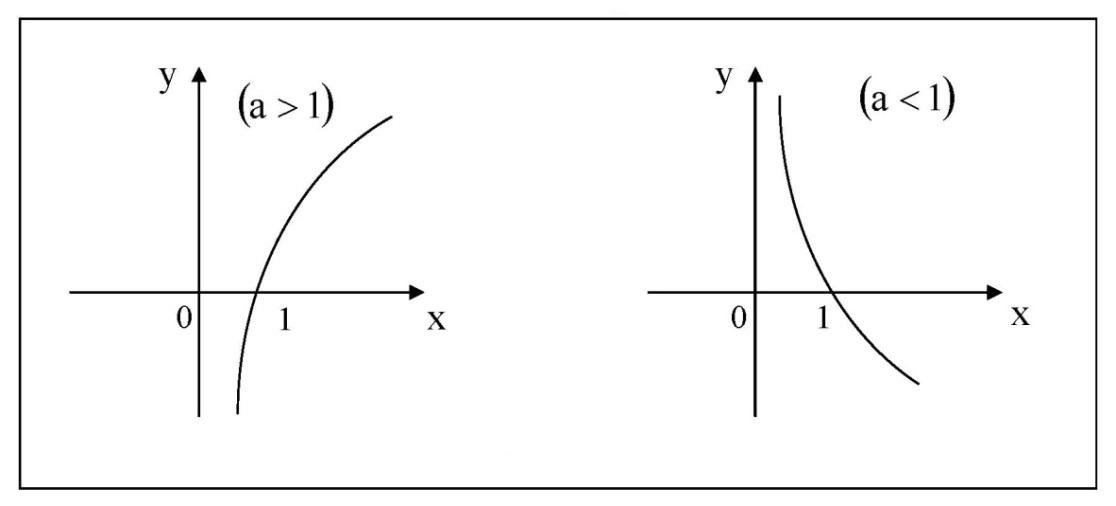

+

Рис. 3

4) Тригонометрические функции

y = sinx, y = cosx,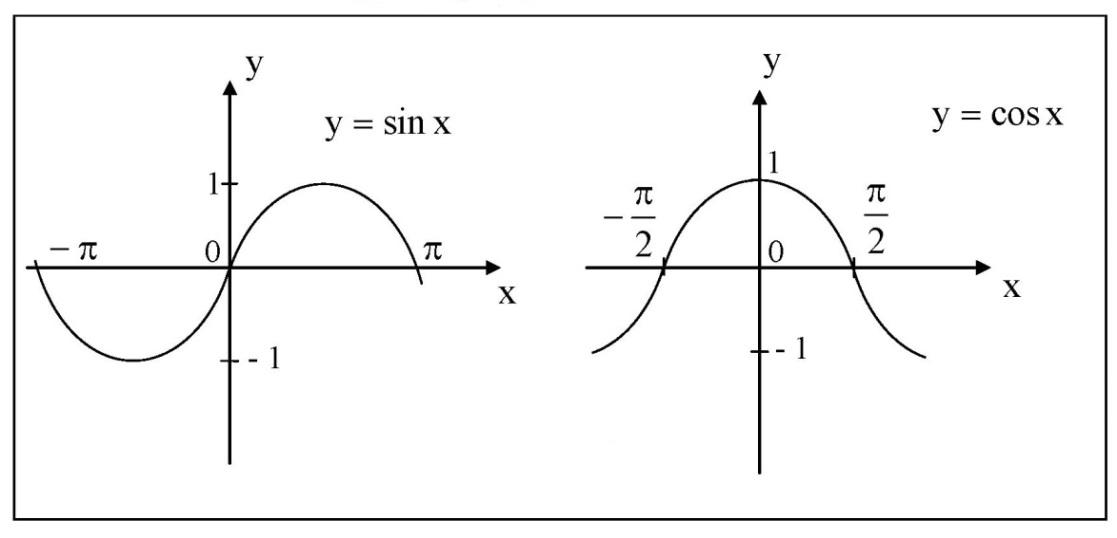



Рис. 4

y = tgx, y = ctgx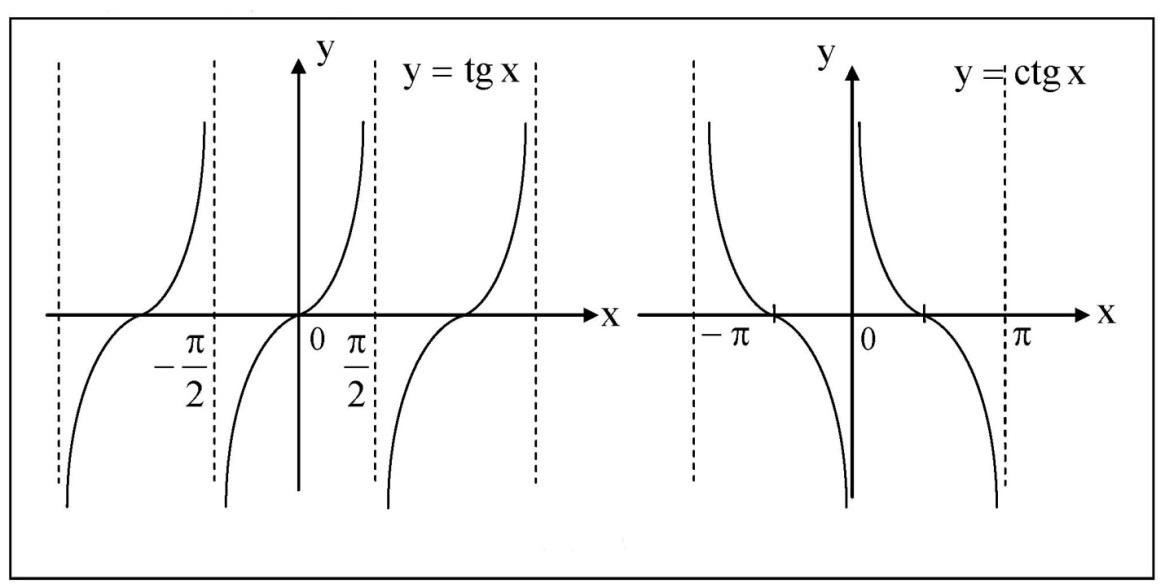



Рис. 5

5) Обратные тригонометрические функции 

y=arcsinx, D (f) = [-1; 1], E (f) = ;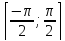

y = arccos x, D (f ) = [- 1; l], E (f) =  ;

y = arctg x, D (f) = R, E (f) = ;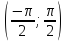

y = arcctg x, D (f) = R, E (f) =

4.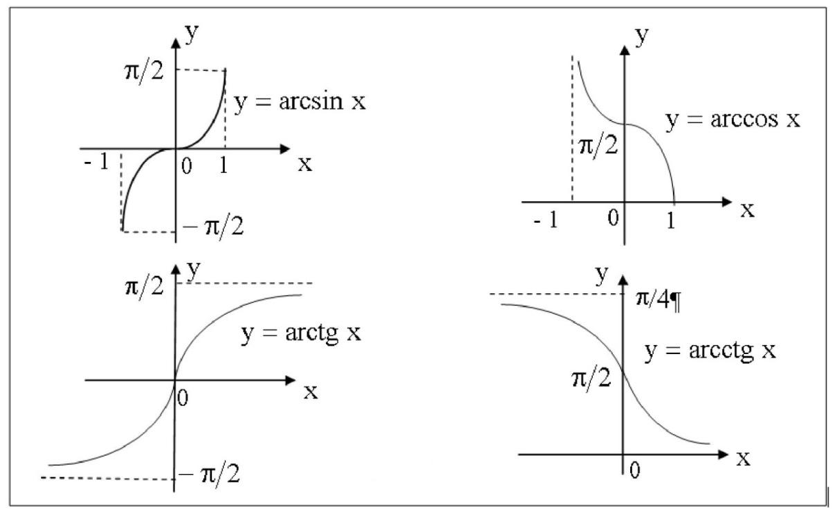 
   К
   акие функции называются четными (нечетными)?
   

Нечётная фу́нкция — это функция, меняющая знак при изменении знака независимого переменного. 

Чётная фу́нкция — это функция, не изменяющая своего значения при изменении знака независимого переменного. 

Определения

Функция

 

называется нечётной, если справедливо равенство



Функция   называется чётной, если выполнено равенство



Если не выполняется ни одно из этих равенств, то функция называется функцией общего вида.
Примеры

Нечётные функции

функции с нечетными степенями

.y=sin x, y=tg x, y=ctg x

Чётные функции

Чётная степень 

 

где 

 — произвольное целое число.

5. 
   Какие функции называются периодическими?
   

1. ЧислоT≠0называетсяпериодомфункции f, если вместе со всяким числомx∈D(f) числа х+Т и x-Т также принадлежат D(f) и выполняется равенство f(x+Т)=f(x).

2. Функция называетсяпериодической, если она имеет хотя бы один период.
Естественно, функцию называют периодической с периодом Т, если число Т является ее периодом.

Сама форма определения периода подсказывает, что периодов у функции может быть много: в нем подразумевается, что всякое число Т с указанным свойством является периодом функции f, а вы прекрасно знаете, что если Т — период f, то любое его кратное, т.е. число вида nТ, где n — любое целое число, является ее периодом.

В частности, поэтому некорректны, строго говоря, часто встречающиеся фразы типа «Периодом функции y=sinxy=sinx является 2π» — периодов у синуса много, и лишь один из них равен 2π. В то же время не может вызвать никаких возражений фраза — из те же слов, но в другом порядке: «2π является периодом функции y=sinxy=sinx».

6. 
   Дать определение убывающей функции
   

Функция     называется убывающей на интервале   , если

(Большему значению аргумента соответствует меньшее значение убывающей функции). 
      Имеется тесная взаимосвязь между поведением функции 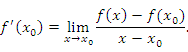    в некотором промежутке и знаком производной     в этом промежутке. Действительно, по определению производной,



Если 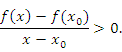  , то существует окрестность точки   , в которой разностное отношение под знаком предела остается положительным:



Тогда



и, следовательно, функция     является возрастающей в окрестности точки   . 

7. 
   Дать определение возрастающей функции
   

Функция     называется возрастающей на интервале   , если

Другими словами, большему значению аргумента соответствует большее значение функции. 

8. 
   Дана функция f(x)=x²+4x-5. Вычислить f(5)
   

f(5)=x²+4x-5=25+4•5-5=40

ответ: f(5)=40

9. 
   Свойства тригонометрических функций
   

Свойства синуса.

• 
  Область определения функции — множество всех действительных чисел: D(y)=R.
  
• 
  Множество значений — интрервал [−1; 1]: E(y) = [−1;1].
  
• 
  Функция y=sin(α) - нечетная: sin(−α)=−sinα.
  
• 
  Функция оказывается периодической, самый маленький неотрицательный период соответствует 2π: sin(α+2π)=sin(α).
  
• 
  График функции пересекает ось Ох при α=πn,n∈ Z.
  
• 
  Промежутки знакопостоянства: y>0 при (2πn+0;π+2πn),n∈Z и y<0 при (π+2πn;2π+2πn),n∈Z.
  
• 
  Функция является непрерывной и у нее есть производная с любым значением аргумента: (sinα)′=cosα.
  
• 
  Функция y=sinα возрастает при α∈(−π/2+2πn;π/2+2πn) n∈Z, и убывает при α∈(π2+2πn;3π2+2πn), n∈Z.
  
• 
  Минимум функции при α=−π/2+2πn, n∈Z, а максимум при α=π/2+2πn, n∈Z.
  

Свойства косинуса.

• 
  Область определения функции — множество всех действительных чисел: D(y)=R.
  
• 
  Множество значений — интервал [−1; 1]: E(y) = [−1;1].
  
• 
  Функция y=cos(α) - четная: cos(−α)=cosα.
  
• 
  Функция периодическая, самый маленький неотрицательный период соответствует 2π: cos(α+2π)=cos(α).
  
• 
  График функции пересекает ось Ох при α=π/2+πn,n∈Z.
  
• 
  Промежутки знакопостоянства: y>0 при (−π/2+2πn;π/2+2πn),n∈Z и y<0 при (π/2+2πn;3π/2+2πn),n∈Z.
  
• 
  Функция является непрерывной, у нее есть производная с любым значением аргумента: (cosα)′=−sinα.
  
• 
  Функция y=cosα возрастает при α∈(−π+2πn;2πn),n∈Z, и убывает при α∈(2πn;π+2πn),n∈Z.
  
• 
  У функции есть минимум при α=π+2πn,n∈Z, а максимум при α=2πn,n∈Z.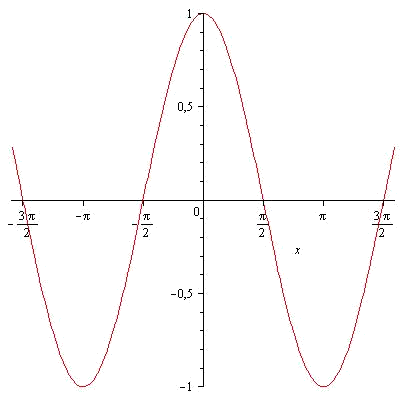
  

Свойства тангенса.

• 
  Область определения функции — множество действительных чисел: D(y)=R, исключая числа α=π/2+πn.
  
• 
  Множество значений — множество действительных чисел: E(y)=R.
  
• 
  Функция y=tg(α) - нечтная: tg(−α)=−tg α.
  
• 
  Функция оказывается периодической, самый маленький неотрицательный период соответствует π: tg(α+π)=tg(α).
  
• 
  График функции пересекает ось Ох при α=πn,n∈Z.
  
• 
  Промежутки знакопостоянства: y>0 при (πn;π/2+πn),n∈Z и y<0 при (−π/2+πn;πn),n∈Z.
  
• 
  Функция является непрерывной, есть производная с любым значением аргумента из области определения: (tgx)′=1/cos²x.
  
• 
  Функция y=tg α возрастает при α∈(−π/2+πn;π/2+πn),n∈Z.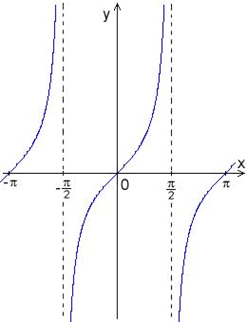
  

 



Свойства котангенса.

• 
  Область определения функции — множество действительных чисел: D(y)=R, исключая числа α=πn.
  
• 
  Множество значений — множество действительных чисел: E(y)=R.
  
• 
  Функция y=ctg(α) - нечетная: ctg(−α)=−ctg α.
  
• 
  Функция периодическая, самый маленький неотрицательный период равен π: ctg(α+π)=ctg(α).
  
• 
  График функции пересекает ось Ох при α=π/2+πn,n∈Z.
  
• 
  Промежутки знакопостоянства: y>0 при (πn;π/2+πn),n∈Z и y<0 при (π/2+πn;π(n+1)),n∈Z.
  
• 
  Функция является непрерывной, есть производная в любом значении аргумента из области определения: (ctgx)′=−1/sin²x.
  
• 
  Функция y=ctg α убывает при α∈(πn;π(n+1)),n∈Z.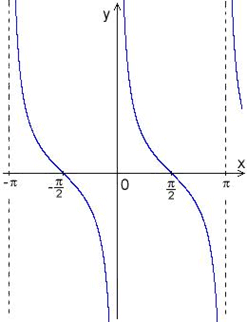
  

 

10. 
    Определить на четность данной функции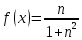
    

Функция общего вида. Не является ни чётной, ни нечётной