Проектирование привода к лесотаске. Аманбай Б ММГ-18-2Р ОКДМ. П роектирование привода
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
3.2. Проверочный расчет косозубых цилиндрических передач Проверочный расчет проводим в соответствии с ГОСТ 21354-87 1. Расчетная зависимость для проверки передачи на контактную выносливость зубьев имеет вид 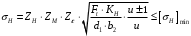 (16) (16)2. Определяем коэффициенты 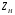 -коэффициент, учитывающих форму сопряженных поверхностей зубьев. -коэффициент, учитывающих форму сопряженных поверхностей зубьев.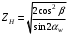 (17) (17)где 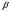 - угол наклона зубьев, - угол наклона зубьев, 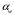 - угол зацепления. - угол зацепления.При коэффициенте смещения инструмента 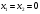 угол зацепления угол зацепления 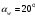 , ,Имеем 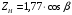 (18) (18)В нашем случае 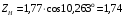 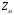 - коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, МПа1/2. - коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, МПа1/2.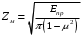 (19) (19)где: 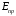 - приведённый модуль упругости; - приведённый модуль упругости; 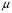 -коэффициент Пуассона, -коэффициент Пуассона, 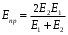 (20) (20)Для пары стальных колес имеем 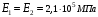 ; ;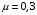 ,тогда ,тогда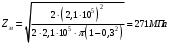 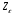 -коэффициент, учитывающий суммарную длину контактных линий. -коэффициент, учитывающий суммарную длину контактных линий.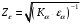 (21) (21)- для косозубых колес где – коэффициент торцового перекрытия зубьев. 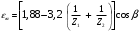 (22) (22)Z1; Z2 – числа зубьев, соответственно, шестерни и колеса; – делительный угол наклона зубьев К -коэффициент, учитывающий осевое перекрытие зубьев в косозубых передачах. Значение К принимаем в зависимости от 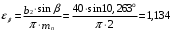 Принимаем К =0,95 Для зубьев колес, нарезанных без смещения режущего инструмента, при <200 коэффициент торцового перекрытия составляет 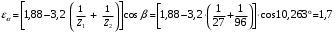 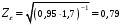 3. Окружная сила 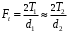 (23) (23)T1 и T2– крутящие моменты на шестерни и колесе соответственно. 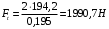 4. Коэффициент нагрузки 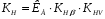 (24) (24)K А – коэффициент внешней динамической нагрузки; K HV – коэффициент динамичности нагрузки, возникающей в зацеплении взаимодействующих колёс передачи; K Hβ –коэффициент концентрации нагрузки по длине контактных линий зубьев. При равномерном режиме работы электродвигателя коэффициент K А выбирают в зависимости от режима работы рабочего органа: K А = 1,0 – равномерный режим. Определяем коэффициент концентрации нагрузки K Hβ Для прирабатывающихся зубьев колес (хотя бы одно из колес имеет твердость зубьев менее 350HB) при переменной нагрузке 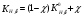 (25) (25)где 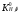 - коэффициент начальной концентрации нагрузки, выбираемый по таблице в зависимости от - коэффициент начальной концентрации нагрузки, выбираемый по таблице в зависимости от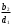 и расположения шестерни относительно опор вала; и расположения шестерни относительно опор вала;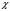 -коэффициент, учитывающий влияние переменного режима нагружения на степень прирабатываемости колёс. -коэффициент, учитывающий влияние переменного режима нагружения на степень прирабатываемости колёс.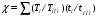 (26) (26)Здесь Ti, ti - крутящий момент и время его действия на i-й ступени блока нагружения. Тном – номинальный момент, t – срок службы передачи. В нашем случае 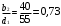 . Значит . Значит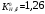 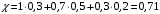 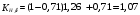 Определяем коэффициент динамичности нагрузки КНV. При таком значении скорости принимаем 9-ю степень точности. Тогда 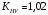 Коэффициент нагрузки 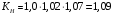 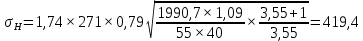 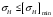 Недогрузка передачи составляет 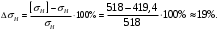 Величина 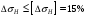 что недопустимо и указывает на возможность уменьшения габаритов передачи. что недопустимо и указывает на возможность уменьшения габаритов передачи.Изменим ширину зубчатых колес, примемψa=0.25. Тогдаa2=32 , a1=40 Уточняем коэффициент нагрузки 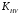 . При отношении . При отношении 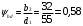 имеем 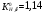 , тогда , тогда 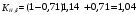 Коэффициент нагрузки 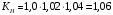 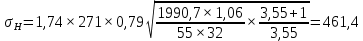 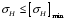 Проверяем передачу на изгибную выносливость зубьев 1. Запишем условие прочности по напряжениям изгиба для зубьев колеса и шестерни 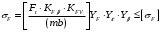 (27) (27)Пользуясь рекомендациями, считаем коэффициент концентрации нагрузки 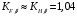 и коэффициент динамичности нагрузки и коэффициент динамичности нагрузки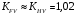 Коэффициент формы зуба 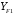 и и 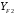 находим в зависимости от числа зубьев рассчитываемого колеса и коэффициента смещения режущего инструмента находим в зависимости от числа зубьев рассчитываемого колеса и коэффициента смещения режущего инструментаЭквивалентное число зубьев для косозубых колес 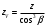 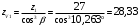 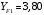 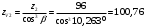 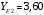 Коэффициент, учитывающий перекрытие зубьев: 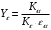 , где , где 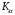 - коэффициент, учитывающий многопарность зацепления; - коэффициент, учитывающий многопарность зацепления;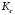 - коэффициент, учитывающий осевое перекрытие зубьев; - коэффициент, учитывающий осевое перекрытие зубьев; 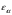 - коэффициент торцевого перекрытия. - коэффициент торцевого перекрытия.Для передач, применяемых в редукторостроении можно принимать 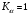 , тогда , тогда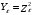 В нашем случае 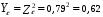 Коэффициент, учитывающий угол наклона зубьев: 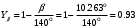 Условие прочности имеет вид 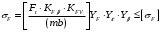 (28) (28)Допускаемые изгибные напряжения [σF]1=280, [σF]1=260 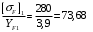 ; ;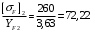 ; ;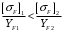 (29) (29)Следовательно, на изгибную выносливость проверяем зубья шестерни. 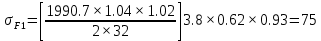 Допускается перегрузка 5% но, несмотря на значительную недогрузку уменьшать модуль и ширину колес нельзя. Проверяем передачу на прочность зубьев при пиковых перегрузках. 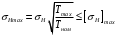 , (30) , (30)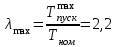 σH=461 Тогда. 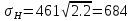 Следовательно, местная пластическая деформация зубьев будет отсутствовать. Проверим на изгибную прочность при пиковой перегрузке . 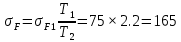 Объемная пластическая деформация зубьев будет отсутствовать 3.3 Геометрические характеристики зацепления Расчет геометрических характеристик передачи внешнего зацепления рассчитывают по ГОСТ 16532-70. Для рассчитываемой передачи имеем геометрические параметры:  , mn=2, d1=55; d1=195; b1=40, b2=32 aw=225 , mn=2, d1=55; d1=195; b1=40, b2=32 aw=225 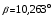 . .Определяем основные размеры шестерни и колеса. 1.Диаметры окружностей вершин зубьев: 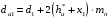 (31) (31)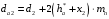 (32) (32)где 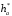 - коэффициент головки зуба исходного контура. - коэффициент головки зуба исходного контура.В соответствии с ГОСТ 13755-81 у исходного контура с 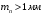 , имеем , имеем 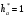 ; ;x– коэффициент смещения режущего инструмента. В нашем случае 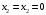 da1=55+2(1+0)×2=59 da1=195+2(1+0)×2=199 2.Диаметры впадин зубьев. 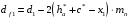 (32) (32)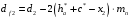 (33) (33)где 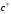 - коэффициент радиального зазора исходного контура - коэффициент радиального зазора исходного контураСогласно ГОСТ 13755-81 имеем 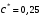 da1=55-2(1+0.25-0)×2=50 da1=195-2(1+0.25+0)×2=190 3.4 Расчёт валов. Расстояния 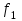 (мм) ведущего вала можно принимать по ориентировочной рекомендации [7, стр. 284] в зависимости от передаваемого момента: (мм) ведущего вала можно принимать по ориентировочной рекомендации [7, стр. 284] в зависимости от передаваемого момента: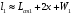 , (34) , (34)где 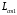 – длина ступицы колеса: – длина ступицы колеса:L1=b+(5+10) (35) 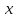 – зазор между зубчатыми колесами и внутренними стенками корпуса редуктора: – зазор между зубчатыми колесами и внутренними стенками корпуса редуктора: 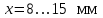 . В данном случае x=10 . В данном случае x=10W1=30; T1=56.1 H×мм; l1=100; 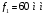 . f1=60 . f1=60 Рисунок 1-Расчетная схема быстроходного вала Определяем согласно расчетной схеме реакции опор в горизонтальной плоскости из условия равновесия: ΣMA=F1(l+f)-OAl-Ft1×l/2 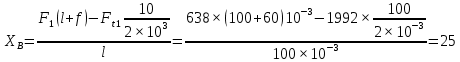 отсюда Первоначальное направление реакции ХВ выбрано верно. ΣMB=XAl+F 1f+Ft1×l/2=0 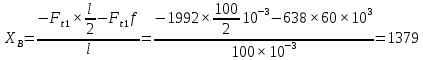 Проверка: 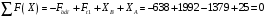 . .Определяем реакции опор в вертикальной плоскости из условия равновесия 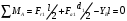 (37) (37)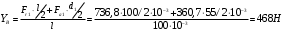 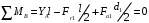 Проверка: 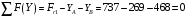 . .Радиальная нагрузка на опору А 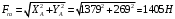 Радиальная нагрузка на опору В  Определяем изгибающие моменты в характерных сечениях вала: Изгибающие моменты в горизонтальной плоскости: - для среднего сечения шестерни I=Xa×l/2=-1379×.0,1/2=-69 - под подшипником В IB=Fa×f=638×.60×10-3=-38.3 - под подшипником А IA=0 - под звездочкой цепной передачи IA=0.5×IB=0.5×38.3=19.15 3.5 Подбор шпоночных соединений для быстроходного вала 1) Под звездочкой: d=25 мм, по ГОСТ 23360-78; b×h=7×8 t=4 Определим расчетную длину шпонки по формуле: 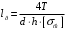 (38) (38)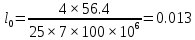 l=l0+b=13+8=22 3.6 Подбор шпоночных соединений для тихоходного вала 1) Под колесом: d=45 мм, по ГОСТ 23360-78 b×h=7×8 t=4 Определим расчетную длину шпонки: 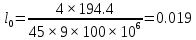 l=l0+b=19+14=33 3.7 Проверка быстроходного вала Определяем нормальные напряжения под шестерней, концентратор напряжений – галтель. 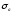 и и  - амплитуды напряжений цикла - амплитуды напряжений циклаσa=M/(0.1d3)=69/(0.1×0.033)=22.2 τa=0.5T/(0.2d3)=0.5×56.4/(0.2×0.033)=5.2 Эффективные коэффициенты концентрации нормальных К и касательных К напряжений для сечений с геометрическими источниками концентраций этих напряжений (галтели, канавки, проточки, шпоночные пазы и т.д.) определяют по таблицам ГОСТ 25.504 – 82 в зависимости от вида концентратора, его размеров и предела прочности в материала вала. 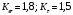 Масштабные факторы для вала d=30 мм по [7, стр. 292]: 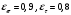 . . 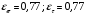 Коэффициенты, учитывающие влияние постоянной составляющей цикла для легированных сталей: 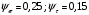 [7, стр. 292]. [7, стр. 292].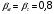 - коэффициенты, учитывающие влияние шероховатости - коэффициенты, учитывающие влияние шероховатости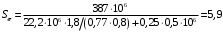 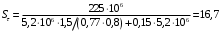 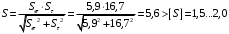 3.8 Проверка тихоходного вала Определяем нормальные напряжения под колесом, концентратор напряжений – шпоночная канавка. 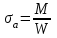 , (39) , (39)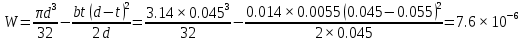 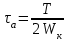 (40) (40) 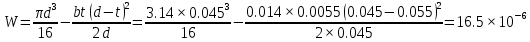 τa=194.2/2×7.6×10-6=5.9 Эффективные коэффициенты концентрации нормальных К и касательных К напряжений 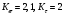 Масштабные факторы для вала d=45 мм по [7, стр. 292]: 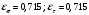 . .Коэффициенты, учитывающие влияние постоянной составляющей цикла для легированных сталей: 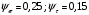 [7, стр. 292]. [7, стр. 292].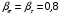 - коэффициенты, учитывающие влияние шероховатости - коэффициенты, учитывающие влияние шероховатости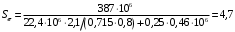 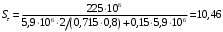 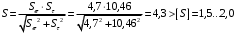 В обоих случаях выносливость валов обеспечена. |
