ким 10 класс. КИМ 10 класс. Параллельность прямых и плоскостей

• Название: Параллельность прямых и плоскостей
• Анкор: ким 10 класс
• Дата: 13.05.2023
• Размер: 1.48 Mb.
• Имя файла: КИМ 10 класс.doc
• Тип: Контрольная работа; #1126840
• страница: 2 из 4

Контрольная работа № 8 «Тригонометрические уравнения»
Вариант 1

Решите уравнения:

1.

2.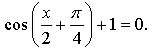

3.

4.

5. Решите уравнение:

6. Найдите корни уравнения принадлежащие отрезку

Вариант 2

Решите уравнения:

1.

2.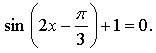

3.

4.

5. Решите уравнение:

6. Найдите корни уравнения принадлежащие отрезку

Решение заданий контрольной работы

Вариант 1

1.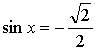



Ответ:

2.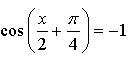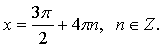









Ответ:

3.





cos х = а

cos х = 1 или cos х = –3

нет решений.

Ответ:

4.





tg x = а



tg x = –1 или



Ответ:

5.







tg x = а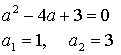



tg x = 1 или tg x = 3



Ответ:

6.

tg 3x = 1





при

при

при

при

при

Ответ: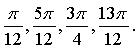

Вариант 2

1.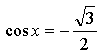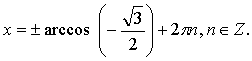





Ответ: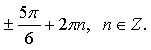

2.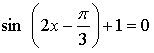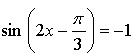









Ответ:

3.





sin х = а

sin х = 1 или sin х = 2

нет решений.

Ответ:

4.





tg x = а



tg x = 1 или



Ответ:

5.







tg x = а

tg x = –1 или tg x = 3



Ответ:

6.





при

при

при

при

при

при

при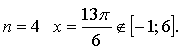

Ответ:

Контрольная работа № 9 «Формулы тригонометрии»

Вариант 1

1. Вычислите.

а)

б)

в)

2. Упростите выражение

3. Решите уравнение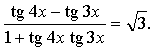

4. Найдите корни уравнения 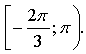принадлежащие полуинтервалу

5. Решите уравнение

6. Докажите, что для любого х справедливо неравенство
Вариант 2

1. Вычислите.

а)

б)

в)

2. Упростите выражение

3. Решите уравнение

4. Найдите корни уравнения принадлежащие промежутку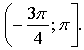

5. Решите уравнение

6. Докажите, что для любого х справедливо неравенство
Критерии оценивания контрольной работы

За успешное выполнение заданий до черты – оценка «3»; за успешное выполнение обязательных заданий и одного дополнительного (после 1-й или 2-й черты) – «4» ; за успешное выполнение заданий всех трех уровней – «5». При этом оценку не рекомендуется снижать за одно неверное решение в первой части (допустимый люфт).

Решение вариантов контрольной работы

Вариант 1

1. а)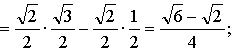



б)

в)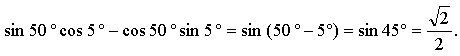

Ответ: а) б) 0; в)

2.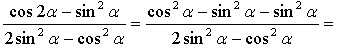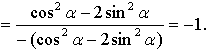



3.







Ответ:

4.







или





Отберем корни, принадлежащие полуинтервалу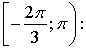



Ответ:

5.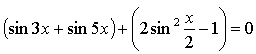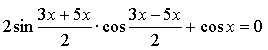









или









Ответ:

6.





– верно, так как аргумент принадлежит II координатной четверти ( 458 °), значит,

Вариант 2

1. а)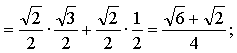



б)

в)

Ответ: а) 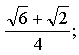б) в) 1.

2.



Ответ:

3.



Ответ:

4.





или





Отберем корни, принадлежащие промежутку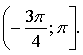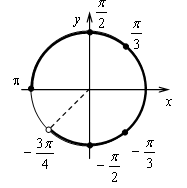



Ответ:

5.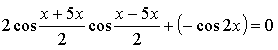









или







Ответ:

6.





– верно, так как аргумент принадлежит III координатной четверти ( 573 °), значит,
Контрольная работа № 10 Тема: Перпендикулярность прямых и плоскостей

Вариант I

1. Диагональ куба равна 6 см. Найдите:

а) ребро куба;

б) косинус угла между диагональю куба и плоскостью одной из его граней.

2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла DABM, М α.

в) Найдите синус угла между плоскостью ромба и плоскостью α.
Вариант II

1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:

а) измерения параллелепипеда;

б) синус угла между диагональю параллелепипеда и плоскостью его основания.

2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.

а) Найдите расстояние от точки С до плоскости α.

б) Покажите на рисунке линейный угол двугранного угла BADM, М α.

в) Найдите синус угла между плоскостью квадрата и плоскостью α.



Контрольная работа № 12 Тема: Многогранники

Вариант I

1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD₁C₁ составляет с плоскостью основания угол в 60°. Найдите:

а) высоту ромба;

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.
Вариант II

1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является параллелограмм ABCD, стороны которого равны а и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:

а) меньшую высоту параллелограмма;

б) угол между плоскостью АВС₁ и плоскостью основания;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.

Ответы